
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интерполяция и аппроксимацияСтр 1 из 2Следующая ⇒ ЛАБОРАТОРНАЯ РАБОТА СРЕДНЕКВАДРАТИЧНОЕ ПРИБЛИЖЕНИЕ ТАБЛИЧНО ЗАДАННЫХ ФУНКЦИЙ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ Цель: Ознакомление студентов с основными методами интерполяции и аппроксимации таблично заданных функций. Закрепление на практике полученных знаний в области аппроксимации таких функций. Задача: Научить студентов практическому применению полученных теоретических знаний при решении задач сглаживания результатов эксперимента полиномами, как при алгоритмизации таких задач, так и при их программировании. ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ Интерполяция и аппроксимация В практике часто встречается ситуация, когда некоторая функция f(x) задана таблицей ее значений в отдельных точках х = x0, x1, … , xn Суть интерполирования – в построении такой легко вычисляемой функции F(x), которая совпадает с функцией f(x) в точках х = x0, x1, … , xn. Иными словами, график функции F(x) в плоскости Оху должен проходить через точки х = x0, x1, … , xn, в которых задана функция f(x). При этом, точки х = x0, x1, … , xn называют узлами интерполирования, а функцию F(x) – интерполяционной. В качестве интерполяционной функции в большинстве случаев выбирают полиномы. Так, линейная интерполяция состоит в простом последовательном соединении точек (x0, f(x0)), (x1, f(x1)), … , (xn, f(xn)) отрезками прямых, т.е. в построении nполиномов первой степени. Значение функции f(x) в точке х*, где х*  f(x*) = f(xi) + Квадратичная интерполяция состоит в соединении последовательных троек узлов интерполяции параболами. Кубическая интерполяция – четверок – кубическими параболами и т.д. Интерполяционные полиномы степени (n – 1)есть гладкие функции, проходящие через все узлы интерполяции. При наложении дополнительных условий на соединение функции F(x)в точках (x1, f(x1)), (x2, f(x2)), … , (xn-1, f(xn-1)) получим т.н. сплайн-интерполяцию. Для построения интерполяционных многочленов разработано множество методов: Ньютона, Стирлинга, Лагранжа и др. Во многих случаях, имея значения функции в n+ 1 узлах, удобно вместо интерполяционного многочлена находить полином степени m<n, который бы хорошо приближал (аппроксимировал) рассматриваемую функцию. При этом требование совпадения функций f(x) иF(x) в точках (x0, f(x0)), (x1, f(x1)), … , (xn, f(xn)) заменяется на требование минимизации суммарного отклонения между значениями функций f(x) и F(x) в точках х = x0, x1, … , xn. Одним из основных методов построения аппроксимизационного полинома является метод наименьших квадратов, по которому требуется, чтобы сумма квадратов отклонений между значениями функции и значениями приближающей функции в узлах должна быть минимальной. Почему квадратов? Потому что сами отклонения между значениями функций может быть как положительными, так и отрицательными, и их сумма не дает истинного представления о различии между функциями за счет компенсации положительныхи отрицательных значений. Можно взять модули отклонений, однако положительные квадраты этих отклонений более удобны в работе. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 294. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
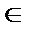 [a, b], например, дискретные показания прибора во времени, а следует вычислить функцию f(x) в некоторых промежуточных точках. Эту задачу можно решить приближенно, заменяя функцию f(x) более простой непрерывной функцией F(x). Существуют два основных способа такой замены: интерполяция и аппроксимация.
[a, b], например, дискретные показания прибора во времени, а следует вычислить функцию f(x) в некоторых промежуточных точках. Эту задачу можно решить приближенно, заменяя функцию f(x) более простой непрерывной функцией F(x). Существуют два основных способа такой замены: интерполяция и аппроксимация.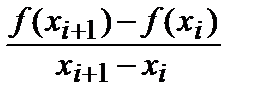 · (х*–xi).
· (х*–xi).