
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Ломаные Эйлера и теорема Пеано. Пусть G – область в
определенное на Доказательство:
◄ Пусть 1. 2. замыкание Такая, что
(в силу открытости G*)
Построим ломаные Эйлера (будем доказывать “вправо”, то есть на Узлы ломаной Эйлера: Уравнения ломаной Эйлера:
где
где Аналогично (см. I семестр) графики ломаных Эйлера при всех
семейство равностепенно непрерывно Придадим h последовательность значений Сделаем оценки:
при
при
и равномерной непрерывности на Аналогично: 
Аналогично прошлому семестру доказывается теорема о продолжении решения в
Теорема о единственности решения задачи Коши для систем ОДУ. Следствие для ОДУ n-го порядка. Случай линейного уравнения и линейной системы. Теорема: Пусть в условии теоремы Пеано функция Доказательство: ◄ Пусть –
По замечанию к лемме Гронуолла:
Следствия для ОДУ n-го порядка. Теорема: Пусть G – область в
определенное в окрестности точки Доказательство: ◄ Для доказательства достаточно перейти к нормальной системе и использовать предыдущие теоремы ►
Следствия для линейной системы. Теорема: Пусть в системе
где
Тогда: 1) 2) 3) определенном на всем Доказательство: ◄ Пусть
По доказанным теоремам существует единственное решение, определенное в окрестности
По замечанию к лемме Гронуолла
при некотором В силу В силу K только при y(x) 0 a b
► Следствия для линейной ОДУ n-го порядка. Теорема: Пусть в уравнении
1) 2) Для любого набора комплексных чисел
3) определенное на всем Доказательство: ◄ Для доказательства достаточно перейти к нормальной линейной системе. ►
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 398. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
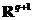 (или в
(или в 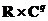 ), а отображение
), а отображение 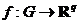 (или
(или 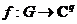 ) непрерывна на G. Тогда
) непрерывна на G. Тогда 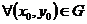
 существует решение задачи Коши:
существует решение задачи Коши: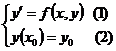
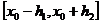 (единственности может не быть).
(единственности может не быть).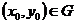 тогда существует область
тогда существует область 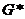 компактно лежащая в G. То есть
компактно лежащая в G. То есть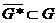
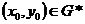 (так как G – открыта, то в качестве
(так как G – открыта, то в качестве  , лежащей в G), то по теореме Вейерштрассе
, лежащей в G), то по теореме Вейерштрассе  ,
, 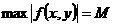 ,
, 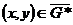 . Поэтому
. Поэтому 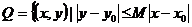 ,
, 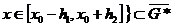 .
.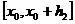 ; “влево” аналогично).
; “влево” аналогично).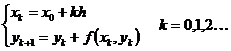
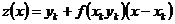 ,
,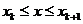 . Как в прошлом семестре, получим, что
. Как в прошлом семестре, получим, что 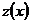 – обобщенное решение задачи Коши:
– обобщенное решение задачи Коши: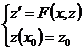 ,
,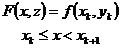 , то есть
, то есть 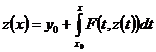 .
.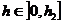 лежат в Q, отсюда следует, что семейство ломаных Эйлера равномерно ограничено при
лежат в Q, отсюда следует, что семейство ломаных Эйлера равномерно ограничено при 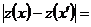
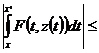

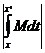 =
= 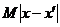

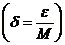 .
.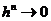
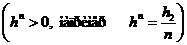 . По лемме Арцелы из соответствующей последовательности ломаных Эйлера
. По лемме Арцелы из соответствующей последовательности ломаных Эйлера 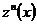 можно выделить равномерно сходящуюся на
можно выделить равномерно сходящуюся на 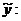
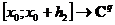 подпоследовательность
подпоследовательность 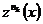 . Покажем, что
. Покажем, что  – решение интегрального уравнения
– решение интегрального уравнения 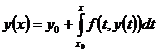 (3). Заметим, что график
(3). Заметим, что график 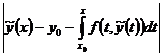

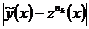 +
+ 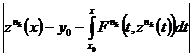 +
+ 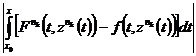 +
+ 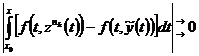
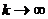 , так как
, так как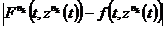 =
= 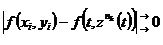 ,
,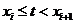 , на
, на 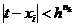 ,
,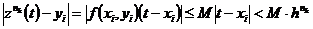
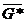 непрерывной функции
непрерывной функции 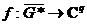 (по теореме Кантора).
(по теореме Кантора).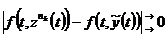 при
при 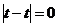 ,
, 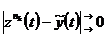 по построению и равномерной непрерывности f на
по построению и равномерной непрерывности f на 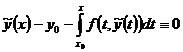
 - окрестности границы области и вплоть до границы области (“липшицевость” не нужна). Как было отмечено выше в теореме Пеано единственности нет.
- окрестности границы области и вплоть до границы области (“липшицевость” не нужна). Как было отмечено выше в теореме Пеано единственности нет. удовлетворяет условию Липшица по y то есть
удовлетворяет условию Липшица по y то есть 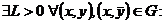
 , тогда решение задачи (1), (2) единственно.
, тогда решение задачи (1), (2) единственно. и
и 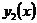 – решения задачи (1), (2) на
– решения задачи (1), (2) на 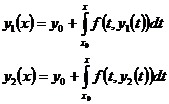
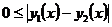 =
= 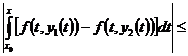
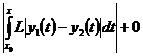 .
.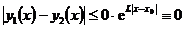
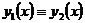 на
на 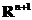 или
или 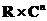 , а функция
, а функция 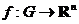
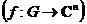 ,
, 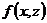 непрерывна по x и удовлетворяет условию Липшица по z, Тогда
непрерывна по x и удовлетворяет условию Липшица по z, Тогда 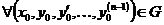 существует единственное решение задачи Коши:
существует единственное решение задачи Коши: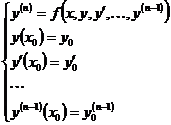 ,
,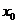 .
.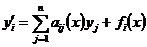 , (1)
, (1)
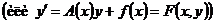 функции
функции  и
и  непрерывны на
непрерывны на 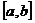 , со значениями в С.
, со значениями в С.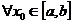 ;
;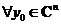
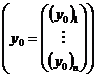 существует единственное решение задачи (1), (2), где
существует единственное решение задачи (1), (2), где 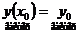 (2);
(2); – произвольный вектор из
– произвольный вектор из 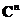 . По теореме Вейерштрассе
. По теореме Вейерштрассе 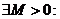
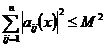 ,
, 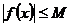 , покажем, что
, покажем, что 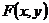 удовлетворяет условию Липшица по y (заметим, что
удовлетворяет условию Липшица по y (заметим, что 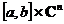 ). Имеем
). Имеем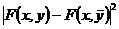 =
= 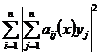
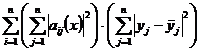
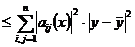
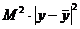
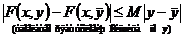 .
. точки
точки 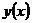 задачи (1), (2):
задачи (1), (2):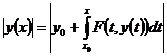 =
= 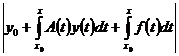
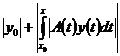 +
+ 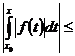
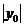 + +
+ + 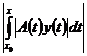 +
+ 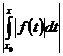
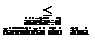
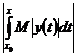 +
+ 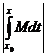
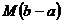
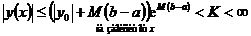
 . Продолжим решение
. Продолжим решение 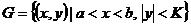 ,
, 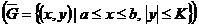 .
. боковой части.
боковой части.
 и при
и при 
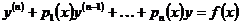 (1).
(1).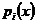 и
и  непрерывны на
непрерывны на 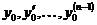
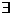 ! решение задачи Коши (1), (2), где
! решение задачи Коши (1), (2), где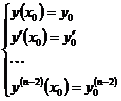 (2),
(2),