
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Правило исследования функции на экстремум1. Найти область определения D функции 2. Найти первые частные производные 3. Определить критические точки из системы 4. Найти все вторые производные, вычислить их в критической точке и составить из них определитель. 5. Сделать заключение на основании теоремы 3. ПРИМЕР 3. Исследовать на экстремум 1. Область определения 2. Первые производные 3. Решим 4. Вторые частные производные
Пусть функция Правило нахождения наибольшего и наименьшего значения 1. Найти первые частные производные, критические точки и экстремумы функции двух переменных. 2. С помощью уравнения границы компакта привести функцию к одной переменной. 3. Найти значение функции во всех критических точках и граничных точках функции одной переменной. 4. Выбрать из них наибольшее и наименьшее значения. ПРИМЕР 4. Для  Заключение Отметим, что: - частные производные задают не только угловые коэффициенты, но и координаты вектора нормали к поверхности в точке; - в точке поверхности будет экстремум, если частные производные =0, т. е. поперечные и продольные касательные горизонтальны; - вторая производная, как и для функции одной переменной, определяет mах, min; - наибольшее, наименьшее значения и mах, min – разные понятия. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель,2001. – 656с.
Цель лекции: изучить понятие двойного интеграла; научиться определять тип задач, приводящих к двойному интегралу; научиться вычислять двойной интеграл. План лекции 1. Задачи, приводящие к понятию двойного интеграла 2. Определение двойного интеграла 3. Свойства двойного интеграла 4. Вычисление двойного интеграла в декартовых координатах Введение Понятие интеграла ранее уже рассматривалось. Напомним, что задачи, связанные с определением первообразной, решаются путем взятия интеграла, то есть это задачи, обратные дифференцированию. Ранее они рассматривались относительно функции одной переменной. Подобные задачи ставятся и для функции многих переменных. В этом случае необходимо вычислять двойной интеграл. Для лучшего понимания двойного интеграла рекомендуется повторить материал трех предыдущих лекций и таблицу интегралов. Понятие двойного интеграла необходимо при изучении темы «Элементы теории поля» и при решении прикладных задач, связанных с определением масс, объемов, средних значений и др. 1. Задачи, приводящие к понятию двойного интеграла 1.1. Объем цилиндрического бруса
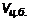 воспользуемся методом предельного перехода при воспользуемся методом предельного перехода при  . Для этого обозначим . Для этого обозначим 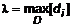 , где за , где за 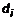 примем расстояние между двумя наиболее удаленными точками границы i-той области. Тогда определим объем как примем расстояние между двумя наиболее удаленными точками границы i-той области. Тогда определим объем как
1.2. Масса неоднородной пластины Дана плоская пластина (рис. 2) с неравномерным распределением плотности. Расположим эту пластину в плоскости
2. Определение двойного интеграла Пусть задана функция
 – подынтегральная функция, – подынтегральная функция,  – элемент площади в декартовой системе координат – элемент площади в декартовой системе координат  . .
Теорема 1 (о существовании двойного интеграла). Если функция 3. Свойства двойного интеграла Двойные интегралы построены по такому же принципу, как и однократные интегралы, то справедливы свойства 1. 2. 3. 4. Если 5. Если 6. 7. Если Теорема 2 (о среднем). Если функция
4.1. Переход к декартовым координатам
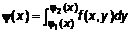 , затем вычисляется внешний интеграл по x, получая число , затем вычисляется внешний интеграл по x, получая число  . Аналогично для . Аналогично для 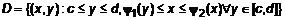 (рис. 5) можно получить (рис. 5) можно получить
Если область определения сложной формы, то ее разбивают на простейшие (рис. 6). Замечание! Внешние пределы всегда постоянные, а внутренние функции переменной, по которой берется внутренний интеграл. Если область определения прямоугольник, то все пределы постоянны (рис. 7).
4.2. Правило вычисления двойного интеграла Чтобы вычислить двойной интеграл, надо привести его к повторному. 1. Для расстановки пределов во внутреннем интеграле надо пересечь область определения D прямой, параллельной координатной оси одноименной с переменной интегрирования, и найти эту переменную из уравнений границ этой области, пересекаемых прямой. 2. Спроецировать область интегрирования на ось, одноименную с переменной внешнего интеграла. Полученный отрезок является интервалом интегрирования внешнего интеграла. ПРИМЕР 1. Определить
Заключение Следует обратить внимание на единую методику при построении интегральных сумм и записи интегралов. Понимание данного материала необходимо для изучения лекции «Тройные интегралы». Важно подробно разобрать последний пример, в котором сведены основные этапы вычисления двойного интеграла, что будет необходимо при изучении следующей лекции, посвященной практическим приложениям двойного интеграла. Особое внимание следует обратить на классификацию области определения подынтегральной функции, так как зачастую неправильный выбор пределов интегрирования существенно затрудняет вычисления. Отметим, что: - двойной интеграл позволяет вычислить объемы тел, не заданных поперечным сечением, а также массу неравномерных пластин; - внутренний интеграл есть функция, определяющая площадь сечения; - область определения функции двух переменных задает пределы интегрирования; - Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов-на-Дону: Феникс, 1997.– 512 с. 3. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. – 656 с. 4. Фихтенгольц Г.М. Основы математического анализа. Часть 2 – М.: Лань, 2002. - 464 с. Лекция 22. Приложения двойного интеграла Цель лекции: научиться использовать известные методы интегрирования при взятии двойных интегралов, уметь применять полученные знания в прикладных задачах. План лекции 1. Замена переменной в двойном интеграле 2. Геометрические приложения двойного интеграла 3. Физические приложения двойного интеграла Введение В предыдущей лекции были даны основные теоретические сведения о двойных интегралах. Они имеют важное значение при решении практических задач. Однако приведенные примеры не в полной мере охватывают области применения кратных интегралов. В этой лекции рассматриваются возможности применения двойного интеграла в прикладных задачах. Будут приведены некоторые новые аналитические выражения, позволяющие решать сложные задачи.
1. Замена переменной в двойном интеграле 1.1. Теорема о переходе к новым переменным Напомним, что правило замены переменной состоит в следующем
Система (1) позволяет заменить элемент площади области
где
 Теорема 1 (о замене переменных). Теорема 1 (о замене переменных).
Если якобиан преобразования не равен нулю
1.2. Переход к полярным координатам
1.3. Вычисление двойного интеграла в полярных координатах Для функции
Если область определения (рис. 3) ограничена двумя непрерывными кривыми
ПРИМЕР 1. Определить
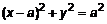 с центром в точке с центром в точке 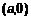 и радиусом и радиусом 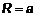 (рис.4). Приведем это уравнение в полярные координаты. Раскроем скобки (рис.4). Приведем это уравнение в полярные координаты. Раскроем скобки 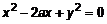 и с учетом правила перехода (см. п. 1.2.) запишем и с учетом правила перехода (см. п. 1.2.) запишем 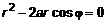 , откуда , откуда 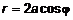 . Аналогично преобразуем подынтегральное выражение и с учетом (2) запишем . Аналогично преобразуем подынтегральное выражение и с учетом (2) запишем 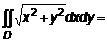 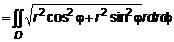 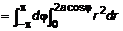 . .
2. Геометрические приложения двойного интеграла 2.1. Объем фигуры
Если фигура снизу ограничена другой поверхностью (рис. 5), то объем образованного тела определяется как разность объемов цилиндров
2.2. Площадь плоской фигуры Если принять
2.3. Площадь криволинейной поверхности Пусть задана гладкая поверхность уравнением
Сравните данное выражение с (2), (3) л. 17.
3.1. Статистические моменты и координаты центра тяжести плоской фигуры
Для нахождения статистических моментов применим интегральный метод. Разобьем пластину на n частей. Обозначим площадь каждой части как
3.2. Моменты инерции Пусть дана плоская пластина (рис. 6) в каждой точке которой задана плотность
ПРИМЕР 2. Пусть пластина, ограниченная областью
Заключение Рассмотрены практические приложения двойного интеграла, необходимые, прежде всего, для решения прикладных задач. Для лучшего усвоения материала предлагается сравнить подходы, используемые в лекции «Приложения определенного интеграла». Понимание общности в решении интегральных задач требуется для изучения следующих лекций, посвященных тройному интегралу, а также при изучении темы «Криволинейные интегралы». Отметим, что: - переход к новым переменным осуществляется с помощью якобиана; - при переходе к новым переменным двойного интеграла, как и при переходе к новой переменной однократного интеграла, необходимо менять пределы интегрирования или, что эквивалентно, изменению области интегрирования; - двойные интегралы, в отличие от простых определенных интегралов, позволяют определить массу, объем и др. более сложных тел; - двойной интеграл позволяет определить площадь любой гладкой криволинейной поверхности, а не только поверхности вращения. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов-на-Дону: Феникс, 1997.– 512 с. 3. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. – 656 с. |
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 209. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
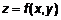 .
.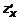 и
и 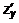 .
.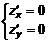 .
.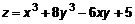 .
.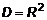 .
. 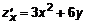 ,
, 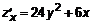 .
. ,
, 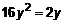 ,
, 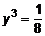 , откуда корни
, откуда корни 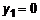 ,
, 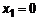 ,
,  ,
, 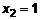 . Две крит. точки P1(0;0) и P2(1;0.5).
. Две крит. точки P1(0;0) и P2(1;0.5).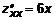 ,
,  ,
, 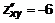 . Рассмотрим первую точку P1(0,0). Составим определитель
. Рассмотрим первую точку P1(0,0). Составим определитель 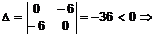 экстремума нет. Рассмотрим вторую точку P2(1,0.5). Составим
экстремума нет. Рассмотрим вторую точку P2(1,0.5). Составим 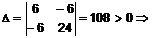 экстремум. Поскольку
экстремум. Поскольку 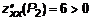 , то это точка минимума.
, то это точка минимума.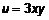 найти наибольшее и наименьшее значение в круге
найти наибольшее и наименьшее значение в круге 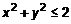 . Определим
. Определим 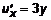 и
и 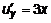 . Составим
. Составим 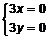 . Одна критическая точка O(0,0). Из уравнения границы выразим
. Одна критическая точка O(0,0). Из уравнения границы выразим 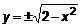 и подставим
и подставим 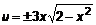 . Это функция двух переменных, заданная на
. Это функция двух переменных, заданная на 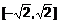 . Определим критические точки
. Определим критические точки 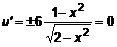 , откуда
, откуда  или
или  . Кроме того,
. Кроме того, 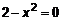 , откуда
, откуда 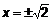 – критические точки на границе компакта. Определим значение функции во всех точках P1(1,1), P2(1,–1), P3(–1,1), P4(–1,–1), P5(
– критические точки на границе компакта. Определим значение функции во всех точках P1(1,1), P2(1,–1), P3(–1,1), P4(–1,–1), P5( 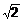 ,0), P6(–
,0), P6(– 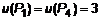 , а наименьшее
, а наименьшее 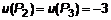 .
. Цилиндрический брус задан снизу областью определения
Цилиндрический брус задан снизу областью определения 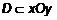 в плоскости
в плоскости  . Сверху ограничен поверхностью
. Сверху ограничен поверхностью  , заданной функцией двух переменных
, заданной функцией двух переменных 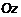 и направляющей – границей области определения
и направляющей – границей области определения 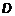 (рис. 1). Задача – найти объем цилиндрического бруса
(рис. 1). Задача – найти объем цилиндрического бруса  . Выберем i-тую часть. Из точек контура этой части проведем прямые
. Выберем i-тую часть. Из точек контура этой части проведем прямые  до пересечения с
до пересечения с 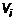 . Возьмем произвольную точку
. Возьмем произвольную точку 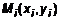 из основания
из основания 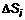 . Обозначим высоту этого бруса
. Обозначим высоту этого бруса  . Объем i-того бруса
. Объем i-того бруса 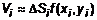 . Аналогично найдем остальные
. Аналогично найдем остальные 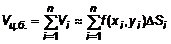 . (1)
. (1)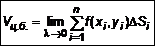 . (1)
. (1) . Если масса пластины
. Если масса пластины  , то масса пластины определяется через ее площадь
, то масса пластины определяется через ее площадь 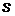 как
как 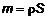 . Разобьем пластину на n частей. Обозначим площадь i-той части как
. Разобьем пластину на n частей. Обозначим площадь i-той части как  из основания
из основания  . Если принять ее постоянной в пределах элементарной части, то масса i-го участка равна
. Если принять ее постоянной в пределах элементарной части, то масса i-го участка равна 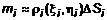 . Тогда масса всей пластины
. Тогда масса всей пластины 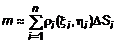 . Аналогично предыдущей задаче используем метод предельного перехода, при этом получим точное значение массы
. Аналогично предыдущей задаче используем метод предельного перехода, при этом получим точное значение массы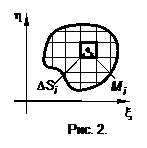
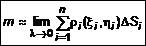 . (2)
. (2)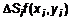 . Составим интегральную сумму произведений
. Составим интегральную сумму произведений 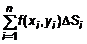 . Найдем предел суммы при
. Найдем предел суммы при  , где
, где 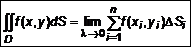 , (3)
, (3)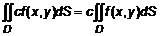 .
.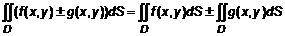 .
.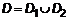 и
и 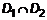 =
= 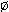
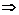
 .
.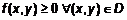 , то
, то 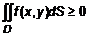 .
.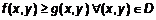 , то
, то 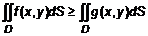 .
. .
.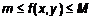 , то
, то  , где S – пл. D.
, где S – пл. D. , такая что
, такая что 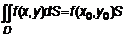 , где
, где 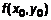 – среднее значение функции в D
– среднее значение функции в D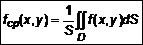 . (4)
. (4)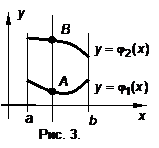 Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.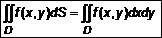 . (5)
. (5) Объем
Объем  (рис. 3). Здесь
(рис. 3). Здесь 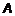 – вход,
– вход, 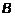 – выход,
– выход, 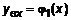 ,
, 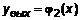 . На рис. 4 изображен цилиндрический брус. Для фиксированного значения переменной
. На рис. 4 изображен цилиндрический брус. Для фиксированного значения переменной 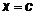 получим в сечении этого бруса криволинейную трапецию
получим в сечении этого бруса криволинейную трапецию 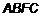 , ограниченную сверху кривой
, ограниченную сверху кривой 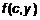 , а снизу – отрезком
, а снизу – отрезком 
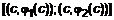 . Очевидно, что площадь этой трапеции определяется интегралом
. Очевидно, что площадь этой трапеции определяется интегралом 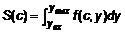 . Для произвольного сечения
. Для произвольного сечения  его площадь
его площадь 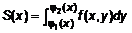 . Тогда
. Тогда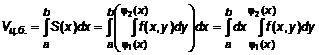 . (6)
. (6)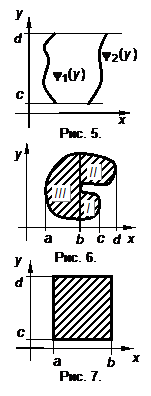 Сравнивая это выражение с (3), запишем
Сравнивая это выражение с (3), запишем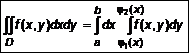 . (7)
. (7)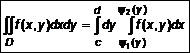 . (7)
. (7)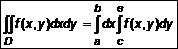 . (8)
. (8)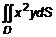 , если область определения
, если область определения
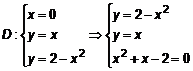 .
.
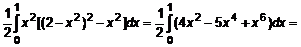
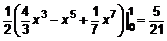 .
.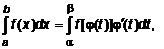
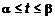 . Пусть при вычислении двойного интеграла потребовалась замена переменной по системе
. Пусть при вычислении двойного интеграла потребовалась замена переменной по системе
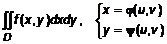 . (1)
. (1) ,
,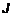 – якобиан преобразования
– якобиан преобразования 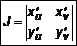 , то есть происходит переход от одной области определения к другой (рис. 1).
, то есть происходит переход от одной области определения к другой (рис. 1).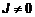 для любых
для любых 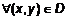 , то справедливо преобразование
, то справедливо преобразование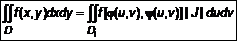 . (1)
. (1)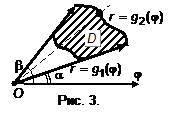 Переход к полярным координатам осуществляется по формулам
Переход к полярным координатам осуществляется по формулам 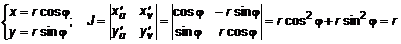 . Подставляя последнее в (1), получим
. Подставляя последнее в (1), получим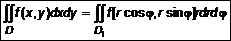 . (2)
. (2)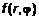 задана область определения, ограниченная двумя лучами
задана область определения, ограниченная двумя лучами  ,
,  ,
,  и непрерывной кривой
и непрерывной кривой 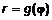 (рис. 2), где r и
(рис. 2), где r и  - полярные координаты точек кривой (см. л. 17). Поскольку область D уже задана в полярных координатах, то нет необходимости применять (2), и двойной интеграл будет иметь вид
- полярные координаты точек кривой (см. л. 17). Поскольку область D уже задана в полярных координатах, то нет необходимости применять (2), и двойной интеграл будет иметь вид
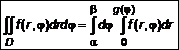 . (3)
. (3)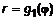 и
и 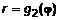 , то выражение (3) примет вид
, то выражение (3) примет вид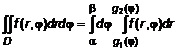 .
.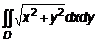 , если
, если 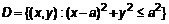 .
.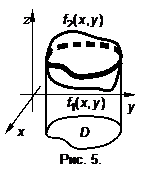 Объем цилиндрического бруса задан снизу областью определения
Объем цилиндрического бруса задан снизу областью определения 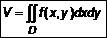 .
.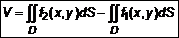 .
.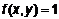 , т. е. если задан плоский цилиндр с единичной высотой, то его объем будет равен площади его основания
, т. е. если задан плоский цилиндр с единичной высотой, то его объем будет равен площади его основания  . (4)
. (4)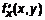 и
и 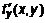 непрерывны. Определим площадь этой поверхности. Применим интегральный метод, разбивая поверхность на участки. Вычисляем площадь каждого участка, заменяя его касательной плоскостью. Далее перейдем к пределу интегральной суммы и получим
непрерывны. Определим площадь этой поверхности. Применим интегральный метод, разбивая поверхность на участки. Вычисляем площадь каждого участка, заменяя его касательной плоскостью. Далее перейдем к пределу интегральной суммы и получим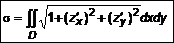 . (5)
. (5) Пусть дана плоская пластина (рис. 6), в каждой точке которой задана плотность
Пусть дана плоская пластина (рис. 6), в каждой точке которой задана плотность  определяются согласно выражениям
определяются согласно выражениям  ,
,  . Очевидно, что масса пластины
. Очевидно, что масса пластины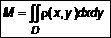 . (6)
. (6) . В i-ой части выберем произвольно точку
. В i-ой части выберем произвольно точку 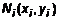 . Предположим, что в этой части плотность постоянна
. Предположим, что в этой части плотность постоянна 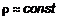 и масса сосредоточена в одной точке
и масса сосредоточена в одной точке 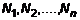 будут определяться согласно
будут определяться согласно , откуда
, откуда 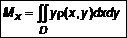 ; (7)
; (7)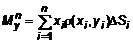 , откуда
, откуда 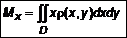 . (8)
. (8)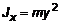 ,
,  ,
, 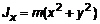 .
.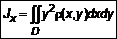 ,
, 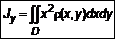 ,
, 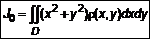 . (9)
. (9) (рис. 7), имеет неравномерную плотность
(рис. 7), имеет неравномерную плотность 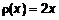 . Определим момент
. Определим момент 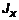 :
: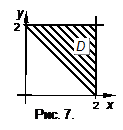

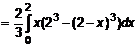 .
.