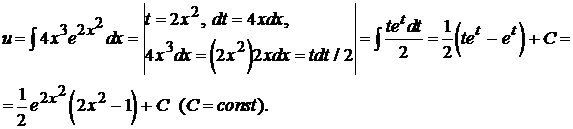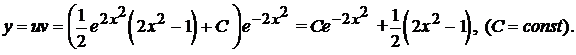Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод двух множителей БернуллиОбщее решение уравнения (5.2) ищем в виде произведения двух функций
где Учитывая, что
Подберем функцию
Первое уравнение – дифференциальное уравнение с разделяющимися переменными относительно функции
Найдя функцию
Замечание 2. Итак, показано, как найти общее решение ЛДУ-I методом Бернулли. Заметим, что ЛДУ-I обязательно имеет общее решение (так как две функции последовательно выражаются через неопределенные интегралы от непрерывных функций). Однако на практике бывают такие случаи, что нельзя вычислить конечным числом операций получающиеся неопределенные интегралы.  Пример 1. Найти методом Бернулли общее решение ЛДУ-I
Решение: В данном случае
Первое уравнение системы (5.7) дает
Теперь знание функции v=v(x) (заметим, что здесь мы нашли явную зависимость v от x) поможет нам определить функцию u=u(x). Подставляя во второе уравнение системы (5.7) функцию
Неопределенный интеграл
Итак, общее решение ЛДУ-I имеет вид
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 229. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
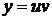 , (5.3)
, (5.3)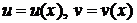 – неизвестные функции, причем одну из них выберем произвольно, а другую определенным образом. Заметим, что уравнение (5.2), как и уравнение (5.1) не имеет (тривиального) нулевого решения, то есть функции u, v не равны тождественно нулю.
– неизвестные функции, причем одну из них выберем произвольно, а другую определенным образом. Заметим, что уравнение (5.2), как и уравнение (5.1) не имеет (тривиального) нулевого решения, то есть функции u, v не равны тождественно нулю.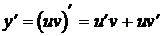 (
( 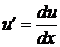 ,
, 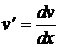 ). Предполагая, что функция (5.3) должна являться решением уравнения (5.2), подставим выражения для
). Предполагая, что функция (5.3) должна являться решением уравнения (5.2), подставим выражения для 
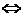
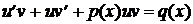
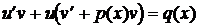 .
.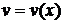 таким образом, чтобы выражение, стоящее в скобках обнулилось:
таким образом, чтобы выражение, стоящее в скобках обнулилось: 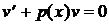 ; при этом получим второе уравнение
; при этом получим второе уравнение 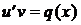 для нахождения другой функции
для нахождения другой функции 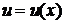 . Итак, получаем систему
. Итак, получаем систему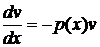
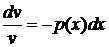
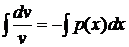
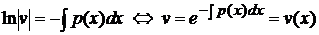 (так как функцию
(так как функцию 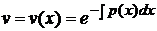 .
.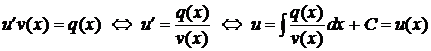 . Используя равенство (5.5), получаем общее решение уравнения в виде
. Используя равенство (5.5), получаем общее решение уравнения в виде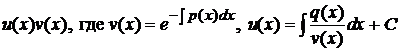 (C=const). (5.6)
(C=const). (5.6)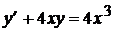 .
.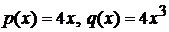 (обе функции непрерывны на всей числовой оси). Можно, конечно, сразу использовать формулу (5.6), подставив в нее исходные данные, но обычно это не делается, а просто применяется сама методика решения задачи. Ищем решение в виде (5.3). Получаем
(обе функции непрерывны на всей числовой оси). Можно, конечно, сразу использовать формулу (5.6), подставив в нее исходные данные, но обычно это не делается, а просто применяется сама методика решения задачи. Ищем решение в виде (5.3). Получаем (5.7)
(5.7)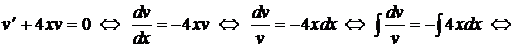
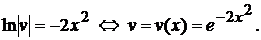
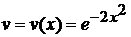 , получим
, получим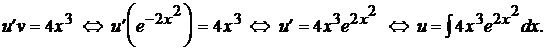
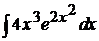 вычисляется сначала заменой
вычисляется сначала заменой 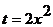 , а затем интегрированием по частям
, а затем интегрированием по частям