Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Первого порядка. Метод изоклинПриведем формулировку основной теоремы для обыкновенного дифференциального уравнения первого порядка вида
Теорема Коши (о существовании и единственности решения). Если функции
Геометрически данная теорема утверждает следующее: если функции Пусть далее для уравнения (2.1) выполняются условия теоремы Коши в некоторой области
Тогда задачу нахождения решения уравнения (2.1) геометрически можно сформулировать следующим образом: найти интегральную кривую, удовлетворяющую условию, что касательные к ней имеют направления, совпадающие с направлением поля в точках касания.  Одним из методов решения такой задачи является метод изоклин. Изоклиной (линией равного наклона) называется геометрическое место точек с одинаковым направлением поля (одинаковым углом наклона
Чтобы применить метод изоклин, поступают следующим образом. Находят уравнения семейства изоклин, используя равенство (2.4) (желательно это сделать в явном виде – как зависимость y от x). Придавая в равенстве (2.4) константе C различные значения ( Пример 2.1. С помощью метода изоклин построить интегральные кривые дифференциального уравнения . Сравнить с точным решением. Решение: Определяем семейство изоклин, учитывая равенство (2.4), где Теперь будем придавать константе C различные числовые значения и составлять уравнения изоклин. Оформим этот процесс в виде таблицы.
Изображаем на координатной плоскости Рис.2.3.
Сравним полученные интегральные кривые с кривыми, которые определяют точное решение исходного уравнения. Общее решение уравнения имеет вид 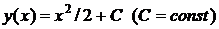 . Замечаем, что на координатной плоскости . Замечаем, что на координатной плоскости 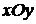 они также представляют собой семейство парабол. они также представляют собой семейство парабол.
Лекция 2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 543. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
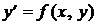 . (2.1)
. (2.1) ,
, 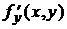 непрерывны в некоторой области
непрерывны в некоторой области 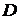 переменных
переменных  , то при любых начальных условиях
, то при любых начальных условиях 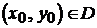 существует единственное решение
существует единственное решение  уравнения (2.1), удовлетворяющее условию
уравнения (2.1), удовлетворяющее условию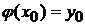 . (2.2)
. (2.2)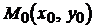 этой области будет проходить единственная интегральная кривая уравнения (2.1).
этой области будет проходить единственная интегральная кривая уравнения (2.1).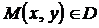 значение функции
значение функции 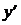 , то есть величине углового коэффициента касательной к интегральной кривой, проходящей через эту точку:
, то есть величине углового коэффициента касательной к интегральной кривой, проходящей через эту точку: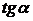 ,
, – угол наклона касательной к оси Ox.
Графически это можно изобразить прямолинейной стрелкой (
– угол наклона касательной к оси Ox.
Графически это можно изобразить прямолинейной стрелкой (  ), проходящей через точку
), проходящей через точку  . (2.3)
Аналитически говорят, что в области
. (2.3)
Аналитически говорят, что в области 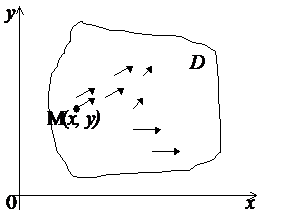 Рис. 2.1
Рис. 2.1
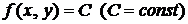 . (2.4)
. (2.4) различные значения, получим семейство (множество) изоклин. Во всех точках изоклины, соответствующей некоторому фиксированному значению константы
различные значения, получим семейство (множество) изоклин. Во всех точках изоклины, соответствующей некоторому фиксированному значению константы 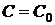 , касательные к интегральным кривым имеют одинаковое направление, т. е. наклонены под одним и тем же углом
, касательные к интегральным кривым имеют одинаковое направление, т. е. наклонены под одним и тем же углом 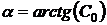 (см. рис. 2.2).
(см. рис. 2.2).
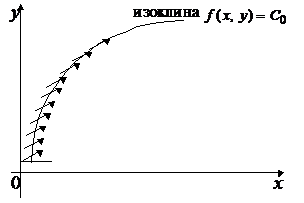 Рис.2.2
Рис.2.2
 . Изоклинами в нашем случае будут являться вертикальные прямые
. Изоклинами в нашем случае будут являться вертикальные прямые 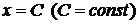 .
.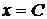 , соответствующее значению
, соответствующее значению 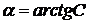 (в градусах)
(в градусах)
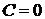
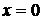
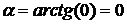

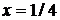
 (1/4)
(1/4)  16
16 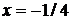
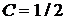
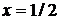
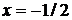

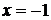
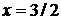
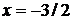
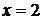
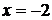
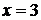
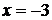
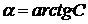 (см. рис.2.3). Замечаем, что нанесенные штрихи качественно определяют (восстанавливают) расположение интегральных кривых для дифференциального уравнения. Эти интегральные кривые параболы.
(см. рис.2.3). Замечаем, что нанесенные штрихи качественно определяют (восстанавливают) расположение интегральных кривых для дифференциального уравнения. Эти интегральные кривые параболы.