
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Необходимый и достаточный признаки локального экстремума.Теорема Ферма. Если функция имеет локальный экстремум в точке Необходимое условие экстремума: Если точка Доказательство По условию точка
Первое достаточное условие экстремума в терминах первой производно: Пусть функция Если производная Если производная
Второе достаточное условие строгого экстремума в терминах второй производной: Пусть дана функция Если Если
Третье достаточное условие строгого экстремума в терминах производных порядка больше двух: Пусть функция 1. Если · если · если 2. Если
Наибольшее и наименьшее значение функции на отрезке. Если функция  Если свое наибольшее значение Наименьшим значением
Выпуклость, вогнутость кривой. Точки перегиба кривой. График функции График функции Точкой перегиба графика функции
Асимптоты графика функции. 1. Прямая · Замечание. Прямая
2. Прямая · Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
3. Прямая Нахождение наклонной асимптоты Теорема. Если для функции
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 270. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
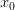 и дифференцируема в этой точке, то
и дифференцируема в этой точке, то 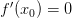 .
.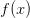 , то она критическая.
, то она критическая.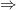 по теореме Ферма производная
по теореме Ферма производная 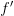 меняет знак с «-» на «+» при переходе через точку
меняет знак с «-» на «+» при переходе через точку 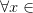
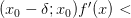
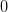 и
и 
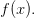
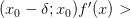

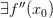 , тогда:
, тогда: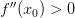 , то точка
, то точка 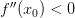 , то точка
, то точка 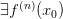 ,
, 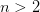 и
и 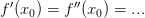
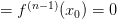 ,
, 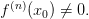 Тогда:
Тогда: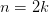 (т.е
(т.е 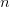 — четное), то
— четное), то  , то
, то 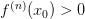 , то
, то 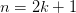 (т.е
(т.е 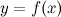 определена и непрерывна на отрезке
определена и непрерывна на отрезке 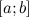 , то она на этом отрезке достигает своих наибольшего и наименьшего значений.
, то она на этом отрезке достигает своих наибольшего и наименьшего значений.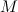 функция
функция 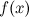 принимает в точке
принимает в точке 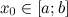 , то
, то 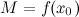 будет локальным максимумом функции
будет локальным максимумом функции 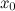 , такая, что
, такая, что 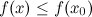 . Чтобы найти наибольшее значение
. Чтобы найти наибольшее значение 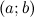 и значения
и значения  и
и 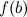 , и выбрать среди них наибольшее.
, и выбрать среди них наибольшее. непрерывной на отрезке
непрерывной на отрезке 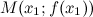 , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости. называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 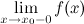 или
или 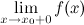 равно
равно 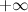 или
или 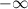 .
.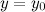 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 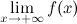 или
или 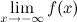 равно
равно 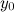 .
. называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 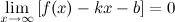
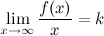 и
и 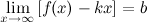 , то функция имеет наклонную асимптоту
, то функция имеет наклонную асимптоту 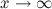 .
.