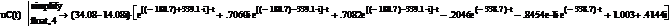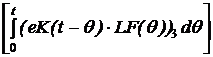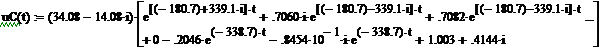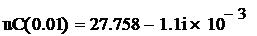Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Переходные процессы при мгновенном изменении реактив-ных параметров участков цепи (при «некорректных» коммутациях) ⇐ ПредыдущаяСтр 3 из 3 При рассмотрении переходных процессов в цепях с размыканием ветвей, содержащих индуктивности, или при включении заряженных конден- саторов параллельно токи в индуктивных элементах или напряжения на ёмкостных элементах теоретически могут измениться скачком во время ком-мутации, что означает нарушение законов коммутации в ранее принятом виде. Такие результаты – итог предельной идеализации явления. В действитель-ности большие напряжения между контактами ключа вызовут электрическую искру или дугу. Кроме того, не учитываются сопротивления проводов и контактов соединений, наличие распределённой ёмкости между витками катушки. Разность энергий W(0-) – W(0+) расходуется в неучтённых сопро-тивлениях цепи и на излучение при весьма высокой частоте. Уточнённые законы коммутации формулируются следующим образом. Первый обобщенный закон коммутации. Потокосцепление любого замкнутого контура в момент коммутации (t = 0+) равно алгебраической сумме потокосцеплений всех входящих в него катушек, которые последние имели непосредственно до коммутации (t = 0-). Некоторые из этих катушек перед коммутацией могли одного замкнутого контура и не составлять, а образовали его лишь после коммутации. Второй обобщенный закон коммутации. Изменение зарядов на всех параллельно включенных конденсаторах за время коммутации равно нулю. То есть сумма зарядов конденсаторов перед коммутацией (t = 0-) равна сумме зарядов непосредственно после коммутации (t = 0+).
Решение Токи до коммутации:  i2(t–)= 0, i1(t–)= Уравнение по второму закону Кирхгофа для вторичного контура -M Ввиду скачкообразного изменения первичного тока с 10 А до 0 производные i1 – от i1(0–) = 10 А до i1(0+) = 0, i2 – от i2(0–) = 0 до искомого i2(0+). L2 Отсюда i2(0+) = - Постоянная времени цепи t = Корень характеристического уравнения р = -t -1= -20 с -1. Ток переходного процесса i2(t) = i2(0)×е рt = -10×е -20t А. Знак «минус» у тока означает его обратное направление на схеме.
ЗАДАЧА 7.36. Рассчитать ток первой катушки в схеме рис. 7.55 со следующими числовыми данными: U = 100 В, r1 = 60 Ом, r2 = 40 Ом, L1= 0,1 Гн, L2= 0,2 Гн, М = 0,05 Гн. Построить график то-ка в первой катушке. Решение 1. До коммутации в катушках были разные токи: в первой катушке – i1(0-) = Таким образом, потокосцепление цепи до коммутации, состоящее из суммы потокосцеплений катушек Y(0-) = Y1(0-) + Y2(0-) = L1i1(0-) + Мi2(0-) + L2i2(0-) + Мi1(0-) = = 0,1×1,667 + 0 + 0 + 0,05×1,667 = 0,25 Вб. Независимое начальное условие в соответствии с первым законом коммутации: Y(0+) = Y(0-) = 0,25 Вб. Но потокосцепление цепи после комму-тации с учётом того, что катушки соединены последовательно согласно и по ним протекает один ток, равно Y(0+) = i(0+)×(L1 + L2 + 2М). Отсюда i(0) = 2. Принуждённая составляющая тока: iпр = 3. Характеристическое уравнение: р×(L1 + L2 + 2М) + r1 + r2 = 0, р = -
iсв = А×е рt, где постоянная интегрирования А = iсв(0) = i(0) – iпр = 0,625 – 1 = -0,375. 5. Окончательно получаем: i(t) = iпр(t) + iсв(t) = 1 – 0,375×е –250t А. 6. График тока приведен на рис. 7.56.
Решение 1. До коммутации r = r + i1(0-) = i2(0-) = 2. Уравнение для контура со второй катушкой по второму закону Кирхгофа для момента коммутации: r×(i1 + i2) + r2×i2 + L2 или L2×(i2(0+) – i2(0-)) =-M×(i1(0+) – i1(0-)). Но i1(0+) = 0, тогда i2(0+) = 3. Принуждённая составляющая тока i2пр = 4. Корень характеристического уравнения р = - 5. Свободная составляющая тока i2св = А×е рt, где постоянная интегрирования А = i2св(0) = i2(0) – i2пр = 1,65 – 0,975 = 0,675. 6. Окончательно получаем: i2(t) = i2пр(t) + i2св(t) = 0,975 + 0,675×е –600t А.
ЗАДАЧА 7.38. Рассчитать переходный ток i1(t) в схеме рис. 7.58 со следующими числовыми данными: Е1= 36 В, Е2= 6 В, r1 = 300 Ом, r2 = r3 = 600 Ом, С1= 300 мкФ, С2= 200 мкФ. Решение До коммутации напряжения и суммарный заряд конденсаторов: uС1(0-) = q(0-) = С1uС1(0-) + С2uС2(0-) = (300×24 – 200×6)×10 -6 = 60×10 -4 Кл. После коммутации конденсаторы будут находиться под одним напряжением uС(0+) = uС1(0+) = uС2(0+). Поэтому заряд конденсаторов после коммутации q(0+) = (С1 + С2)×uС(0+). Но в соответствии со вторым законом коммутации q(0+) = q(0-). Отсюда uС(0+) = Начальное значение искомого тока i1(0) = Принуждённый ток i1пр= Свободный ток i1св = А×е рt, где корень характеристического уравнения р = - постоянная интегрирования А = i1св(0) = i1(0) – i1пр = 80 – 40 = 40. Окончательно записываем: i1(t) = i1пр(t) + i1св(t) = 40 + 40×е –10t мА.
С1= 1 мкФ, С2= 2 мкФ. Ответы: uС1(0+) = uС2(0+) = 20 В, i(t) = 30 + 10×е –667t мА. 7.1.5. Метод переменных состояния(МПС) Уравнениями состояния можно назвать любую систему уравнений, определяющих режим цепи. В более узком смысле – это система дифференциальных уравнений первого порядка, разрешённая относительно производных. МПС – анализ цепи, основанный на решении уравнений состояния, записанных в форме Коши. В электрических цепях токи в индуктивностях и напряжения на ёмкостях определяют энергетическое состояние цепи, поэтому их целесообразно взять в качестве переменных состояния – xk(t): [X] – матрица-столбец (размера k) переменных состояния. Действующие источники называются входными величинами – Fl(t): [F] – матрица-столбец (размера l) ЭДС и токов источников (внешних возмущений); искомые величины (остальные токи и напряжения) – выходные величины Wm(t): [W] – матрица-столбец размера m. Сокращённо дифуравнения состояния записываются в матричной форме: где [K] – квадратная матрица порядка k (основная), [L] – матрица связи разме-ра k´l. Элементы этих матриц определяются топологией и параметрами цепи. Для выходных величин: [W] = [M]´[X] + [N]´[F], где [M]– матрица связи размера m´k, [N]– матрица связи размера m´l. Согласно классическому методу токи и напряжения находятся в виде суммы принуждённых и свободных составляющих: iL(t) = iLпр(t) + iLсв(t); uC(t) = uCпр(t) + uCсв(t). Методика определения принуждённых составляющих следующая: - если источники постоянные, то производные от принуждённых составляющих равны нулю: - если источники синусоидальные – удобно перейти к комплексам: jw[Xnp] = [K]´[Xnp] + [L]´[F]. Система уравнений даёт возможность удобно составить характеристическое уравнение. Для этого систему нужно алгебраизировать и её определитель, состоящий из коэффициентов при переменных состояния, приравнять к нулю. Составлять характеристическое уравнение через входное сопротивление в операторной форме целесообразно лишь в цепочных схемах, где нет мостиковых соединений ветвей и индуктивных связей. Непосредственно из системы уравнений можно получить начальные значения производных от переменных состояния, подставив в систему независимые начальные условия. Эти начальные значения используются при нахождении постоянных интегрирования. Система уравнений состояния может также решаться матричным способом с помощью программируемой вычислительной техники. Примеры – см. задачи 7.43 и 7.44. ЗАДАЧА 7.40. Рассчитать токи переходного процесса в схеме рис. 7.60 методом переменных состояния. Числовые значения: Е = 100 В, J = 5 A, r1 = 20 Ом, r2 = 30 Ом, r3 = 10 Ом, L = 0,09 Гн, C = 100 мкФ.
1. Назначаем в каче-стве переменных состояния ток в индуктивности и напряжение на конденсато-ре – i1(t) и uC(t). Выходные переменные – остальные токи: i2(t), i3(t), i4(t).
i1(0+) = i1(0-) = uC(0+) = uC(0-) = J×r3 = 5×10 = 50 В. 3. Для переменных состоя-ния составим систему дифферен-циальных уравнений в форме Коши. Производные i1¢(t) и uC¢(t) получим, соответственно, из uL = Li1¢(t) и i4= CuC¢(t). Для нахождения uL и i4в исходной схеме заменим индуктивность источником тока i1, а емкость – источником напряжения uC. В резистивной цепи рис. 7.61 определим uL и i4, а также выходные переменные i3(t) и i2(t). Это можно сделать любым методом расчёта сложных цепей постоянного тока. выполним расчёт методом контурных токов. Имеем три независимых контура с двумя известными токами i1 и J и с одним неизвестным i3. Составляем одно уравнение: (r2+ r3)×i3+ r2×i1 = uC. Решение уравнения: i3= Остальные расчётные величины: i2 = i1 + i3 = i4 = С uL = L Из последних двух уравнений получаем уравнения состояния в форме Коши:
Остальные полученные уравнения называются уравнениями связи. Они нужны для нахождения выходных переменных. 4. Систему уравнений состояния решим классическим методом: i1(t)= i1пр(t) + i1св(t); uC (t)= uCпр(t) + uCсв(t). Поскольку в цепи действуют постоянные источники, принуждённые составляющие являются также постоянными, а производные от них равны нулю. В соответствии с принципом наложения система уравнений состояния оказывается справедливой не только для полных i1(t) и uC (t), но и для их составляющих. Система уравнений состояния для принуждённых составляющих, таким образом, имеет вид:
Решение системы: i1пр = -1 А, uCпр = 170 В. 5. Алгебраизировав уравнения состояния и приравняв определитель системы уравнений к нулю, получим характеристическое уравнение: D(р) = = р2 + Корни характеристического уравнения: р1,2 = -277,8 ± j248,5 с -1. Свободные составляющие имеют вид: i1св(t) = А×е -a×t×sin(wt +Y1); uCсв(t) = B×е -a×t×sin(wt +Yu), Здесь a = |Re(р1)| = -277,8 с –1 – коэффициент затухания, w = Im(р1) = 248,5 с –1 – угловая частота свободных колебаний. Начальные значения свободных составляющих и их производных: i1св(0) = А×sinY1; i1св¢ (0) = -a ×А×sinY1 + w ×А×cosY1; uCсв(0) = B×sinYu; uCсв¢ (0) = -a ×B×sinYu + w ×B×cosYu. 6. Независимые начальные условия: i1(0) = 5 А, uC(0) = 50 В. Начальные значения производных получим из уравнений состояния: i1¢(0) = - = - uC¢(0) = = 0,75×10 4×5 – 0,025×10 4×50 + 10 4×5 = 75000 В/с. Начальные значения свободных составляющих и их производных: i1св(0) = i1(0) – i1пр = 5 + 1 = 6 А, i1св¢(0) = i1¢(0) – i1пр¢ = -833,3 А/с, uCсв(0) = uC(0) – uCпр = 50 – 170 = -120 В, uCсв¢(0) = uC¢(0) – uCпр¢= 75000 В/с. Получаем и решаем следующие системы уравнений:
-a ×А×sinY1 + w ×А×cosY1 = -833,3; -a ×B×sinYu + w ×B×cosYu = 75000. А = 6,874, Y1 = 60,8°, B = 452,1, Yu = -15,4°. 7. Окончательные выражения для переменных состояния: i1(t)= i1пр(t) + i1св(t) = -1 + 6,874×е –277,8t×sin(248,5t + 60,8°) А; uC (t)= uCпр(t) + uCсв(t) = 170+ 452,1×е –277,8t×sin(248,5t – 15,4°) В. 8. Выходные переменные: i2(t) = = 4 + 11,83×е –277,8t×sin(248,5t – 7,29°) А; i3(t) = = 5 + 11,25×е –277,8t×sin(248,5t – 41,83°) А; i4(t) =
ЗАДАЧА7.41. Рассчитать токи пере-ходного процесса, напряжения на индук-тивности и ёмкости в цепи рис. 7.62, если Е = 240 В, J = 4 A, r1 = 80 Ом, r2 = 120 Ом, r3 = 120 Ом, L = 0,5 Гн, C = 10 мкФ. Ответы: uC(t)= 200 + 126,3×е –140t×sin(424,7t + 71,75°) B; i1(t) = 4 – 0,565×е –140t×sin(424,7t) А; i2(t) = 1 – 0,283×е –140t×sin(424,7t) А; i3(t) = 1 + 0,283×е –140t×sin(424,7t) А; iC(t) = -0,565×е –140t×sin(424,7t) А; uL(t)= 120,1×е–140t×sin(424,7t + 92,7°) B.
ЗАДАЧА7.42. Определить токи переходного процесса в цепи рис. 7.63, если r1 = r4 = 200 Ом, r2 = r5 = 100 Ом, C1 = C3 = 100 мкФ, Е = 300 В, J = 1 A. Ответы:
i2(t) = 1 – 0,8×е –16,67t + 0,3×е –100t А; i3(t) = 0,4×е –16,67t + 0,6×е –100t А; i4(t) = -1 + 1,2×е –16,67t + 0,3×е –100t А.
ЗАДАЧА 7.43. Построить графики токов i1(t) и i3(t) схемы рис. 7.64, при условии r1 = 60 Ом, r2 = 40 Ом, C = 100 мкФ, L = 0,1 Гн, u = 100 В. Решение Задачу решим МПС матричным способом. В этом случае целесообразно использовать программируемую вычислительную технику. Решим задачу в среде MathCAD. 1. Назначаем в качестве переменных состояния ток в индуктивности и напряжение на конденсаторе – i3(t) и uC(t). Выходная переменная – ток i1(t). 2. Независимые начальные условия нулевые: i3(0+) = i3(0-) = 0, uC(0+) = uC(0-) = 0. 3. Составим систему уравнений состояния, используя законы Кирхгофа: L Таким образом, система уравнений состояния имеет вид:
Эта же система в матричном виде: Итак, матрица переменных состояния [X], матрица коэффициентов [K], столбцовая матрица свободных членов [L]´[F] и матрица независимых начальных условий [X(0)] имеют вид: [X] = Решение системы уравнений состояния: X(t)= eKt·Ф(t), где Ф(t) = X(t)= eKt = eKt·X(0) + eKt
4. Получим матричную экспоненциальную функцию eKt. Сначала определим собственные значения l матрицы [K], то есть корни уравнения det([K]– l·1) = 0, где 1= Е– единичная матрица порядка K:
В данном случае характеристическое уравнение: При двух корнях характеристического уравнения матричная экспонента находится в виде eKt = a0 Е + a1[K], где коэффициенты ai находят из следующей системы уравнений:
a0 + l2 a1 = el2·t. a1 = 5. Далее переменные состояния можно найти по формуле (**), а выходную переменную i1(t) по формуле i1 = 6. Ниже приводится программа расчётов в среде MathCAD с построенными графиками i1(t) и i3(t). j:= E:= |K - l·E| |K - l·E| = 0 Перезадание корней характеристического уравнения l:=
a0(t):= 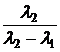 · · 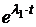 + + 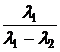 · · 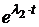 a1(t):= a1(t):= 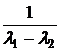 · · 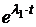 + + 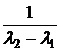 · · 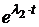
eK(t):= a0(t)·E + a1(t)·K i3(t):= (eK(t)·x0)1 + 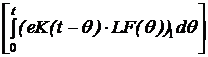
uC(t):= (eK(t)·x0)2 +
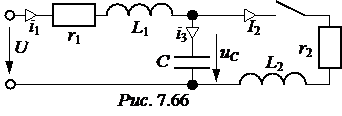
ЗАДАЧА 7.44. Построить график напряжения на конденса-торе uC(t) схемы рис. 7.66, при условии r1 = 60 Ом, L1= 0,2 Гн, r2 = 40 Ом, L2= 0,1 Гн, C = 100 мкФ, u = 100 В. Комментарии и ответы. Задачу 7.44 решим по той же самой методике, что и задачу 7.43. Исходные данные: j:= U:= 100 r1:= 60 r2:= 40 L:= 0.1 C:= 10-4 Переменные состояния: i1, i2, uC. Независимые начальные условия: i1(0+) = i1(0-) = 0, i2(0+) = i2(0-) = 0, uC(0+) = uC(0-) = u = 100 В x0:=
E:= |K - l·E| |K - l·E| = 0 Перезадание корней характеристического уравнения l:= Коэффициенты ai находят из следующей системы уравнений:
a0 + l2 a1 + l22 a2 = el2·t, a0 + l3 a1 + l32 a2 = el3·t. D:= a0(t):= a1(t):= a2(t):=
В случае трёх корней характеристического уравнения матричная экспонента находится в виде eKt = a0 Е + a1[K] + a2[K]2, eK(t):= a0(t)·E + a1(t)·K + a2(t)·K2
Попробуем получить ответ для uC(t):
По данной формуле MathCAD отказывается давать значения напряже-ния в отдельные моменты времени. Поэтому произведём перезадание uC(t):
Значение напряжения, например, в момент времени t = 0,01 с:
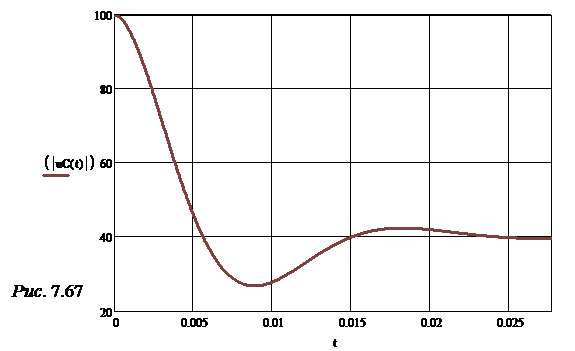
Примечание. Как и в задаче 7.43 значения a0, a1, eKt и, конечно же, uC должны быть в любой момент времени действительными числами. Здесь же значение uC(0,01) оказалось комплексным. Это объясняется тем, что при перезадании корней характеристического уравнения li было сделано округление ответов до четырёх значащих цифр, что внесло в последующие вычисления некоторую погрешность. Например, у значений напряжения на конденсаторе появилась мнимая часть. Однако она мала и ей можно пренебречь. Можно утверждать, что реальное значение напряжения на конденсаторе практически равно модулю от полученного комплексного значения. В связи с этим строим график модуля напряжения uC в функции времени t (рис.7.67).и |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 313. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
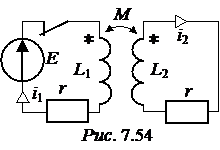 ЗАДАЧА 7.35. В схеме рис. 7.54 с числовыми значениями задачи 7.31 рассчитать ток i2 в случае размыкающегося ключа.
ЗАДАЧА 7.35. В схеме рис. 7.54 с числовыми значениями задачи 7.31 рассчитать ток i2 в случае размыкающегося ключа. = 10 А.
= 10 А.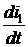 + r×i2 + L2
+ r×i2 + L2 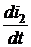 = 0.
= 0.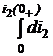 = M
= M 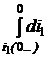 или L2i2(0+) = -Mi1(0–) = -0,05×10 = -0,5 Вб.
или L2i2(0+) = -Mi1(0–) = -0,05×10 = -0,5 Вб.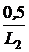 = -
= - 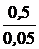 = -10 А.
= -10 А.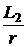 =
= 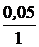 = 0,05 с.
= 0,05 с.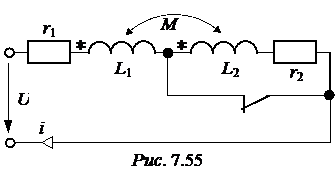
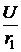 =
= 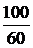 = 1,667 А, во второй катушке тока не было – i2(0-) = 0.
= 1,667 А, во второй катушке тока не было – i2(0-) = 0.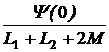 =
= 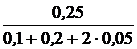 = 0,625 А.
= 0,625 А.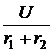 =
= 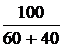 = 1 А.
= 1 А.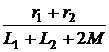 = -
= - 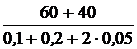 = -250 с -1.
= -250 с -1.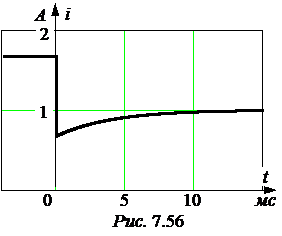 4. Свободная составляющая тока
4. Свободная составляющая тока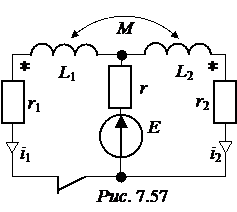 ЗАДАЧА 7.37. Рассчитать ток второй катушки в схеме рис. 7.57 со сле-дующими числовыми данными: Е = 11,7 В, r1 = 1 Ом, r2 = 9 Ом, r = 3 Ом, L1= 10 мГн, L2= 20 мГн, М = 10 мГн.
ЗАДАЧА 7.37. Рассчитать ток второй катушки в схеме рис. 7.57 со сле-дующими числовыми данными: Е = 11,7 В, r1 = 1 Ом, r2 = 9 Ом, r = 3 Ом, L1= 10 мГн, L2= 20 мГн, М = 10 мГн.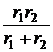 = 3 +
= 3 + 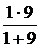 = 3,9 Ом,
= 3,9 Ом,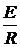 ×
× 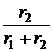 =
=  = 2,7 А,
= 2,7 А,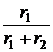 =
= 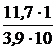 = 0,3 А.
= 0,3 А.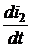 + М
+ М 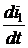 = Е или L2di2=-Mdi1
= Е или L2di2=-Mdi1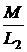 i1(0-) + i2(0-) =
i1(0-) + i2(0-) = 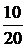 ×2,7 + 0,3 = 1,65 А.
×2,7 + 0,3 = 1,65 А.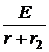 =
= 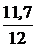 = 0,975 А.
= 0,975 А. = -
= - 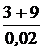 = -600 с -1.
= -600 с -1.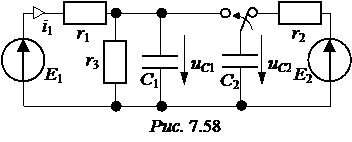
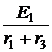 ×r3 =
×r3 =  = 24 B, uС2(0-) = -Е2= -6 В.
= 24 B, uС2(0-) = -Е2= -6 В. 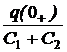 =
= 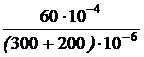 = 12 B.
= 12 B.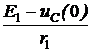 =
= 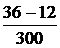 = 0,08 А = 80 мА.
= 0,08 А = 80 мА.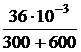 = 40 мА.
= 40 мА. = -
= - 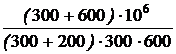 = -10 с –1,
= -10 с –1,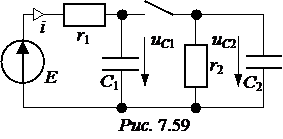 ЗАДАЧА 7.39. В схеме рис. 7.59 найти закон изменения тока источника ЭДС при замыкании контакта. Числовые данные: Е = 60 В, r1 = r2 = 1 кОм,
ЗАДАЧА 7.39. В схеме рис. 7.59 найти закон изменения тока источника ЭДС при замыкании контакта. Числовые данные: Е = 60 В, r1 = r2 = 1 кОм,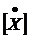 = [K]´[X] + [L]´[F],
= [K]´[X] + [L]´[F],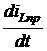 = 0,
= 0, 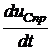 = 0. Уравнения состояния принимают вид: 0 = [K]´[Xnp] + [L]´[F],
= 0. Уравнения состояния принимают вид: 0 = [K]´[Xnp] + [L]´[F],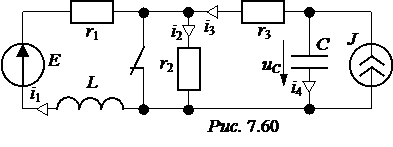 Решение
Решение 2. Независимые начальные условия:
2. Независимые начальные условия: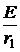 =
= 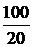 = 5 А,
= 5 А,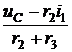 =
= 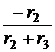 ×i1 +
×i1 + 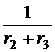 ×uC.
×uC.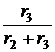 ×i1 +
×i1 + 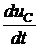 = J – i3 =
= J – i3 = 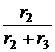 ×i1 –
×i1 – 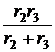 )×i1 –
)×i1 – 
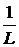 (r1+
(r1+ 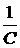 i1 –
i1 – 
 -(r1+
-(r1+ 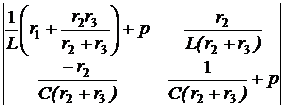 =
=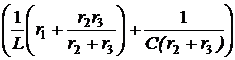 ×р +
×р + 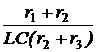 = р2 + 555,6р + 138900 = 0.
= р2 + 555,6р + 138900 = 0.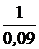 ×27,5×5 – 0,75×
×27,5×5 – 0,75× 
 А×sinY1 = 6, B×sinYu = -120,
А×sinY1 = 6, B×sinYu = -120,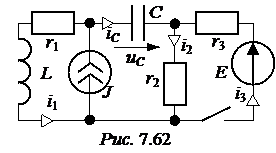 = 11,25×е –277,8t×sin(248,5t + 138,17°) А.
= 11,25×е –277,8t×sin(248,5t + 138,17°) А.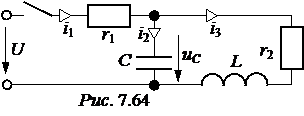
 i1(t) = 0,8×е –16,67t – 0,3×е –100t А;
i1(t) = 0,8×е –16,67t – 0,3×е –100t А;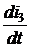 = uL = uC – r2×i3; i1 =
= uL = uC – r2×i3; i1 = 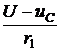 ; С
; С 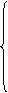
 i3 +
i3 + 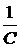 i3 –
i3 – 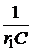 uC +
uC + 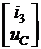 , [K] =
, [K] = 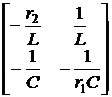 , [L]´[F] =
, [L]´[F] = 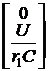 , [X(0)] =
, [X(0)] = 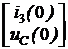 =
= 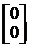 .
.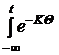 ·L´F(q)·dq, то есть
·L´F(q)·dq, то есть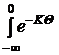 ·L´F(q)·dq + eKt
·L´F(q)·dq + eKt 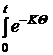 ·L´F(q)·dq =
·L´F(q)·dq =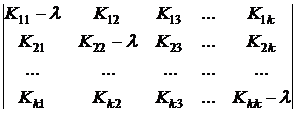 = 0.
= 0.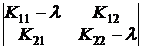 = 0.
= 0. a0 + l1 a1 = el1·t, a0 =
a0 + l1 a1 = el1·t, a0 = 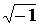 ORIGIN:= 1 U:= 100 r1:= 60 r2:= 40 L:= 0.1 C:= 10-4
ORIGIN:= 1 U:= 100 r1:= 60 r2:= 40 L:= 0.1 C:= 10-4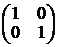 x0:=
x0:=  K:=
K:= 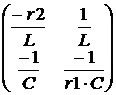 LF(q):=
LF(q):= 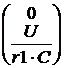
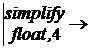 .1667e6 + 566.7·l + l2
.1667e6 + 566.7·l + l2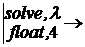
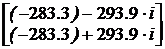
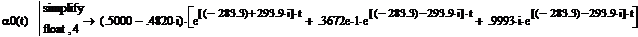
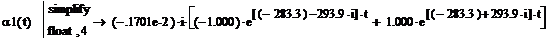
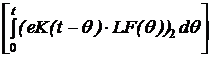 i1(t):=
i1(t):= 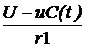
 Примечание. Ответы для коэффициентов a0, a1, искомых токов i1(t) и i3(t) (то же наблюдается и в отношении матричной экспоненты eKt) содержат комплексные числа. Это объясняется комплексностью корней характеристического уравнения. Однако, благодаря тому, что корни являются комплексными сопряжёнными числами, значения указанных величин в любой момент времени оказываются действительными, в связи с чем возможно построение графиков токов. Приведение же ответов для токов к стандартному виду с затухающей синусоидой требует дополнительных действий. В этом состоит недостаток данного метода. Графики искомых токов показаны на рис. 7.65.
Примечание. Ответы для коэффициентов a0, a1, искомых токов i1(t) и i3(t) (то же наблюдается и в отношении матричной экспоненты eKt) содержат комплексные числа. Это объясняется комплексностью корней характеристического уравнения. Однако, благодаря тому, что корни являются комплексными сопряжёнными числами, значения указанных величин в любой момент времени оказываются действительными, в связи с чем возможно построение графиков токов. Приведение же ответов для токов к стандартному виду с затухающей синусоидой требует дополнительных действий. В этом состоит недостаток данного метода. Графики искомых токов показаны на рис. 7.65. 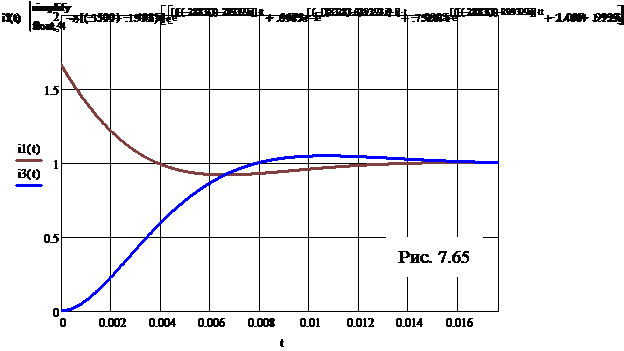

 Система уравнений состояния:
Система уравнений состояния: 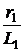 i1 –
i1 – 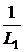 uC +
uC +  i2 +
i2 + 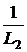 uC ,
uC ,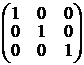 K:=
K:= 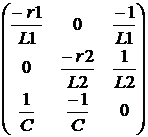 LF(q):=
LF(q):= 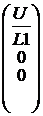
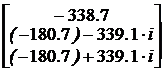
 a0 + l1 a1 + l12 a2 = el1·t,
a0 + l1 a1 + l12 a2 = el1·t,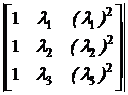
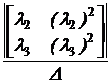 ·
· 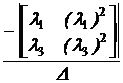 ·
· 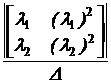 ·
· 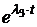
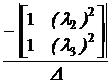 ·
· 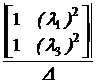 ·
· 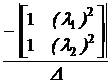 ·
· 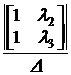 ·
· 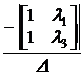 ·
· 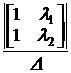 ·
· 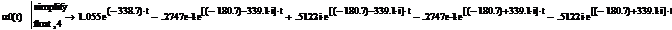 Ответ, например, для коэффициента a0(t):
Ответ, например, для коэффициента a0(t):