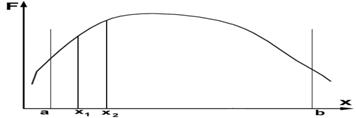
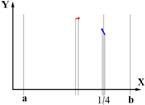
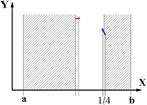
Поиск экстремума унимодальной функции

Пусть известно, что целевая функция имеет только один экстремум на интервале a, b. Такая функция F=f(x) называются унимодальными. Определим значения ЦФ при X=x₁ и x₂. С точки зрения расположения экстремума (в примере – максимума) возможны три варианта:

F(x₁) < F(x₂) – максимум лежит в между x₂ и b.

F(x₁) = F(x₂) – максимум лежит между x₂ и x₁.

F(x₁) > F(x₂) – максимум лежит в между x₁ и a.

Это означает, что при выполнении первого условия на отрезке [x₁, b] не может находиться x_opt, следовательно, его можно исключить из дальнейшего рассмотрения. Если же выполняется третье условие, то на отрезке [a, x₂] не может находиться x_opt, следовательно, его можно исключить из рассмотрения. Выбирая новые x₂ и x₁ и последовательно повторяя анализ, сужаем область определения экстремума до любого разумного предела. Выбор значений x₂ и x₁ с учетом предыдущих результатов определяет различие методов последовательного поиска.

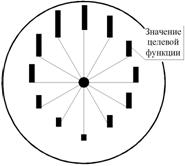
Например, метод половинного деления (дихотомии), когда пары x₂ и x₁ выбираются симметрично относительно центра текущего интервала, на расстоянии ±d от него, где d - некоторая константа. Если при прямом переборе эффективность поиска оптимума прямо пропорционально числу расчетов, то по методу дихотомии она возрастает с ростом итераций экспоненциально. Например, если при прямом переборе требуется 1000 расчетов для того, чтобы сузить зону поиска экстремума в N раз, то по методу дихотомии – только 20.

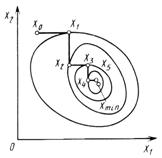
Поиска экстремума методом покоординатного спуска

Направление поиска на каждом шаге совпадает с направлением одной из координатных осей. Например, вначале осуществляется движение в направлении оси X1, до тех пор, пока целевая функция уменьшается. Когда такое уменьшение прекращается, начинается движение в направление X2 и т.д. После окончания спуска по всем осям вновь возвращаются к X1 и цикл повторяется. Так продолжается до тех пор, пока не находя минимум целевой функции с заданной точностью. Траектория спуска для двух переменных показана на рисунке.

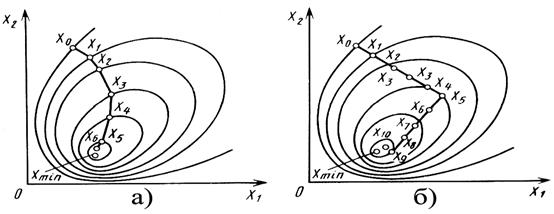
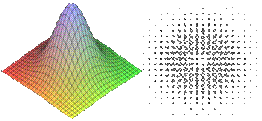
Поиска экстремума методом градиента и методом наискорейшего спуска

В основе этих методов, как и всех градиентных методов, лежит то, что направление уменьшения ЦФ всегда противоположно направлению ее градиента. Градиент – вектор, проекции которого на оси координат равны частным производным по каждой переменной в данной точке.

ß нахождение градиента

Метод градиента (рисунок «а») предусматривает определение этого направления (градиента) в каждой точке траектории спуска. При методе наискорейшего спуска (рисунок «б») движение в направление, противоположном градиенту, осуществляется до тех пор, пока происходит уменьшение целевой функции. При этом в каждой точке вычисляется только значение функции, а градиент вычисляется только для тех точек, где функция перестает уменьшаться. На рисунке изображена траектория спуска по методу градиента (а) и по методу наискорейшего спуска (б). Сравнивая траектории, можно увидеть, что метод наискорейшего спуска требует большего числа шагов, но при этом методе реже вычисляется градиент целевой функции.