
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нахождение числа всех подмножеств данного множестваЕсли задано некоторое множество А, то можно рассматривать новое множество М (А) – множество всех его подмножеств. Пример 1. Сколько подмножеств имеет множество А={é}? По свойствам отношения включения, имеем Æ Таким образом, одноэлементное множество А={é} имеет 2 подмножества. Пример 2. Сколько всего подмножеств имеет двухэлементное множество А={а, в}? По свойствам отношения включения, имеем Æ Одноэлементные подмножества: {а}, {в}. Таким образом, двухэлементное множество А={а, в} всего имеет 4 подмножества. Пример 3. Сколько всего подмножеств имеет трехэлементное множество А = {, ○, ◊}? По свойствам отношения включения, имеем Æ Одноэлементные подмножества: {}, {○}, {◊}. Двухэлементные подмножества: {, ○}, {, ◊}, {○, ◊}. Таким образом, трехэлементное множество А = {, ○, ◊} всего имеет 8 подмножеств. Пример 4. Сколько всего подмножеств имеет четырехэлементное множество А = {а, в, с, d}? По свойствам отношения включения, имеем Æ Одноэлементные подмножества: {а}, {в}, {с}, {d}. Двухэлементные подмножества: {а, в}, {а, с}, {a, d}, {в, с}, {в, d}, {с, d}. Трехэлементные подмножества: {а, в, с}, {a, в, d}, {а, с, d}, {в, с, d}. Таким образом, четырехэлементное множество всего имеет 16 подмножеств. Нетрудно заметить, что с увеличением количества элементов множества А, число всех его подмножеств значительно увеличивается. Возникает вопрос: сколько подмножеств имеет множество из n – элементов? Ответ на поставленный вопрос дает следующее утверждение. Теорема 5.Конечное множество, содержащее n элементов, имеет 2п подмножеств, то есть если Ап = {а1, а2, ... , aп }, то п(М(Ап))=2п.  Доказательствопроведем, используя метод математической индукции. 1) Путь п = 1, то есть А1 = { а1}. Значит, М(А1)= {Æ, { а1}}. В этом случае п(М(А1)) = 21 = 2 что и доказывает справедливость теоремы при п = 1. 2) Пусть п = к, то есть Aк = { а1, а2, ..., aк }. Предположим, что п(М(Aк)) = 2 3) Докажем, что тогда множество Aк+1, имеет 2 Таким образом, п(М(Aк+1)) = 2 На основании метода математической индукции можно сделать вывод, что Теорема. 5 справедлива для любого натурального числа п. Теорема доказана. Понятие факториала Название «факториал» происходит от слова «factor» − «множитель». Термин «factorielle» ввёл французский математик Луи Арбогаст (1759–1803) в 1800 году.[13] Факториал– это функция, определённая на множестве целых неотрицательных чисел По определению 0! = 1, 1! = 1. Обозначение n! впервые использовал французский математик Христиан Крамп (1760 – 1826 гг.) в 1808 году. По определению факториала имеем: Пример 1. Вычислим: Пример 2. Упростим выражение:
Пример 3. Докажем формулу ÿ Воспользуемся методом математической индукции. 1) При п=1 имеем, 2) Предположим, что формула верна, для п=к, то есть 3) Докажем, что формула верна, для п=к+1, то есть
Действительно, = На основании метода математической индукции заключаем, что формула верна для любого натурального числа п. Пример 4. Найти сумму Решение.Заменим каждое слагаемое разностью по формуле
Имеем, = Следовательно,
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 481. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 А и А
А и А  .
.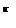 , то есть множество Aк имеет 2
, то есть множество Aк имеет 2 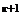 подмножеств. В самом деле, если к элементам множества Aк, содержащего к элементов, добавить еще один элемент aк+1, то к имеющимся 2
подмножеств. В самом деле, если к элементам множества Aк, содержащего к элементов, добавить еще один элемент aк+1, то к имеющимся 2  .
. , значение которой равно произведению целых неотрицательных чисел от 1 до данного числа n, то есть 1∙2∙3∙ …∙n; Обозначают символом n!.
, значение которой равно произведению целых неотрицательных чисел от 1 до данного числа n, то есть 1∙2∙3∙ …∙n; Обозначают символом n!.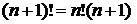 ,
,  .
.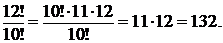


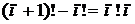 .
. откуда 1=1, значит для п=1 формула верна.
откуда 1=1, значит для п=1 формула верна. .
. .
.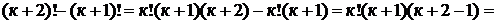
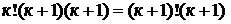 , что и требовалось доказать.
, что и требовалось доказать.
 .
.
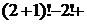

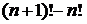

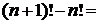
 так как все слагаемые в левой части равенства, за исключением второго и предпоследнего взаимно уничтожаются.
так как все слагаемые в левой части равенства, за исключением второго и предпоследнего взаимно уничтожаются. =
= 