
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Неопределенные степенно-показательные выраженияРассмотрим теперь степенно-показательное выражение Если для Доказательство опускаем. Очевидно, что исключительные случаи отвечают таким комбинациям значений a и b: a = 1, b = ∞; a = 0, b = 0; a = +∞, b = 0. В этих случаях говорят, что выражение В качестве примера неопределенности вида 1¥ приведем выражение
имеет исключительную важность, как для самого анализа, так и для его приложений. Вот первые семь знаков его разложения в десятичную дробь: е = 2,718281… Некоторые свойства числа е делают особенно выгодным выбор этого числа в качестве основания для системы логарифмов. Логарифмы по основанию е называются натуральными и обозначаются знаком ln без указания основания. Десятичные логарифмы связаны с натуральными формулой:
Таким образом, поставив себе задачей – определить пределы последовательностей, заданных арифметическими (1.10) или степенно-показательным выражениями, по пределам последовательностей 
Монотонные последовательности Если члены последовательности суть значений монотонной числовой функции переменного п, то последовательность называется монотонной или, по типу монотонной функции соответственно: возрастающей, неубывающей, убывающей, невозрастающей последовательностями. Для монотонной последовательности справедлива следующая теорема, условие которой является достаточным условием для сходимости (существования конечного предела) последовательности. Теорема. Ограниченная монотонная последовательность всегда имеет конечный предел, т.е. является сходящейся. Эту теорему примем без доказательства. Если последовательность не является монотонной, то условие данной теоремы, как следует из теоремы 2 (п.5.2), является, лишь необходимым, но не достаточным. Пример. Доказать, что последовательность Доказательство. Покажем, что эта последовательность ограничена. Представим ее общий член в виде
Исследуем эту же последовательность на монотонность. Найдем разность
Таким образом,
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 381. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
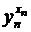 и последовательность
и последовательность 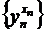 при условии, что
при условии, что 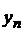 > 0 " nÎN.
> 0 " nÎN.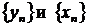 существуют конечные пределы:
существуют конечные пределы:  и
и 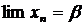 , причем a >0, то
, причем a >0, то 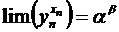 .
.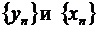 , а нужно непосредственно учесть закон, по которому они стремятся к своим пределам.
, а нужно непосредственно учесть закон, по которому они стремятся к своим пределам.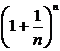 . Последовательность
. Последовательность 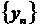 , определенная этим выражением,
, определенная этим выражением, 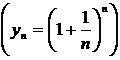 имеет конечный предел. По примеру Эйлера, его всегда обозначают буквой е. Это иррациональное число
имеет конечный предел. По примеру Эйлера, его всегда обозначают буквой е. Это иррациональное число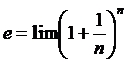 (1.11)
(1.11) .
.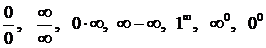 . В этих случаях приходится, учитывая закон изменения последовательностей
. В этих случаях приходится, учитывая закон изменения последовательностей 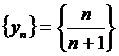 имеет конечный предел, т.е. сходится.
имеет конечный предел, т.е. сходится.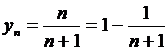 , откуда
, откуда  или
или 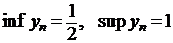 .
.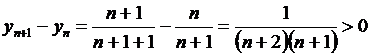 .
.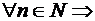 yn+1 > yn, т.е. последовательность монотонно возрастающая. Тогда, по теореме, она имеет конечный предел или сходится. Как было уже доказано (пример гл.1, §5, п.5.1),
yn+1 > yn, т.е. последовательность монотонно возрастающая. Тогда, по теореме, она имеет конечный предел или сходится. Как было уже доказано (пример гл.1, §5, п.5.1), 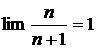 .
.