Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Переведення оцінки в балах в оцінку за 12-бальною системою оцінювання навчальних досягнень учнівСтр 1 из 3Следующая ⇒ ЗБІРНИК ЗАВДАНЬ
для державної підсумкової атестації з математики
Рекомендовано
Міністерством освіти і науки, молоді та спорту України
11
клас
Київ Центр навчально-методичної літератури 2013 ПОЯСНЮВАЛЬНА ЗАПИСКА
Посібник «Збірник завдань для державної підсумкової атестації з математики. 11 клас» призначено для проведення державної підсумкової атестації з математики в одинадцятих класах загальноосвітніх навчальних закладів, а також пере-вірки знань і вмінь учнів протягом навчального року. Він містить 50 варіантів атестаційної роботи, кожний з яких складається із чотирьох частин. Ці частини відрізняються за формою тестових завдань і за рівнем їх складності. Зміст усіх завдань відповідає чинним навчальним програмам з матема-тики: для рівня стандарту, академічного рівня, профільного рівня та рівня поглибленого вивчення математики.
Учні загальноосвітніх класів, які вивчали математику за програмою рівня стандарту, виконують усі завдання першої та другої частин, а також два завдання з третьої частини — завдання достатнього рівня з алгебри і почат-ків аналізу та одне із завдань високого рівня за власним вибором. Якщо учень розв’язав обидва завдання високогорівня, до підсумкового результату зараховується лише один (кращий) результат.
Учні, які вивчали математику за програмою академіч-ного рівня, виконують усі завдання першої, другої та тре-тьої частин атестаційної роботи.
Учні загальноосвітніх класів, які вивчали математику за програмою профільного рівня, виконують усі завдання першої, другої та третьої частин атестаційної роботи, а також два завдання із четвертої частини — одне з двох завдань з алгебри і початків аналізу за власним вибором та одне з двох завдань з геометрії за власним вибором. 
Якщо учень розв’язав обидва завдання з алгебри і початків аналізу, до підсумкового результату зараховується лише один (кращий) результат. Те саме стосується і завдань з геометрії. Учні класів (шкіл) з поглибленим вивченням матема-тики, які продовжували вивчення двох предметів «Алге-бра і початки аналізу» та «Геометрія» за програмою по-глибленого рівня, виконують усі завдання першої, другої, третьої та четвертої частин атестаційної роботи.
Державна підсумкова атестація з математики проводиться протягом 3 академічних годин для учнів, які вивчали мате-матику за програмою рівня стандарту та академічного рівня. Учні класів, що вивчали математику за програмою профіль-ного рівня, виконують атестаційну роботу протягом 3,5 ака-демічної години, а учні класів (шкіл) з поглибленим вивчен-ням математики — 4 академічних годин.
3
У першій частині атестаційної роботи пропонується 12 зав дань з вибором однієї правильної відповіді. До кожного завдання наведено чотири можливі варіанти відповіді, з яких тільки одна є правильною. Завдання з вибором однієї відповіді вважається виконаним правильно, якщо в бланку відповідей1 указано тільки одну літеру — ту, якою позначено правильну відповідь. Будь-яких міркувань, що пояснюють вибір відповіді, учень наводити не повинен.
Розподіл завдань першої частини за класами, предметами та рівнями навчальних досягнень учнів наведено в таблиці 1.
Кожне правильно розв’язане завдання 1.1–1.12 першої частини оцінюється одним балом. Якщо в бланку відповідей указано правильну відповідь, то за виконання цього завдання
1 Зразок бланка відповідей наведено в кінці збірника.
4
нараховується 1 бал, якщо ж указана учнем відповідь є не-правильною, то виконання завдання оцінюється в 0 балів. Друга частина атестаційної роботи складається із4за- вдань відкритої форми з короткою відповіддю. Завдання цієї частини вважається виконаним правильно, якщо в бланку відповідей записано тільки правильну відповідь (наприклад, число, вираз, корені рівняння тощо). Усі необхідні обчислен-ня, перетворення тощо учні виконують на чернетках.
Розподіл завдань другої частини за класами, предметами та рівнями навчальних досягнень учнів наведено в таблиці 2.
Правильне розв’язання кожного із завдань 2.1–2.4 оціню-ється двома балами: якщо в бланку відповідей указано пра-вильну відповідь до завдання, то за це нараховується 2 бали, якщо ж указана учнем відповідь є неправильною, то бали за таке завдання не нараховуються. Часткове виконання за-вдання другої частини (наприклад, якщо учень правильно знайшов один з двох коренів рівняння або розв’язків системи рівнянь) оцінюється 1 балом.
Якщо учень вважає за потрібне внести зміни в уже за-писану в бланк відповідь до якогось із завдань першої чи другої частини, то він має це зробити тільки в спеціаль-но відведеній для цього частині бланка. Таке виправлення не веде до втрати балів. Якщо ж виправлення зроблено в основній частині бланка відповідей, то бали за таке за-вдання не нараховуються. Третя та четверта частини атестаційної роботи скла- даються із завдань відкритої форми з розгорнутою відповід- дю.Такі завдання вважаються виконаними правильно,якщо
5
Третя частина атестаційної роботи містить три завдання, четверта частина — чотири. Розподіл завдань третьої та чет-вертої частин за класами, предметами та рівнями навчальних досягнень учнів наведено в таблицях 3 і 4.
Правильне розв’язання завдання 3.1 оцінюється чотирма балами, а кожне із завдань 3.2, 3.3, 4.1м–4.4м — шістьма ба лами.
Оцінювання в балах виконання завдань третьої та четвер-тої частин атестаційної роботи здійснюється за критеріями, наведеними в таблиці 5.
6
Таблиця 5
Примітка.У випадку,коли учні загальноосвітніх класів,яківивчали математику за програмою профільного рівня, а також учні класів з поглибленим вивченням математики правильно розв’язали стереометричні задачі 3.3 і 4.4м і навели повне об-ґрунтування розв’язання однієї з них, а до другої задачі пра-вильно записали хід розв’язування із частковим обґрунтуван-ням його кроків, то обидві задачі оцінюються у 6 балів.
Виправлення і закреслення в оформленні розв’язання за-вдань третьої та четвертої частин, якщо вони зроблені аку-ратно, не є підставою для зниження оцінки. Наведені критерії мають бути відомі учням.
Переведення оцінки в балах в оцінку за 12-бальною системою оцінювання навчальних досягнень учнів Сума балів, нарахованих за виконані учнем завдання, пе-реводиться в оцінку за 12-бальною системою оцінювання на-вчальних досягнень учнів за спеціальною шкалою.
7
Для учнів класів, які вивчали математику на рівні стан-дарту, максимально можлива сума балів за атестаційну робо-ту становить 30 (див. табл. 6). Відповідність кількості набра-них учнем балів оцінці за 12-бальною системою оцінювання навчальних досягнень учнів наведено в таблиці 7.
Таблиця 6
Таблиця 8
8
Для учнів, які вивчали математику на профільному рівні, максимально можлива сума балів за атестаційну роботу ста-новить 48 (див. табл. 10). Відповідність кількості набраних учнем балів оцінці за 12-бальною системою оцінювання на-вчальних досягнень учнів наведено в таблиці 11.
Таблиця 10
Для учнів класів з поглибленим вивченням математики максимально можлива сума балів за атестаційну роботу ста-новить 60 (див. табл. 12). Відповідність кількості набраних учнем балів оцінці за 12-бальною системою оцінювання на-вчальних досягнень учнів наведено в таблиці 13.
Таблиця 12
9
Зразок виконання завдань атестаційної роботи і заповнен ня бланка відповідей для першої та другої частин розглянемо на прикладі одного з варіантів.
Частина перша
Завдання 1.1–1.12 мають по чотири варіанти відповіді, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначте її у бланку відповідей.
Розв’язання. D = 22 – 4 · 1 · (–3) = 4 + 12 = 16. Відповідь.Б).
1.4.Відомо,щоa>bіb> 0.Яка з нерівностей правильна?
А)a<0; Б)–a>–b; В)
Відповідь. Г).
1.5.Яка з функцій показникова?
А)y=x2; Б)y=2x; В)y=(–2)x;Г)y=0x. Відповідь. Б).
1.6.На якому з рисунків зображено графік функціїy=sin(π–x)?
А)
10
Б)
В)
Г)
Розв’язання. Оскільки sin(π – x) = sinx для будь-якого значення x, то маємо функцію y = sinx. Її графік зобра-жено на рисунку А).
Відповідь. А).
1.7.Яка з функцій є первісною для функціїf(x)=2x?
Розв’язання. Оскільки ( x2 + 7)′ = 2x, то F(x) = x2 + 7 є первісною для функції f(x) = 2x.
Відповідь. В).
1.8.Знайдітьпроміжок зростання функціїf(x)=x2– 4x+ 3. А)(– ; –2]; Б)[–2; + ); В)[2; + ); Г)(– ; 2].
Розв’язання. f′(x) = 2x – 4; f′(x) = 0, коли x = 2. Функція зростає на про- міжку [2; + ).
Відповідь. В).
1.9.Сума трьох сторін ромба дорівнює 12 см. Знайдіть його периметр.
А)12 см; Б)16 см; В)24 см; Г)48 см.
Розв’язання. Сторона ромба а = 12 : 3 = 4 (см), його периметр Р = 4а = 4 · 4 = 16 (см).
Відповідь. Б).
11
АВ = = 15 : =
Відповідь.Г).
1.11.Радіус основи конуса дорівнює 4 см, а твірна – 5 см. Знайдіть площу бічної поверхні конуса.
А)20 см2; Б)20π см2; В)12π см2; Г)15π см2.
Розв’язання.
r =4 см; l =5 см; Sбіч= π ∙ r ∙ l = π· 4 · 5=20π(см2).
Відповідь. Б).
1.12.Порівняйте довжини відрізків АС і ВС, якщо А(–2; 3; 4), В(0; 4; –1), С(5; 4; 4).
А)АС>ВС; В)АС=ВС;
Б)АС<ВС; Г)порівняти неможливо.
Розв’язання.
Отже, АС = ВС.
Відповідь. В).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 468. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||







 Ïoÿñíþâàëüíà çàïèñêà
Ïoÿñíþâàëüíà çàïèñêà
 Ïoÿñíþâàëüíà çàïèñêà
Ïoÿñíþâàëüíà çàïèñêà


 Ïoÿñíþâàëüíà çàïèñêà
Ïoÿñíþâàëüíà çàïèñêà



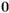 ; Г) –2a < –2b.
; Г) –2a < –2b.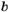

 Çðàçîê
Çðàçîê А)F(x)=2;Б)F(x)=2 +x;В)F(x)=x2+ 7;Г)F(x)=2x.
А)F(x)=2;Б)F(x)=2 +x;В)F(x)=x2+ 7;Г)F(x)=2x.

 = 25 (см).
= 25 (см).