
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Примерные решения некоторых тематических задачЭлементы линейной алгебры. Задача 1. Решить систему линейных уравнений:
а) методом Гаусса; б) с помощью определителей; Решение а) Исключим из последних двух уравнений х1. Для этого умножим первое уравнение на (–5) и результаты прибавим соответственно ко второму уравнению, затем обе части первого уравнения умножим на (–3) и результаты прибавим к третьему уравнению. В результате получим систему, эквивалентную данной:
Разделив обе части второго уравнения системы (1) на 2, получим систему
Теперь исключим из третьего уравнения системы (2) переменную х2. Для этого обе части второго уравнения этой системы умножим на (-7) и результаты прибавим к третьему уравнению. В результате получим систему
Откуда x3 = 3, х2 = 1 и х1 = –2. Приведение данной системы к ступенчатому виду (3) практически более удобно, если использовать преобразования расширенной матрицы данной системы, то есть матрицы, составленной из коэффициентов при неизвестных и свободных членов. Для удобства столбец свободных членов этой матрицы отделим вертикальной чертой. Расширенная матрица данной системы имеет вид:
Умножим элементы первой строки матрицы на (–5) и результаты прибавим к элементам второй строки, затем умножим элементы первой строки на (–3) и результаты прибавим к элементам третьей строки. Получим матрицу
Разделив элементы второй строки на 2, получим
Элементы второй строки умножим на (–7) и результаты прибавим к элементам третьей строки. Получим матрицу, 
которая позволяет данную систему привести к виду (3) и затем решить ее.
б) Составим и вычислим следующие определители системы. Определитель
Аналогично вычисляем Тогда решения системы найдём по формулам: Дифференциальное исчисление
Задача 2.Найти производные а) г)
Решение:
При нахождении производных функций используем правила дифференцирования и таблицу основных элементарных функций. Правила дифференцирования:
1.
2.
3.
4. 5. 6. 7.
Таблица производных основных элементарных функций:
а) Пользуясь правилом логарифмирования, корня и дроби, преобразуем правую часть:
Применяя правила и формулы дифференцирования, получим:
б) Предварительно прологарифмируем по основанию е обе части равенства:
Теперь дифференцируем обе части, считая
откуда
в) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную у', следует дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, азатем полученное уравнение решить относительно искомой производной у'. Имеем
Из полученного равенства, связывающего х, у и
откуда
г) воспользуемся правилом дифференцирования частного, получаем:
д) Воспользуемся правилом дифференцирования сложной функции.
Неопределенный интеграл
Задача 3.Найти неопределённые интегралы: а) Решение:
При нахождении неопределённых интегралов функций используют следующие свойства: 1) 2) и таблицу интегралов основных элементарных функций:
1. 2. 3. 4. 5. 6. 7. 9'. 8. 10'. 9. 11'. 10. 11. 12. 13. 14. а) Подынтегральное выражение представляет собой неправильную рациональную дробь, так как степень многочлена, стоящего в числителе, больше степени многочлена, стоящего в знаменателе. Поэтому выделим целую часть дроби (разделим числитель на знаменатель с остатком).
Тогда данную дробь можно записать в виде
Правильная рациональная дробь может быть представлена в виде суммы простейших дробей четырёх типов: 1) Выпишем знаменатель дроби и разложим его на множители
Знаменатель представляет собой произведение линейных множителей в первой степени, следовательно, дробь можно разложить на сумму простейших дробей первого типа.
Приравниваем коэффициенты при одинаковых степенях многочленов, стоящих в числителях дробей
Решая систему, получим Значит, подынтегральная дробь представится в виде
Следовательно,
б) Подынтегральное выражение представляет собой правильную рациональную дробь. Разложим знаменатель на множители:
Выпишем подынтегральную дробь и разложим её на сумму простейших дробей первого и второго типа, т. к. знаменатель дроби представляет собой произведение линейных множителей, один из которых кратный.
= Приравняем коэффициенты многочленов, стоящих в числителе.
Решая данную систему, получим:
Таким образом, данный интеграл можно записать в виде:
в) Подынтегральное выражение представляет собой правильную рациональную дробь. Выпишем подынтегральную дробь и разложим её на сумму простейших дробей первого и третьего типа, так как знаменатель представляет собой произведение линейного множителя в первой степени и квадратного трёхчлена
Решая данную систему, получим:
г) Подынтегральное выражение представляет собой правильную рациональную дробь. Выпишем подынтегральную дробь и разложим её на сумму простейших дробей третьего и четвёртого типа, т. к. знаменатель представляет собой квадратный трёхчлен
Решая данную систему, получим:
Отдельно найдём последний интеграл. Положим
Окончательно получим
д) Сделаем замену
е) Интегрируем по частям по формуле:
ж) Сделаем замену
з) Сделаем замену
Последний интеграл есть интеграл от рациональной дроби. Выпишем эту дробь и разложим её на сумму простейших.
Решая систему, получим Тогда Следовательно,
и)
к)
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 209. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 (1)
(1) (2)
(2) (3)
(3) .
.


 , составленный из коэффициентов при неизвестных:
, составленный из коэффициентов при неизвестных:
 , полученный из
, полученный из  ,
,  и
и  .
. ,
,  ,
,  .
. следующих функций:
следующих функций: б)
б)  в)
в) 
 ; д);
; д);  .
. ;
; ;
; ;
; ;
; ;
; ;
; .
.





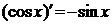





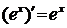




















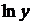 сложной функцией от переменной х:
сложной функцией от переменной х:
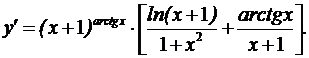

 находим производную у':
находим производную у':








 .
.



 .
. б)
б)  ; в)
; в)  г)
г)  ; д)
; д)  е)
е) 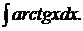 ; ж)
; ж)  ; з)
; з)  и)
и)  ; к)
; к) 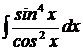 ; л)
; л)  .
.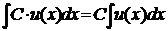 ,
,
 ;
;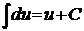 ;
; 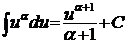 ;
;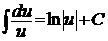 ;
;  ;
; ;
; ;
; ;
; ;
;
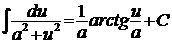 ;
;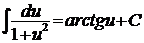 ;
;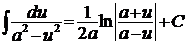 ;
; ;
; ;
; ;
; ;
; ;
;


 ; 2)
; 2) 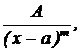 где m – целое число, большее единицы; 3)
где m – целое число, большее единицы; 3)  где
где  то есть квадратный трёхчлен
то есть квадратный трёхчлен  не имеет действительных корней; 4)
не имеет действительных корней; 4)  где n > 1, n – целое число и квадратный трёхчлен
где n > 1, n – целое число и квадратный трёхчлен 








 =
=  =
= .
.
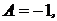
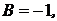
 Имеем:
Имеем: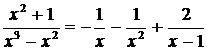 .
.
 , не имеющего действительных корней, также в первой степени.
, не имеющего действительных корней, также в первой степени.
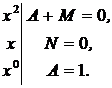


 Имеем
Имеем



 , не имеющего действительных корней, во второй степени.
, не имеющего действительных корней, во второй степени.




 Имеем
Имеем 
 Тогда
Тогда

 тогда
тогда 
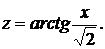 Получим
Получим




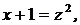
 ,
,
 =
= 
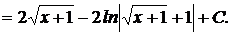
 .
.
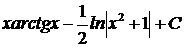 .
. Получим
Получим

 Получим
Получим 

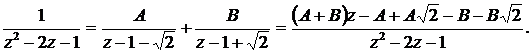








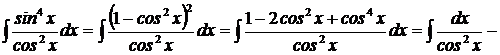

 л)
л) 
