Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕЗадача 55.Из генеральной совокупности извлечена выборка объема n, заданная вариантами хi и соответствующими им частотами. Найти несмещенную оценку генеральной средней.
Решение. Множество всех объектов, подлежащих изучению, называется генеральной совокупностью. Множество случайно отобранных объектов называется выборочной совокупностью или выборкой. Для оценки неизвестных параметров теоретического распределения служат статистические оценки. Статистическая оценка, определяемая одним числом, называется точечной оценкой. Точечная статистическая оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, называется несмещенной оценкой. Статистическая оценка, математическое ожидание которой не равно оцениваемому параметру является смещенной. Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя
где хi – варианта выборки (элемент выборки); ni – частота варианты хi (число наблюдений варианты хi); Объем данной выборки равен Далее по формуле (1) вычисляем несмещенную оценку генеральной средней:
Задача 56.По выборке объема n=41 найдена смещенная оценка генеральной дисперсии Решение. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
Несмещенной оценкой генеральной дисперсии является «исправленная дисперсия»
Таким образом, мы получаем искомую несмещенную оценку дисперсии генеральной совокупности: 
Задача 57.Найти доверительный интервал для оценки с надежностью p=0,95 неизвестного математического ожидания a нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение s=5, выборочная средняя Решение. Интервальной оценкой называется интервал, покрывающий оцениваемый параметр. Доверительным интервалом является интервал, который с данной надежностью покрывает оцениваемый параметр. Для оценки математического ожидания a нормально распределенного количественного признака Х по выборочной средней
где В данной задаче t находим из условия Далее получаем
или Задача 58.По данным n=9 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений Решение. Оценкой математического ожидания a нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения является доверительный интервал
По таблице 3 приложения, по заданным n и Таким образом
Окончательно получаем
Задача 59.Из генеральной совокупности извлечена выборка объема n. Оценить с надежностью
Решение. Объем данной выборки равен По данным задачи находим выборочную среднюю:
Далее находим исправленное среднее квадратическое отклонение s:
Для оценки математического ожидания a нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения служит доверительный интервал
По таблице 3 приложения по заданным n и Таким образом
Окончательно получаем
Задача 60.Построить полигон частот и эмпирическую функцию по данному распределению выборки:
Решение. Полигоном частот называют ломаную, отрезки которой соединяют точки Полигон частот для данного распределения изображен на рисунке 15.
Рис. 15
Эмпирической функцией распределения (функцией распределения выборки) называют функцию
где Из определения следует, что Найдем эмпирическую функцию распределения. Объем данной выборки равен Если Аналогично получаем, что при Таким образом, эмпирическая функция распределения равна:
График полученной эмпирической функции распределения изображен на рисунке 16.
Рис. 16
Задача 61.Найти методом сумм асимметрию и эксцесс по заданному распределению выборки объема n=100:
Решение. Асимметрия
где Эксцесс
где Асимметрия и эксцесс служат для оценки отклонения эмпирического распределения от нормального. Для нормального распределения эти характеристики равны нулю. Поэтому, если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального. Кроме того, если эксцесс положительный, то распределение будет островершинным; если отрицательный, то распределение будет плосковершинным по сравнению с нормальным распределением. Для практического расчета асимметрии и эксцесса непосредственно пользоваться вышеуказанными формулами довольно затруднительно, поэтому воспользуемся методом сумм. Составим расчетную таблицу 1, для этого: 1) Запишем варианты в первый столбец. 2) Запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца. 3) В качестве ложного нуля С выберем варианту (68), которая имеет наибольшую частоту (в качестве С можно взять любую варианту, расположенную примерно в середине столбца); в клетках строки, содержащей ложный нуль, запишем нули; в четвертом столбце над и под уже помещенным нулем запишем еще по одному нулю. 4) В оставшихся незаполненными над нулем клетках третьего столбца (исключая самую верхнюю) запишем последовательно накопленные частоты: 2; 2+4=6; 6+6=12; 12+8=20; 20+12=32. Сложив все накопленные частоты, получим число b1=72, которое поместим в верхнюю клетку третьего столбца. В оставшихся незаполненными под нулем клетках третьего столбца (исключая самую нижнюю) запишем последовательно накопленные частоты: 5; 5+7=12; 12+8=20; 20+18=38. Сложив все накопленные частоты, получим число a1=75, которое поместим в нижнюю клетку третьего столбца. 5) Аналогично заполняется четвертый столбец, причем суммируют частоты третьего столбца. Сложив все накопленные частоты, расположенные над нулем, получим число b2=70, которое поместим в верхнюю клетку четвертого столбца. Сумма накопленных частот, расположенных под нулем, равна числу a2=59, которое поместим в нижнюю клетку четвертого столбца. 6) Для заполнения столбца 5 запишем нуль в клетке строки, содержащей ложный нуль (68); над этим нулем и под ним поставим еще по два нуля. В клетках над нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 сверху вниз; в итоге будем иметь следующие накопленные частоты: 2; 2+8=10; 10+20=30. Сложив накопленные частоты, получим число b3=42, которое поместим в верхнюю клетку пятого столбца. В клетках под нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 снизу вниз; в итоге будем иметь следующие накопленные частоты: 5; 5+17=22. Сложив накопленные частоты, получим число a3=27, которое поместим в нижнюю клетку пятого столбца. 7) Аналогично заполняется столбец 6, причем суммируют частоты столбца 5.
В итоге получим расчетную таблицу 1:
Расчетная таблица 1
Теперь найдем di (i=1, 2, 3) и si (i=1, 2, 3, 4):
Найдем условные моменты первого, второго, третьего и четвертого порядков:
Найдем далее центральные эмпирические моменты третьего и четвертого порядков, учитывая, что шаг
Так как дисперсия Учитывая определения асимметрии и эксцесса, окончательно получаем:
ПРИЛОЖЕНИЕ
Таблица 1 Значение функции
Таблица 2 Значение функции
Продолжение табл. 2
Таблица 3 Таблица значений
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА Основная: 1. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного: Учебник для вузов. – М.: Наука, 1989. – 464 с. 2. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 2003. 3. Пискунов Н.С. Дифференциальное и интегральное исчисление. – М.: Наука, 1985 тт.1, 2. 4. Сборник задач по математике для втузов. Под редакцией Ефимова А.В., Демидовича Б.П. – М.: Наука, 1986. тт 1, 2, 3. 5. Хаггарти Р. Дискретная математика для программистов. – М.: Техносфера, 2003. – 320с. – (сер. Мир программирования). 6. Шипачев В.С. Высшая математика. – М.: Высшая школа, 2002. Дополнительная: 1. Беклемишев Л.А. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1984. 2. Бахвалов Н.С. Численные методы. – М.: Лаборатория базовых знаний, 2001 3. Беклемишев Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре. – М.: Наука, 1987. 4. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1975. 5. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. – М.: Наука, 1975 6. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1966. 7. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения. - М.: Наука, 1988. 8. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 2003 9. Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1970. 10. Кудрявцев А.В. Курс математического анализа. – М.: Наука, 1990, тт. 1, 2. 11. Лебедев В.И. Функциональный анализ и вычислительная математика. – М.: Физматлит, 2001. 12. Методы прикладной математики в пожарно-технических задачах. Под ред. Брушлинского Н.Н. М.: ВИПТШ, 1983. 13. Морозова В.Д. Теория функций комплексного переменного. Учебник для вузов. М.: Изд-во МГТУ им. Баумана, 2000 14. Тихонов А.Н., Самарский А.А. Уравнения математической физики. - М.: Наука, 1991. 15. Треногин В.А. Задачи и упражнения по функциональному анализу: Учеб. пос. /В.А.Треногин, Б.М.Писаревский, Т.С.Соболева. – 2-е изд., исп. и доп. – М.: ФИЗМАТЛИТ, 2002. – 240с. 16. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. – М.: Наука, 1975, тт. 1, 2, 3. 17. Шипачев В.С. Задачник по высшей математике. – М.: Высшая школа, 2003. 18. Яблонский С.В. Введение в дискретную математику. - М.: Наука, 1979.
Под редакцией В.С. Артамонова доктора военных наук, доктора технических наук, профессора, заслуженного работника высшей школы Российской Федерации Составители: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 246. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
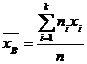 (1),
(1),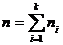 – объем выборки (число элементов совокупности).
– объем выборки (число элементов совокупности).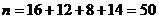 .
.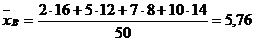
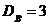 . Найти несмещенную оценку дисперсии генеральной совокупности.
. Найти несмещенную оценку дисперсии генеральной совокупности.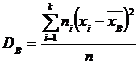
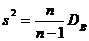 или
или 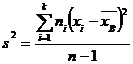
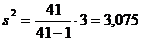
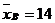 , а объем выборки n=25.
, а объем выборки n=25.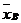 при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал
при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал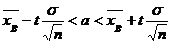 ,
,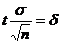 – точность оценки, t – значение аргумента функции Лапласа
– точность оценки, t – значение аргумента функции Лапласа 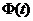 (приложение, таблица 2).
(приложение, таблица 2).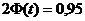 . По таблице 2 определяем
. По таблице 2 определяем 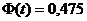 . Таким образом, t=1,96.
. Таким образом, t=1,96.
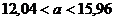
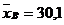 и исправленное среднее квадратическое отклонение s=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью
и исправленное среднее квадратическое отклонение s=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью 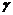 =0,99.
=0,99.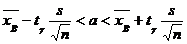 .
.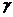 находим
находим 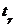 =3,36.
=3,36.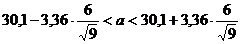
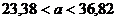
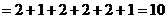
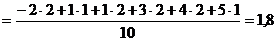
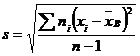
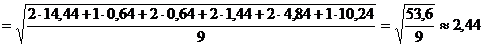
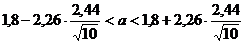
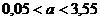
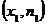 ;
; 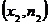 ;…;
;…; 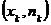 , где хi – варианты выборки, ni – соответствующие им частоты.
, где хi – варианты выборки, ni – соответствующие им частоты.
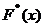 , определяющую для каждого значения x относительную частоту события
, определяющую для каждого значения x относительную частоту события 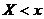 :
: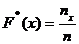 ,
,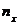 – число вариант, меньших х; n – объем выборки.
– число вариант, меньших х; n – объем выборки.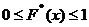 .
.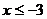 , то
, то 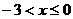 , то значение
, то значение 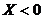 , а именно
, а именно 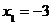 наблюдалось 3 раза, следовательно,
наблюдалось 3 раза, следовательно, 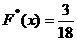 . При
. При 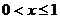 значения
значения  , а именно
, а именно  наблюдались 3+6=9 раз, следовательно,
наблюдались 3+6=9 раз, следовательно, 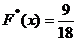 .
.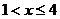 функция распределения
функция распределения 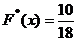 ; при
; при 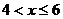 функция распределения
функция распределения 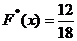 ; при
; при 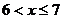 функция распределения
функция распределения 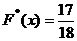 . Далее, если
. Далее, если 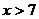 , то
, то 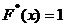 (так как 7 – наибольшая варианта).
(так как 7 – наибольшая варианта).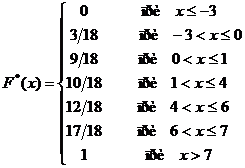
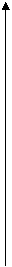








 эмпирического распределения определяется равенством:
эмпирического распределения определяется равенством: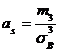 ,
, 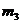 - центральный эмпирический момент третьего порядка, вычисляемый по формуле:
- центральный эмпирический момент третьего порядка, вычисляемый по формуле: 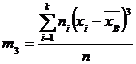
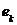 эмпирического распределения определяется равенством:
эмпирического распределения определяется равенством: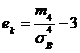 ,
,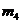 - центральный эмпирический момент четвертого порядка, вычисляемый по формуле:
- центральный эмпирический момент четвертого порядка, вычисляемый по формуле: 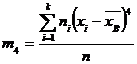
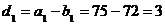 ;
; 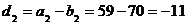 ;
; 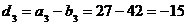 ;
;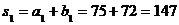 ;
; 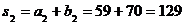 ;
;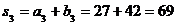 ;
; 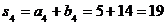 .
.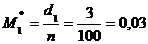 ;
; 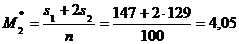 ;
;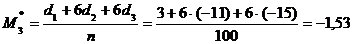 ;
;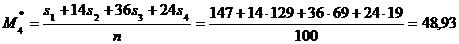 .
.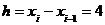 (разность между двумя соседними вариантами):
(разность между двумя соседними вариантами):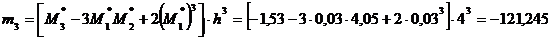 ;
;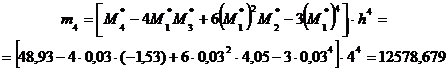
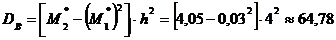 , то выборочное среднее квадратическое отклонение
, то выборочное среднее квадратическое отклонение 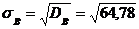 .
.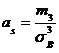
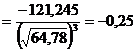 ;
; 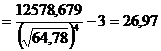 .
.