
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение и анализ дискретных моделейСтр 1 из 4Следующая ⇒ Использование программных систем MATLAB и MAPLE Для автоматизации анализа и проектирования систем управления
Система MATLAB – одна из старейших и тщательно проработанных систем автоматизации математических расчетов. Она была разработана С.В.Молером и с конца 70-х годов широко использовалась на больших ЭВМ. Начиная с версии 4.0, система MATLAB работает в среде Windows. В настоящее время система MATLAB превратилась в одну из самых популярных систем автоматизации математических расчетов и является одним из наиболее часто используемых средств для обучения студентов в университетах всего мира. Области применения системы: стандартные численные расчеты, теория управления, электротехника, обработка сигналов и изображений и т.д. Достоинствами MATLAB являются: · высокое качество численных алгоритмов; · наличие большого числа встроенных средств как для стандартных математических расчетов (линейная алгебра, дифференциальные уравнения, статистика, решение алгебраических и трансцендентных уравнений), так и для специализированных; · хорошее качество двухмерной и трехмерной графики. В состав системы MATLAB входит пакет прикладных программ Control System Toolbox, предназначенный для анализа и синтеза непрерывных и дискретных линейных систем с постоянными коэффициентами. Этот пакет создает удобную вычислительную среду для поддержки автоматизированных расчетов при проектировании систем автоматического управления. Система MAPLE V принадлежит классу программ компьютерной алгебры, работающих с символьным представлением информации. Хотя системасодержит достаточно обширные средства для выполнения численных расчетов, основное назначение системы – выполнение символьных преобразованийвыражений, интегрирование и дифференцирование выражений в символьном виде. Достоинствами системы являются разнообразные графические возможности и наличие большого количества библиотек для решения различных математических задач: теории графов и сетей, линейной алгебры, дифференциальных и алгебраических уравнений, математической статистики и т.д.  Последняя, шестая версия программной системы MAPLE V делит с системой Mathematica 4.0 лидерство среди символьных математических программ. Описание систем MATLAB и MAPLE V приведено в литературе [18-21]. Ниже рассмотрено применение программных средств MATLAB и MAPLE V для решения задач анализа и синтеза систем автоматического управления.
Определение моделей и анализ линейных непрерывных систем В MATLAB
Для описания линейных динамических систем используют две основные формы описания. Первая форма – это описание систем с помощью передаточных функций. Вторая форма, модель в пространстве состояния, использует описание в виде системы обыкновенных дифференциальных уравнений. Передаточные функции. В MATLAB имеются две формы представления передаточных функций. Первая – это полиномиальная форма: В MATLAB для представления полиномов используются векторы-строки, в которых коэффициенты полинома располагаются в порядке убывания степеней: b = [1 4 3]; a = [1 6 8 0]; Здесь учитывается, что если какая-то степень пропущена, соответствующий коэффициент полинома равен нулю. Наличие в конце оператора точки с запятой исключает вывод сообщения о значении его координат. Альтернативная форма представления передаточной функции (3.1) основана на полиномах в факторной форме: Преимуществом этой формы является то, что явно указаны нули и полюса передаточной функции: нули – это корни многочлена числителя, полюса – корни многочлена знаменателя. Поэтому эта форма часто используется для предварительного анализа поведения системы. Полюса передаточной функции равны 0, –2 –4; нули равны –1, –3. Для задания этой формы представления передаточной функции в MATLAB нужно задать векторы нулей и полюсов: z = [–1 –3]; p = [0 –2 –4]; Третий параметр, коэффициент усиления (проводимости (gain)) k = 1;
Объекты типа LTI.Начиная с 5-й версии MATLAB фирма Mathworks ввела новый тип данных в Control System Toolbox. Это объект типа LTI – Linear Time Invariant System Object – объект типа "линейная автономная система". Этот объект создан для того, чтобы в одном месте хранились все свойства передаточной функции. Для создания LTI-объекта, представляющего передаточную функцию в факторной полиномиальной форме, используется команда: >>syszpk = zpk(z, p, k)
при выполнении которой для принятых значений векторов z, p и коэффициента k выводится сообщение
zero/pole/gain: (s+1) (s+3) ------------- s (s+2) (s+4) Символ “>>" означает, что система готова к принятию команд. Коэффициенты числителя и знаменателя передаточной функции можно раскрыть командой: >>[num, den] = tfdata(syszpk,'v') при выполнении которой выводится вектор num коэффициентов полинома числителя и вектор den коэффициентов знаменателя передаточной функции:
num = 0 1 4 3 den = 1 6 8 0 Объект типа LTI можно сразу задать в раскрытой полиномиальной форме с помощью команды: >>systf = tf(num, den) при выполнении которой выводится сообщение
Transfer function S^2 + 4 s + 3 ----------------- s^3 + 6 s^2 + 8 s Нули и полюса системы можно выделить командой >>[zeros, poles, gain] = zpkdata(systf,'v') zeros = -3 –1 poles = 0 –4 –2 gain = 1
Модели в пространстве состояния. В пространстве состояния непрерывная система описывается системой дифференциальных уравнений первого порядка, называемых уравнениями состояния: где Для линейных систем это описание сводится к виду где В MATLAB для описания динамических систем в пространстве состояния применяются LTI-модели подкласса ss (State space), которые основаны на линейных дифференциальных или разностных уравнениях. Для задания модели нужно задать матрицы A, B, C, D. Если матрица D отсутствует, то можно использовать присваивание syss=ss(A, B, C, D) Преобразования систем. В MATLAB преобразования между представлениями систем выполняются очень просто: sys1 = zpk(systf) – преобразование в форму zpk; sys2 = tf(sysz) – преобразование в раскрытую полиномиальную форму tf; sys3 = ss(systf) – преобразование в форму ss.
Соединения объектов типа LTI. Для создания модели нужно предварительно либо привести уравнения всей системы к форме уравнений пространства состояния, либо найти передаточные функции системы. В общем случае это довольно сложная и громоздкая задача. В то же время реальные системы автоматического управления состоят из соединенных между собой отдельных блоков (динамических звеньев), уравнения поведения которых достаточно просты. В MATLAB предусмотрена возможность программно “набирать” схему САУ путем предварительного ввода моделей простых звеньев и последующего соединения этих звеньев в единую структуру. К процедурам, осуществляющим расчет характеристик соединений отдельных звеньев, относятся: · plus (minus) – выполняет параллельное соединение указанных при обращении к процедуре звеньев; эту же процедуру можно выполнить путем обычного сложения (вычитания) идентификаторов LTI-объектов; · parallel – выполняет ту же процедуру параллельного соединения звеньев; в отличие от предыдущей процедуры для многомерных систем может осуществлять параллельное соединение лишь по некоторым входам и выходам; · mtimes – выполняет последовательное соединение указанных при обращении к процедуре звеньев; эту же процедуру можно выполнить путем обычного умножения идентификаторов LTI-объектов; · series – последовательное частичное соединение многомерных систем; · feedback – такое соединение двух звеньев, когда второе указанное звено составляет цепь обратной связи для первого звена; · inv – рассчитывает САУ, обратную указанной, т.е. такую, у которой выходы и входы поменяли местами; · vertcat – производит вертикальную конкатенкацию (сцепление) систем, т.е. такое их объединение, когда входы этих систем становятся общими, а выходы становятся независимыми; тогда число входов в результирующей системе останется таким же, как и в каждой из объединяемых систем, а число выходов будет равно сумме выходов объединяемых систем; · horzcat – производит горизонтальную конкатенкацию указанных систем, при которой выходы этих систем становятся общими, а входы добавляются. Проиллюстрируем применение некоторых из этих процедур. Например, пусть имеются две передаточные функции Для соединения этих передаточных функций можно использовать знаки обычных арифметических операций: >>G1=tf([1 1], [1 3]); >>G2=tf(10, conv([1 0],[1 2]); >>Gs = G1*G2 % последовательное соединение
Transfer function: 10 s + 10 ----------------- s^3 + 5 s^2 + 6 s
>>Gp = G1 + G2 % параллельное соединение Transfer function: s^3 + 3 s^2 + 12 s + 30 ----------------------- s^3 + 5 s^2 + 6 s Здесь для пояснения выполняемых операций используется комментарий текста программы после знака %, который не выводится на печать. Аналогичного результата можно достичь вызовом процедур соответственно Gs=mtimes(G1,G2) и Gp=plus(G1,G2). Для соединения систем с обратной связью используется функция feedback. Пусть передаточная функция разомкнутой системы имеет вид а передаточная функция регулятора в цепи обратной связи задана в виде При этом передаточная функция замкнутой системы вычисляется как Если применить обычные арифметические операции для вычисления передаточной функции замкнутой системы, то при этом могут произойти нежелательные сокращения общих множителей в числителе и знаменателе системы. Чтобы избежать этого, применяется функция feedback: >>G=tf([ 2 5 1], [1 2 3]); >>H=zpk(-2, -10, 5); >>W=feedback(G,H) % отрицательная обратная связь Zero/pole/gain: 0.18182 (s+10) (s+2.281) (s+0.2192) ----------------------------------- (s+3.419) (s^2 + 1.763s + 1.064)
Для задания положительной обратной связи используется команда feedback с дополнительным параметром, равным +1: >>W=feedback(G,H,+1) % положительная обратная связь
Анализ LTI систем. Для анализа линейных автономных систем в Control System Toolbox имеется множество функций. Перечислим некоторые из них: >>step(W) % построение переходной характеристики >>impulse(W) % построение импульсной характеристики >>bode(W) % построение ЛАХ и ЛФХ >>nyquist(W) % построение годографа Найквиста Функция pole(W) позволяет вычислить полюса системы, заданной LTI-объектом Для построения переходных процессов моделей в форме пространства состояния есть специальная функция: initial(sys, x0) Эта функция удобна для моделирования многомерных систем с регуляторами, заданными в форме
Здесь необходимо задать массив x0 – вектор-столбец начальных условий. Модель может быть как непрерывной, так и дискретной. Продолжительность моделирования определяется автоматически, так чтобы отобразить основные особенности процесса. Команда initial(sys, x0,t) позволяет явно указать продолжительность интервала моделирования Построение и анализ дискретных моделей
В состав Control System Toolbox включены две функции: для преобразования непрерывных моделей в дискретные c2d и дискретных моделей в непрерывные d2c. Реализовано несколько методов дискретизации и экстраполяции сигналов. Функция SysD=c2d(SysC, T0, ’метод’) реализует построение дискретной модели непрерывной системы SysC с периодом дискретности Используются следующие методы экстраполяции: zoh – экстраполятор нулевого порядка; foh – экстраполятор первого порядка; tustin – билинейная аппроксимация Тустена (2.55); prewarp – аппроксимация Тустена c коррекцией (2.59). В этом случае при вызове функции SysD=c2d(SysC, T0, ’prewarp’,Wc) задается частота Wc, на которой производится коррекция непрерывной и дискретной моделей. Функция SysC=d2c(SysD,’метод’) реализует построение непрерывной модели по известной передаточной функции дискретной системы, если в дискретной системе отсутствуют нулевые полюса. Построение логарифмических частотных характеристик дискретных систем. В MATLAB построение логарифмических частотных характеристик производится функцией bode. Для дискретных моделей частотная характеристика равна передаточной функции при значениях ее переменной на окружности единичного радиуса Пример.3.1. Рассмотрим непрерывную систему с передаточной функцией
Определим ее передаточную функцию в MATLAB:
>>g=tf([1 0.1 7.5],[1 0.12 9 0 0]) Transfer function: s^2 + 0.1 s + 7.5 ---------------------- s^4 + 0.12 s^3 + 9 s^2
Рис. 3.1
Перейдем от непрерывной модели к дискретной с периодом дискретности
>>gd = c2d(g, 0.5) Transfer function: 0.121 z^3 + 0.07256 z^2 + 0.06758 z + 0.1146 ---------------------------------------------- z^4 - 2.138 z^3 + 2.218 z^2 - 2.021 z + 0.9418 Sampling time: 0.5
Построим логарифмические частотные характеристики непрерывной и дискретизированной систем с помощью команды >>bode(g,’k’,gd,’k:’) Результаты вычислений приведены на рис.3.1, где в верхней части изображена логарифмическая амплитудная характеристика, в нижней – фазовая. Пунктирными линиями изображены характеристики дискретной системы. Вертикальной линией на рисунке показано значение частоты Найквиста
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 493. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . (3.1)
. (3.1) . (3.2)
. (3.2) завершает определение передаточной функции в форме полюса-нули-проводимость ZPK (pole-zero-gain). В нашем случае
завершает определение передаточной функции в форме полюса-нули-проводимость ZPK (pole-zero-gain). В нашем случае 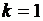 задается оператором
задается оператором
 -вектор состояния системы;
-вектор состояния системы;  -вектор входа;
-вектор входа;  -вектор выхода.
-вектор выхода. ,
, – постоянные матрицы.
– постоянные матрицы. . Тогда модель задается командой
. Тогда модель задается командой и
и  .
. ,
, .
.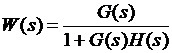 .
.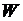 . При анализе динамических свойств систем удобна команда pzmap. После подачи команды pzmap(W) на экран выводится графическая карта расположения нулей и полюсов системы в комплексной плоскости. Символом "х" изображаются полюса системы, символом "о" – нули.
. При анализе динамических свойств систем удобна команда pzmap. После подачи команды pzmap(W) на экран выводится графическая карта расположения нулей и полюсов системы в комплексной плоскости. Символом "х" изображаются полюса системы, символом "о" – нули. . Команда initial строит реакцию на ненулевые начальные условия для модели, заданной в пространстве состояния:
. Команда initial строит реакцию на ненулевые начальные условия для модели, заданной в пространстве состояния:
 .
. и с использованием метода экстраполяции, определяемого параметром ’метод’. Если метод не указан, по умолчанию используется экстраполятор нулевого порядка.
и с использованием метода экстраполяции, определяемого параметром ’метод’. Если метод не указан, по умолчанию используется экстраполятор нулевого порядка. . Из-за периодичности частотной характеристики она рассчитывается только от нуля до частоты
. Из-за периодичности частотной характеристики она рассчитывается только от нуля до частоты 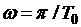 (частота Найквиста), т.е. для верхней половины единичной окружности.
(частота Найквиста), т.е. для верхней половины единичной окружности. .
.
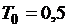 c:
c: