
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Cреднее линейное отклонениеCреднее линейное отклонение - это средний модуль отклонений значений X от среднего арифметического значения. Его можно рассчитывать по формуле средней арифметической простой - получим среднее линейное отклонение простое:
Линейный коэффициент вариации Линейный коэффициент вариации - это отношение среднего линейного отклонение к средней арифметической:
Дисперсия Дисперсия - это средний квадрат отклонений значений X от среднего арифметического значения. Дисперсию можно рассчитывать по формуле средней арифметической простой - получим дисперсию простую:
Cреднееквадратическое отклонение Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
Квадратический коэффициент вариации Квадратический коэффициент вариации - это самый популярный относительный показатель вариации:
Коэффициент вариации Мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет её средний разброс.
Коэффициент вариации равен отношению стандартного отклонения к среднему значению:
Коэффициент вариации имеет смысл использовать при ненулевых средних значениях.  Коэффициент полезен в ситуациях, когда о размерах отклонения величины можно судить, зная ее среднее значение. Иногда предлагается условная классификация вариабельности выборки на основе коэффициента вариации: при Корреляционный регрессионный анализ. Модель парной регрессии. Для целей анализа и планирования хозяйственно-экономической деятельности предприятия широко применяется корреляционно-регрессионный анализ. Корреляционно-регрессионный анализ — классический метод стохастического моделирования хозяйственной деятельности. Он изучает взаимосвязи показателей хозяйственной деятельности, когда зависимость между ними не является строго функциональной и искажена влиянием посторонних, случайных факторов. При проведении корреляционно-регрессионного анализа строят различные корреляционные и регрессионные модели хозяйственной деятельности. В этих моделях выделяют факторные и результативные показатели (признаки) [5]. Корреляционный анализ ставит задачу измерить тесноту связи между варьирующими переменными и оценить факторы, оказывающие наибольшее влияние на результативный признак. Регрессионный анализ предназначен для выбора формы связи и типа модели для определения расчетных значений зависимой переменной (результативного признака).
Методы корреляционного и регрессионного анализа используются в комплексе. Наиболее разработанной в теории и широко применяемой на практике является парная корреляция, когда исследуются соотношения результативного признака и одного факторного признака. Это — однофакторный корреляционный и регрессионный анализ. Проведем корреляционно-регрессионный анализ взаимосвязи выручки и величины оборотных средств ОАО «Новороссийский комбинат хлебопродуктов». Исходные данные для анализа представлены в следующей таблице 1: |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 348. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.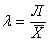 ; С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
; С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X. .
.

 .
.
 выборка вариабельна слабо, при
выборка вариабельна слабо, при 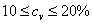 - средне, при
- средне, при 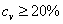 - сильно.
- сильно.