
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основная программа анализатораСтр 1 из 3Следующая ⇒ Содержание Введение. 4 ЛАБОРАТОРНАЯ РАБОТА 5 ПОСТРОЕНИЕ СИНТАКСИЧЕСКОГО АНАЛИЗАТОРА.. 5 1. Цель работы.. 5 2. Теоретическая часть. 5 2.1. Анализатор многочленов. 5 2.2. Умножение многочленов. 12 2.3. Табличный LL(1) – анализатор. 22 2.4. Табличный транслятор многочленов. 24 2.5. Реализация стека. 25 2.6. LL(1) – драйвер. 27 3. Порядок выполнения работы.. 29 4. Контрольные вопросы.. 30 Список литературы.. 31
Введение
Синтаксический анализатор (синтаксический разбор) – это часть компилятора, которая отвечает за выявление и проверку синтаксических конструкций входного языка. В задачу синтаксического анализа входит: · поиск и выделение синтаксических конструкций в тексте исходной программы; · установка типа и проверка правильности каждой синтаксической конструкции; · представление синтаксических конструкций в виде, удобном для дальнейшей генерации текста результирующей программы. В основе синтаксического анализатора лежит распознаватель текста исходной программы, построенный на основе грамматики входного языка. Как правило, синтаксические конструкции языков программирования могут быть описаны с помощью КС – грамматик, реже встречаются языки, которые могут быть описаны с помощью регулярных грамматик. К классу контекстно-свободных (КС) относятся грамматики, у которых не накладывается никаких ограничений на вид правых частей их правил, а левая часть каждого правила – единственный нетерминал. Для проектирования языков программирования используются синтаксические диаграммы, которые играют роль схемы алгоритма.  В теоретической части данной лабораторной работы рассмотрены основные этапы построения синтаксического анализатора многочленов. ЛАБОРАТОРНАЯ РАБОТА ПОСТРОЕНИЕ СИНТАКСИЧЕСКОГО АНАЛИЗАТОРА Цель работы Целью лабораторной работы является закрепление теоретических знаний и приобретение практических навыков при построении синтаксического анализатора методом рекурсивного спуска. Теоретическая часть
Анализатор многочленов
Пользуясь методом рекурсивного спуска, запрограммируем синтаксический анализатор многочленов. Будем считать, что анализатор должен просто отвечать на вопрос, является ли введенная пользователем строка правильно записанным многочленом. Язык многочленов Определим правила записи многочленов от x с постоянными целочисленными коэффициентами, с помощью синтаксических диаграмм. Примеры таких многочленов:
199 Последний пример не содержит переменной x. Условимся считать такую запись правильным многочленом нулевой степени. Чтобы запись многочленов могла быть обработана компьютерной программой (транслятором), предусмотрим возможность записи символов без надстрочных показателей степени: Построим синтаксические диаграммы, определяющие правила записи многочленов. Первой будет диаграмма для начального нетерминала, который есть не что иное как «Многочлен». Многочлен состоит из отдельных слагаемых, между которыми записываются знаки операций. Перед первым слагаемым может быть записан знак. Слагаемых должно быть не меньше одного. С учетом этого получается следующая диаграмма (рис.1).
Рис. 1. Синтаксическая диаграмма многочлена
Построим теперь диаграмму для нетерминала «Слагаемое». Одна ветвь должна соответствовать полному варианту слагаемого, когда присутствуют все его элементы: коэффициент, буква x, знак возведения в степень и сама степень. Другие ветви (обходные) должны позволять предусмотреть такие варианты слагаемого, когда нет коэффициента, буквы x и последующей степени, или только степени. При этом на диаграмме не должно появиться такого пути, пройдя по которому мы минуем как коэффициенты, так и x.
Рис. 2. Синтаксическая диаграмма слагаемого
«Целое» без знака есть последовательность, состоящая из одной и более цифр (рис.3, а). Диаграмма для нетерминала «Цифра» показана на рис.3, б. Поскольку арабские цифры используются в самых разнообразных языках, было бы неудобно каждый раз приводить диаграмму, подобную изображенной на рис. 3, б. В дальнейшем будем вместо нетерминального блока «Цифра» использовать на диаграммах овал (рис.3,в).
Рис. 3. Синтаксическая диаграмма для целого и для цифры Основная программа анализатора Вначале необходимо подготовить текст для чтения анализатором. Было бы неправильно делать так, чтобы в основной программе и распознающих процедурах отражались особенности представления входной цепочки, т.е. программировать таким образом, чтобы основные части анализатора зависели от того, считываются ли символы из файла, вводятся с терминала, извлекаются из окна редактора текста или получаются как-либо по-другому. Эта специфика будет скрыта в нескольких процедурах, которые только и будут зависеть от конкретного представления входной цепочки. Предусмотрим, что подготовка входного текста к чтению выполняется процедурой ResetText: Begin ResetText; Далее вызываем распознающую процедуру начального нетерминала, которым в нашей задаче является «Многочлен»: Polynom; Данная процедура считывает символы входной цепочки, проверяя, соответствует ли их порядок синтаксису многочленов. Если необходимо она обращается к другим распознающим процедурам. В случае, когда входная цепочка действительно содержит многочлен, процедура Polynom оставляет текущим символ, следующий за многочленом. Если при анализе многочлена обнаруживается ошибка, вызывается процедура Error, останавливающая работу анализатора. Для завершения анализа остается проверить, не содержится ли за правильно записанным многочленом во входной цепочке лишних символов: if Ch <> EOT then Error(‘Ожидается конец текста’) else WriteLn (‘Правильно’); WriteLn; end. Вспомогательные процедуры Запишем начало программы с описанием констант и переменных. Кроме глобальной переменной Ch, обозначающей текущий символ, предусмотрим глобальную переменную Pos, которая будет хранить номер этого символа во входной цепочке. program ParsePoly: const EOT = chr(0); var Ch:char; Pos: integer; Взаимодействие с входным текстом будут выполнять процедуры ResetText – готовит входную цепочку к считыванию распознавателем, и NextCh – читает очередной символ входной цепочки, перемещая его в переменную Ch. Предусмотрим чтение исходных данных из стандартного входного файла. Сообщения распознавателя будут выводиться в стандартный выходной файл (т.е. на экран). В этом случае процедура, подготавливающая текст, будет выглядеть следующим образом: procedure ResetText; begin WriteLn(‘Введите многочлен от x с целыми коэффициентами’); Pos:=0; NextCh; end; При чтении очередного символа будем игнорировать пробелы, считая их не значащими. Это позволит при записи исходного многочлена применять пробелы, например для отделения одного слагаемого от другого. procedure NextCh; begin repeat Pos:=Pos+1; if not eoln then Read(Ch) else begin ReadLn; Ch:=EOT; end; until Ch<>’ ‘; end; Такой пропуск пробелов делает их допустимыми в любом месте записи многочлена. Это не соответствует соглашениям современных языков программирования, но все же предпочтительней полного запрета пробелов. Процедура, реагирующая на ошибку, тоже зависит от соглашений по вводу и выводу. Она будет выдавать следующее сообщение на экране: procedure Error(Message:string); { Message – сообщение об ошибке} begin WriteLn(‘^’: Pos); WriteLn(‘Синтаксическая ошибка:’, Message); Halt; {Прекращение работы анализатора} end; Вывод знака ‘^’ в позиции Pos позволяет указать стрелкой на символ, вызывающий ошибку. Диалог с анализатором может быть таким: Введите многочлен от x с целыми коэффициентами 2x + 1.2 ^ Синтаксическая ошибка: Ожидается конец текста Распознающие процедуры Для каждого нетерминала грамматики многочленов, т.е. для каждой синтаксической диаграммы (рис.1-3) запишем одну распознающую процедуру. Синтаксическая диаграмма для нетерминала «Многочлен» неудобна для программирования – она содержит цикл с выходом из середины. Заменим диаграмму эквивалентной, содержащей цикл с предусловием.
Рис.4. Преобразованная диаграмма «Многочлен»
Теперь можно записать распознающую процедуру. На диаграмме три последовательных участка – в процедуре три оператора, выполняемых один за другим: if, вызов процедуры Addend, цикл while. procedure Polynom; begin if Ch in [‘+’, ‘-‘] then NextCh; Addend; {Слагаемое} while Ch in [‘+’, ‘-‘] do begin NextCh; Addend; end; end; Следующий нетерминал – «Слагаемое». Однако диаграмма, показанная на рис. 2, не разделяется на типовые фрагменты, что затрудняет программирование распознавателя. Неструктурированность обусловлена фрагментом, который помечен на рисунке знаком «?». Преобразуем диаграмму в эквивалентную, но состоящую только из совокупности типовых структур (рис.5). Для этого изобразим отдельно две ветви: одна соответствует слагаемому, начинающемуся с числа, другая – с буквы x. Фрагмент, выделенный на исходной диаграмме пунктирной рамкой, преобразуем в нетерминал «Степень».
Рис. 5. Синтаксические диаграммы «Слагаемое» и «Степень» Программирование распознающих процедур Addend (слагаемое) и Power (степень) теперь легко выполнить: диаграммы служат схемами алгоритма. procedure Addend; begin if Ch = ‘x’ then begin NextCh; Power; end else begin Number; {Целое} if Ch = ‘x’ then begin NextCh; Power; end; end; end; procedure Power; begin if Ch = ‘^’ then begin NextCh; Number; end; end; Последняя распознающая процедура – для «Целого». Ее также можно преобразовать, отделив блок, соответствующий первой цифре (обязательной), от остальных блоков.
Рис.6. Синтаксическая диаграмма «Целое»
procedure Number; begin if Ch in [‘0’.. ‘9‘] then NextCh else Error(‘Число начинается не с цифры’); while Ch in [‘0’.. ‘9‘] do NextCh; end; Распознаватель готов. Осталось только расположить процедуры в правильном порядке.
Умножение многочленов Постановка задачи Составим программу, вводящую в символьной форме два многочлена и выводящую их произведение в символьной форме в порядке убывания степеней. Пример работы программы: 1-й многочлен: 3x^2+3x-5 2-й многочлен: x^3-2x Произведение: 3x^5+3x^4-11x^3-6x^2+10x Приступим к решению поставленной задачи. Сформулируем общий план: 1. Напечатать заголовок. 2. Вывести текст первого многочлена, проанализировать его запись и преобразовать в удобную для дальнейших вычислений форму. Для выполнения действий с многочленами удобно хранить их в программе в виде массива коэффициентов, количество которых соответствует степени многочленов, а индекс каждого коэффициента равен степени соответствующего слагаемого. 3. Ввести текст второго многочлена, проанализировать его запись и преобразовать в удобную для дальнейших вычислений форму. 4. Перемножить многочлены. 5. Напечатать результат. Запишем начало программы, в котором определим необходимые константы, типы данных и переменные. program PolyMult; const nmax = 255; {Максимальная степень} type tPoly = record {Тип многочленов} n: integer; {Степень} a: array [0..nmax] of integer; {Коэффициенты} end; var P1, P2, Q: tPoly; {Сомножители и произведение} Теперь, пользуясь предварительно составленным планом, запишем основную программу. begin WriteLn (‘Перемножение многочленов’); WriteLn; WriteLn(‘Первый многочлен’); GetPoly(P1); WriteLn(‘Второй многочлен’); GetPoly(P2); MultPoly(P1, P2, Q); {Перемножение} WriteLn; WriteLn(“Произведение’); WritePoly (Q); {Печать результатов} WriteLn; end. Умножение и вывод Детализацию начнем с процедуры, которая выполняет перемножение. И входные, и выходные параметры процедуры являются многочленами, представленные в виде совокупности массива коэффициентов и величины, задающей степень многочлена, т.е. относятся к типу tPoly. Обозначим сомножители x и y, а результат – z, Запишем заголовок процедуры. procedure MultPoly(X, Y: tPoly; var Z: tPoly); Основная идея вычисления коэффициентов многочлена-произведения состоит в том, что при попарном перемножении слагаемых первого и второго многочленов получающееся произведение участвует в формировании того слагаемого многочлена-результата, степень которого равна сумме степеней сомножителей. Т.е. при перемножении i-го члена многочлена X и j-го члена многочлена Y получается величина, которая должна быть добавлена к i+j-му слагаемому Z. Такое вычисление необходимо выполнить для всех сочетаний i и j, не забыв присвоить нулевые начальные значения коэффициентам z. Получаем: procedure MultPoly(X, Y: tPoly; var Z: tPoly); var i, j: integer; begin ClearPoly(Z); for i:=0 to X.n do for j:=0 to Y.n do Z.a[i+j]:= Z.a[i+j] + X.a[i]*Y.a[j]; {Определении степени многочлена} Z.n:=nmax; while (Z.n>0) and (Z.a[Z.n]=0) do Z.n:=Z.n-1; end; Процедура ClearPoly выполняет обнуление многочлена. ClearPoly(var P:tPoly); var i:integer; begin for i:=0 to nmax do P.a[i]:=0; P.n:=0; end; Теперь рассмотрим как будет осуществляться печать многочлена. Слагаемые должны выводиться в порядке убывания степеней. Слагаемому может предшествовать знак. Коэффициент печатается, если он не равен 0 или 1. Буква x выводится для ненулевых степеней, а значение показателя степени - если эта степень больше единицы. procedure WritePoly(P: tPoly); var i:integer; begin while P do for i:=n downto 0 do begin if (a[i]>0) and (i<>n) then Write(‘ + ’) else if (a[i]<0) and (i=n) then Write(‘-‘) else if a[i]<0 then Write(‘ - ‘); if (abs(a[i])>1) or (i=0) and (a[i]<>0) or (n=0) then Write(abs(a[i])); if (i>0) and (a[i]<>0) then Write(‘x’); if (i>1) and (a[i]<>0) then Write(‘^’,i) end; end. Транслятор многочленов Реализуем теперь транслятор (процедура GetPoly), преобразующий введенную запись многочлена в массив коэффициентов. Его задача – считывать символы из входной строки, выполнять распознавание многочлена и вычислять его коэффициенты. Распознающие процедуры будут вложены внутрь GetPoly, а сама эта процедура лишь подготовит чтение входной строки, вызовет распознаватель и убедиться, что за многочленом во входной строке ничего не содержится. procedure GetPoly(var P: Poly); const EOT = chr(0); {Конец текста} var Pos: integer; {номер символа} Ch: char; {очередной символ} … {Здесь разместятся процедуры распознавателя} … begin Pos:=0; NextCh; Poly(P); if Ch<> EOT then Error (‘Ожидается конец текста’); end; Разместим на синтаксических диаграммах значки семантических процедур и определим содержание этих процедур. Семантические процедуры – это встраиваемые в распознаватель действия, предназначенные для смысловой обработки входного текста.
 
Рис. 7. Синтаксическая диаграмма многочлена с семантическими процедурами
Перед началом обработки массив коэффициентов многочлена заполняется нулями, а его степень принимается равной нулю. Эту работу выполняет семантическая процедура
Каждое слагаемое многочлена имеет вид
P.a[k]:= P.a[k] + a else P.a[k]:= P.a[k] – a; Было бы неправильно просто записывать значение коэффициента в a[k], поскольку в записи многочлена могут быть несколько членов с одинаковой степенью x – синтаксис этого не запрещает. Складывая или вычитая каждый коэффициент с предыдущей суммой, транслятор как бы приводит подобные. Определение степени n многочлена P выполняет семантическая процедура
while (P.n >0) and (P.a[P.n] = 0) do P.n:=P.n-1; Теперь пользуясь диаграммой и вставляя в текст анализатора в соответствующих местах определенные семантические процедуры, запишем распознаватель многочленов. procedure Poly(var P: tPoly); var a: integer; {Модуль коэффициента} k: integer; {Степень слагаемого} Op : char; {Знак операции} begin ClearPoly(P); {P3} if Ch in [‘+’, ‘-‘] then begin Op:=Ch; {P4} NextCh; end else Op:=’+’; {P5} Addend(a, k,) if Op = ‘+’ then {P6} P.a[k]:= P.a[k] + a else P.a[k]:= P.a[k] – a; while Ch in [‘+’,’-‘] do begin Op:=Ch {P4} NextCh; Addend(a, k,) if Op = ‘+’ then {P6} P.a[k]:= P.a[k] + a else P.a[k]:= P.a[k] – a; end; P.n:= nmax; {P7} while (P.n >0) and (P.a[P.n] = 0) do P.n:=P.n-1; end; Задача транслятора слагаемого состоит в определении коэффициента a и степени k. В соответствии с этим предусмотрим следующие семантические процедуры (рис. 8)
Рис. 8 Синтаксическая диаграмма слагаемого с семантическими процедурами
Процедура Если коэффициент отсутствует, он принимается равным единице.
Значение степени либо берется равным вычисленному распознавателем степени, либо нулевым, если в записи слагаемого отсутствует x.
Запишем теперь распознаватель – транслятор для слагаемого. procedure Addend (var a, k : integer); begin if Ch in [‘0’..’9’] then begin Number(a); {P8} if Ch = ‘x’ then begin NextCh; Power(k); {P10} end else k:=0 {P11} end else if Ch = ‘x’ then begin a:=1; {P9} NextCh; Power(k); {P10} end else Error(‘ Ожидается число или “x”’); end; Реализация распознавателя нетерминала «Степень» выполняется по соответствующей синтаксической диаграмме.
Рис. 9. Синтаксическая диаграмма степени с семантическими процедурами
Чтобы защитить программу от ошибки при обращении к массиву коэффициентов, в процедуре if p>nmax then Error (‘Слишком большая степень’); Семантическая процедура procedure Power (var p: integer); begin if Ch = ‘^’ then begin NextCh; Number(p); {P12} if p>nmax then Error (‘Слишком большая степень’); end else p:=1; {P13} end; |
||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 359. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 .
.







 и
и  отвечают за запоминание знака перед слагаемым. Знак сохраняется в локальной переменной Op.
отвечают за запоминание знака перед слагаемым. Знак сохраняется в локальной переменной Op. . Транслятор слагаемого вычислит значения коэффициента a и степени k. Получив эти значения, семантическая процедура
. Транслятор слагаемого вычислит значения коэффициента a и степени k. Получив эти значения, семантическая процедура 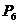 в зависимости от знака добавит или отнимет значение a из k –й ячейки массива коэффициентов:
в зависимости от знака добавит или отнимет значение a из k –й ячейки массива коэффициентов: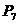 .
.
 присваивает коэффициенту a значение, равное величине целого числа, которое вычисляет транслятор целого. В программе это будет реализовано подстановкой переменной a в качестве параметра при вызове процедуры Number.
присваивает коэффициенту a значение, равное величине целого числа, которое вычисляет транслятор целого. В программе это будет реализовано подстановкой переменной a в качестве параметра при вызове процедуры Number.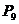 : a:=1;
: a:=1; : k:= значение степени;
: k:= значение степени; : k:=0;
: k:=0;
 предусмотрен контроль величины показателя степени. Вычисляемая степень обозначается p.
предусмотрен контроль величины показателя степени. Вычисляемая степень обозначается p. : p:=1;
: p:=1;