
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Порядок выполнения работыСтр 1 из 5Следующая ⇒ ЛАБОРАТОРНАЯ РАБОТА № 2 «ИССЛЕДОВАНИЕ СПЕКТРА СИГНАЛА И ГЕНЕРАЦИЯ» Цель и задачи лабораторной работы Целью лабораторной работы является экспериментальное изучение основных положений преобразований Фурье. Определение спектрального анализа периодических сигналов. Задачами лабораторной работы являются: - проведение спектрального анализа периодических сигналов (прямое преобразование Фурье); - генерация периодических сигналов по его гармоническим составляющим (обратное преобразование Фурье). Теоретическая часть Спектральный анализ периодических сигналов. Анализ периодических сигналов и радиотехнических цепей производится как временным способом, так и спектральным, который основан на разложении сигналов в тригонометрический ряд Фурье. Цель временного анализа — определить изменение формы сигнала по отклику (реакции) цепи на оказываемое на нее воздействие, а спектрального – выявить изменения сигнала по преобразованию спектра данной цепью. Гармонический (спектральный) анализ – это раздел математики, который изучает возможности представления функций в виде тригонометрических рядов и интегралов. Основным понятием в гармоническом анализе является гармоническое колебание, которое математически можно записать следующим образом:
где А, В гармоническом анализе вводится понятие n–й гармоники гармонического колебания частоты 
где В теории связи функциями являются различные сигналы. Под спектром сигнала понимают совокупность его гармонических составляющих. Основа спектрального анализа периодических сигналов – ряд Фурье. Любой периодический сигнал можно представить в виде бесконечного суммирования гармонических колебаний (гармоник):
где
Рисунок 3.1 - Четные (а) и нечетные (б) функции. Из формул для коэффициентов ряда Фурье следует, что четный сигнал имеет только косинусоидальные (рис. 3.1,а), а нечетный – только синусоидальные слагаемые (рис. 3.1,б). Все это приводит к выводу, что спектральная функция «четного» сигнала содержит только постоянную и косинусные составляющие, а «нечетного» сигнала - только синусные составляющие; если же сигнал выражается произвольной функцией времени, то в нем имеются оба ряда составляющих: и синусный, и косинусный. Характерно, что спектр периодических сигналов не сплошной, а линейчатый, т.е. между соседними линиями спектра имеются «просветы» шириной в частоту следования сигнала F = 1/T.
Из этого следует, что периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармоник с частотами Каждую гармонику можно описать ее амплитудой
Так что
Подставив эти выражения в (3.3), получим эквивалентную форму ряда Фурье:
На рисунке 3.2, а показано, что если в любой момент времени t сложить три синусоидальных напряжения U1, U2, U3, имеющих соответственно периоды T1, T2 = T1/2, T3 = T1/3, амплитуды U1m, U2m, U3m и начальные фазы
Рисунок 3.2 - Диаграммы периодического несинусоидального сигнала Все гармонические составляющие образуют в совокупности спектр сигнала, изображаемый двумя диаграммами, из которых одна называется амплитудно-частотным спектром, а другая – фазо-частотным. На этих диаграммах ось абсцисс образует шкалу частот В радиотехнических устройствах сигнал подвергается различным формам обработки. Для того чтобы рассчитать результат этих преобразований, используется комплексная форма ряда Фурье. Эти преобразования имеют формальный характер и связаны с применением комплексной формы для представления функции вещественной переменной. Поэтому при проведении расчетов реальный сигнал можно представить в виде функции комплексной переменной, преобразовав его соответствующим образом, а затем снова перейти к вещественному представлению:
где
Входящая в формулу (2.5) комплексная амплитуда Отсюда видно, что комплексные амплитуды Отрицательные частоты, которые вводятся для представления реального сигнала s(t) комплексным рядом Фурье, носят формальный характер и не имеют никакого физического смысла. Порядок выполнения работы |
||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 180. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,
 ,
,  - соответственно амплитуда, циклическая частота, начальная фаза колебания.
- соответственно амплитуда, циклическая частота, начальная фаза колебания. основного тона
основного тона  ,
,
 ,
,  ,
,  - амплитуда, циклическая частота, начальная фаза n–й гармоники основного тона
- амплитуда, циклическая частота, начальная фаза n–й гармоники основного тона  ,
,
 соответствует постоянной составляющей сигнала, а
соответствует постоянной составляющей сигнала, а  и
и  представляют амплитуды косинусоидальных и синусоидальных гармоник сигнала соответственно.
представляют амплитуды косинусоидальных и синусоидальных гармоник сигнала соответственно.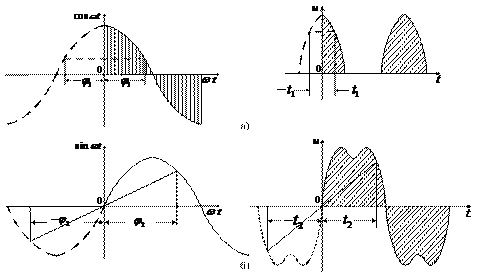
 =
=  - циклическая частота первой гармоники, величина которой обратно пропорциональная периоду сигнала.
- циклическая частота первой гармоники, величина которой обратно пропорциональная периоду сигнала. (n=1, 2, 3…), кратными основной частоте последовательности.
(n=1, 2, 3…), кратными основной частоте последовательности. и начальной фазой
и начальной фазой  . Для этого коэффициенты ряда Фурье записываются в виде:
. Для этого коэффициенты ряда Фурье записываются в виде: ,
, 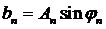 .
. ,
,  .
. .
.
 , то получится несинусоидальное напряжение U с таким же периодом T, как и у первой гармоники (T= T1).
, то получится несинусоидальное напряжение U с таким же периодом T, как и у первой гармоники (T= T1).
 , а на оси ординат откладываются отрезки, длина которых пропорциональна амплитуде Unm (для амплитудно-частотного спектра, рис. 3.2,б) или начальной фазе
, а на оси ординат откладываются отрезки, длина которых пропорциональна амплитуде Unm (для амплитудно-частотного спектра, рис. 3.2,б) или начальной фазе  (для фазо-частотного спектра, рис. 3.2, в) соответствующей n-й гармоники.
(для фазо-частотного спектра, рис. 3.2, в) соответствующей n-й гармоники.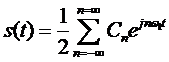 ,
,
 .
.
 связана с
связана с  и
и  следующими соотношениями:
следующими соотношениями: ,
,  .
. являются взаимно сопряженными комплексными величинами. Четность модуля
являются взаимно сопряженными комплексными величинами. Четность модуля