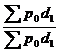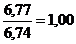Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Индивидуальные и общие индексы в форме агрегатной. Система взаимосвязанных индексов.Средние индексы. Система индексов в анализе динамики среднего уровня.
Индекс – особый вид относительных величин, который характеризует соотношение экономических явлений, совокупностей, которые состоят из качественно однородных, но непосредственно не суммируемых элементов. В процессе анализа часто приходится иметь дело с совокупностями, которые состоят из не суммируемых элементов. С такого рода совокупностями сталкиваемся, когда необходимо охарактеризовать изменение объемов произведенной, реализованной или потребленной разнородной продукцией, товара в натуральной форме. Но объем такой продукции или товара в стоимостном выражении может сопоставляться, так как несовместимость натуральной формы тут исключена. С помощью индексов в статистическом анализе решают следующие задачи: - определение средних изменений сложных, непосредственно не суммарных явлений, совокупностей во времени и в динамики; - оценка средней степени выполнения договора по совокупности в целом или отдельных ее частях и использование индексов для установления договорных заданий; - установление средних соотношений по территории; - определение роли отдельных факторов, которые связаны с результативным фактором, когда индексы выступают как аналитический способ. Индексы в анализе характеризуют:  - изменение явлений, их динамику, как относительные величины и выражаются в коэффициентах (разах) или процентах; - абсолютное изменение явлений в целом, а так же под влиянием отдельных факторов. Классификация индексов и их виды: - индивидуальные (i) и общие индексы (I) в зависимости от степени охвата элементов совокупности; - общие (групповые) индексы в форме агрегатной и средней в зависимости от методики расчета; - индексы количественных и качественных показателей в зависимости от того, изменение каких показателей они характеризуют; - индексы постоянного и переменного состава в зависимости от количества факторов, которые влияют на результаты расчетов. Каждый индекс включает данные за два периода: отчетный (сравниваемый, текущий) – подстрочный значок 1 и базисный, который используется как база сравнения – подстрочный значок 0. Таким образом, индекс это – относительный показатель, получающийся в результате сравнения двух абсолютных величин, характеризующих уровень изучаемого явления для двух разных периодов.
Индекс как относительную величину получают путем соотношения соответствующих показателей отчетного и базисного периодов. Основным элементом индексного отношения является индексируемая величина, под которой понимается значение признака статистической совокупности, изменение которого является объектом изучения. Так, при изучении изменения цены индексируемой величиной является цена единицы товара и т.п. Пример: приведены данные о реализации товаров кондитерским отделом продовольственного магазина.
Индивидуальные индексы характеризуют изменение отдельных единиц статистической совокупности. Формулы индивидуальных индексов: - цены: ip = - количества: iq = - отдельного вида товарооборота продукции или товара: ipq = Пример: рассчитаем индивидуальные индексы по приведенным выше формулам:
Цена на печенье снизилась на 1%, количество реализованной продукции увеличилось на 6%, что привело к росту товарооборота на 5%. Товарооборот конфет снизился на 8% за счет уменьшения количества реализованной продукции на 11% и роста цены на 4%. Общие индексы выражают сводные результаты совместного изменения всех единиц, образующих статистическую совокупность. Важнейшей особенностью общих индексов является то, что они обладают синтетическими и аналитическими свойствами. Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение (агрегирование) в целое разнородных единиц совокупности. Аналитические свойства индексов состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя. В общих индексах сопоставляются суммы стоимости непосредственно не суммируемых совокупностей, так как стоимостная форма выражения приводит не суммируемые по физическому состоянию товары, продукцию к суммируемому виду. Формулы общих индексов: - товарооборот в действующих ценах: Ipq = Ipq – общий стоимостной индекс товарооборота в действующих ценах;
Разница между числителем и знаменателем этого индекса – это абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным: ∆pq = ∆pq - абсолютное изменение товарооборота в неизменных, базисных ценах.
- товарооборота в неизменных, базисных (сопоставимых) ценах: Iq = Iq – общий индекс товарооборота в неизменных (базисных) ценах;
Разница между числителем и знаменателем этого индекса показывает абсолютное изменение товарооборота за счет изменения количественного (экстенсивного) фактора: ∆pq (q) = ∆pq (q) – абсолютное изменение товарооборота за счет физического объема, количества товара (продукции).
Разница между числителем и знаменателем индекса цен Пааше показывает абсолютное изменение товарооборота за счет изменения цен (качественного, интенсивного) фактора и рассчитывается по формуле: ∆pq (p) = ∆pq(p) – абсолютное изменение товарооборота за счет цены. Для проверки расчетов используют формулу: ∆pq = ∆pq (p) + ∆pq (q) = Пример: рассчитаем общие индексы в форме агрегатной по имеющимся данным и определим абсолютное изменение товарооборота в целом, а так же за счет изменения цены и количества реализованной продукции. Товарооборот по анализируемым продуктам в целом снизился на 1%или 41,75 грн. это произошло за счет сокращения количества реализуемой продукции на 3% или 82 грн. Рост цены на 1% привел к увеличению товарооборота на 40,25 грн.
При построении общих индексов в форме агрегатной придерживаются следующих принципов: 1. В числителе и знаменатели после значка суммы на первом месте всегда стоит показатель, изменение которого характеризует индекс. Этот символ носит название изменяемого, индексованного показателя, который изучает содержание индекса, так как стоит под строчкой в индексе; 2. В числителе и знаменателе индексов после знака индекса на втором месте всегда стоит показатель неизменяемый, который при построении формулы играет роль весов и на результаты расчетов, величину индекса не оказывает влияния. Мы знаем, что между отдельными явлениями общественной жизни существует определенная взаимосвязь и взаимозависимость. Так цена единицы реализованной продукции умноженная на его количество дает стоимость. Зависимость и взаимосвязь между отдельными экономическим явлениями отражается во взаимосвязях и зависимостях между соответствующими статистическими показателями, в том числе и между индексами, как особым видом относительных величин. Так имеет место взаимосвязь абсолютных показателей: P x Q = PQ Такая же взаимосвязь существует и между индексами этих абсолютных показателей. Общий вид формулы взаимосвязи индексов, которые нами рассмотрены: Ip x Iq = Ipq или Ip = Ipq / Iq или Iq = Ipq / Ip
В статистической теории существует две системы индексной взаимосвязи в соответствии с их общей формулой Первая система, в которую входит индекс цен Пааше имеет следующий вид:
Вторая система, в которую входит индекс цен Ласпейреса соответственно имеет вид:
Пример: рассмотрим взаимосвязь индивидуальных и общих индексов:
В случае отсутствия информации для построения индексов в агрегатной форме, они могут быть построены в форме средних из индивидуальных индексов. Индекс средний арифметический. В качестве основной исходной формы общего индекса физического объема мы брали агрегатный индекс, взвешенный по неизменным ценам базисного периода: Iq = Для преобразования используем формулу индивидуального индекса объема продукции iq = Iq = В таком виде индекс физического объема продукции выступает как средняя арифметическая величина из индивидуальных индексов, взвешенных по стоимости продукции базисного периода в неизменных, базисных ценах. Практика ведения учета реализованной продукции делает невозможным непосредственное применение агрегатной формы индекса Ласпейреса. Но при наличии информации об индивидуальных индексах цен возможно преобразование первоначальной формулы в среднюю арифметическую. Это осуществляется путем замены Ip = Пример: рассчитаем рассмотренные средние арифметические индексы:
Индекс средний гармонический. Агрегатный индекс может быть выражен и через средний гармонический индекс. Рассмотрим на примере общего индекса цен. Для этого через индивидуальный индекс цены выразим цену базисного периода: Ip = В таком виде индекс цен выступает как средняя гармоническая величина из индивидуальных индексов цен, взвешенных по сумме фактического товарооборота отчетного периода. При наличии информации об индивидуальных индексах физического объема и фактической стоимости продукции в текущем периоде общий индекс физического объема продукции определяется по средней гармонической формуле:
Пример: рассчитаем рассмотренные средние гармонические индексы:
Часто с помощью индексов изучают динамику средних уровней качественных показателей: средней цены, среднего уровня производительности труда, средней скорости обращения товаров и т.д. Пример: рассмотрим систему индексов в анализе динамике среднего уровня на следующих данных о цене на мясо на рынках города:
Расчет средней цены производится по следующим формулам: - средняя цена базисного периода: - средняя цена отчетного периода: - средняя условная цена: Пример: произведем расчет средних цен:
Средняя цена в отчетном периоде по сравнению с базисным сократилась, в то время как средняя условная цена возросла.
Рассмотрим принципы построения этих индексов на примере средней цены. В общем виде система имеет следующий вид:
Ip переменного состава = Ip постоянного состава х I структурных изменений в объеме реализованных товаров,
Кроме относительного изменения среднего показателя – средней цены, и меры влияния на нее отдельных факторов в относительном выражении, эта система индексов дает возможность рассчитать в абсолютном выражении изменение средней цены. Ip переменного состава – индекс средней цены, который показывает в относительном выражении изменение средней цены по влиянием двух отдельных факторов: изменение цены у отдельных продавцов (качественный фактор); изменение структуры реализации продукции (количественный фактор): Ip переменного состава = Изменение цены в целом: ∆
Ip постоянного состава – индекс постоянного (фиксированного) состава, который показывает в относительном выражении меру влияния цены у отельных продавцов на среднюю цену: Ip постоянного состава = Изменение цен у отдельных продавцов: ∆
I структурных изменений – индекс влияния структурных изменений в составе реализованного товара с различным уровнем цен, который показывает в относительном выражении влияние второго фактора на среднюю цену:
I структурных изменений = Изменение структуры состава реализованной продукции у отдельных продавцов с разным уровнем цен: ∆
Проверка верности расчетов: ∆ Пример: произведем расчет индексов, характеризующих динамику среднего уровня цены.
Средняя цена на мясо уменьшилась на 0,42 грн. или 6%. Это произошло под влиянием двух факторов: - снижения цен на отдельных рынках на 0,45грн. или 7%; - структурных изменений в реализации продукции. За счет этого средняя цена возросла на 0,03грн. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 277. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Важное значение в статистических исследованиях коммерческой деятельности имеет индексный метод. Полученные на основе этого метода показатели используются для характеристики развития анализируемых явлений во времени, по территории, изучении структуры и взаимосвязей.
Важное значение в статистических исследованиях коммерческой деятельности имеет индексный метод. Полученные на основе этого метода показатели используются для характеристики развития анализируемых явлений во времени, по территории, изучении структуры и взаимосвязей.  Нами будут рассмотрены принципы построения индексов, которые характеризуют динамику сложных явлений. Для формализации и сокращения их записи необходимо ввести условные обозначения:
Нами будут рассмотрены принципы построения индексов, которые характеризуют динамику сложных явлений. Для формализации и сокращения их записи необходимо ввести условные обозначения: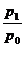
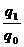

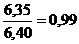
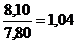
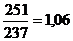
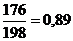

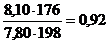
 ,где
,где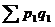 ,
,  - сумма товарооборота по нескольким видам продукции соответственно в отчетном и базисном периодах;
- сумма товарооборота по нескольким видам продукции соответственно в отчетном и базисном периодах; , где
, где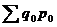 - сумма стоимости товарной массы базисного периода в ценах того же периода.
- сумма стоимости товарной массы базисного периода в ценах того же периода.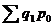 -
- 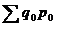 , где
, где
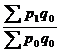
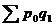 , где
, где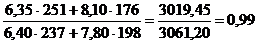

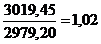

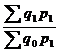 =
= 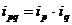

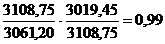
 Как уже отмечалось, для расчета общих индексов в форме агрегатной, необходимы данные и количестве отдельных товаров в натуральных измерителях.
Как уже отмечалось, для расчета общих индексов в форме агрегатной, необходимы данные и количестве отдельных товаров в натуральных измерителях. . Произведем замену в числителе общего индекса и тогда он примет вид:
. Произведем замену в числителе общего индекса и тогда он примет вид:
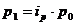 .
.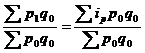
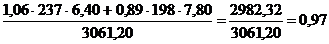
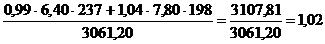
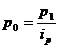 . Произведем соответствующую замену в общем индексе в форме агрегатной:
. Произведем соответствующую замену в общем индексе в форме агрегатной: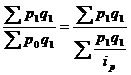
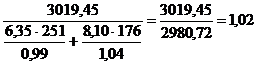
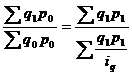


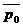 =
= 
 =
= 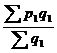
 =
= 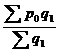
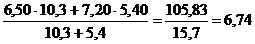

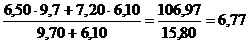
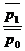 =
= 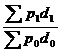
 =
=  =
= 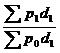
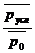 =
=