
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Результаты работы программы.К У Р С О В О Й П Р О Е К Т Дисциплина: Численные методы. Тема: «Решение краевой задачи для обыкновенного дифференциального уравнения второго порядка».
Выполнил студент гр. 23431/5 _______________ Жолдасов И.У. Руководитель _______________ ассистентСафонов А.C. «____» _________ 2017 г. Оглавление 1. Решение краевой задачи для обыкновенного дифференциального уравнения второго порядка 3 1.1. Постановка задачи 3 1.2. Вывод разностной схемы для уравнения и граничных условий 3 1.3. Полученная разностная схема 4 1.4. Вывод выражения для главного члена погрешности аппроксимации уравнения и граничных условий 5 1.5. Тестовые задачи с нулевой и ненулевой погрешностью аппроксимации 8 1.6. Текст программы 9 1.7. Результаты работы программы 16 1.8. Выводы 18
Решение краевой задачи для обыкновенного дифференциального уравнения второго порядка
1.1. Постановка задачи:
1.2. Вывод разностной схемы для уравнения и граничных условий:
Найдем разностную схему для
Проинтегрируем по формуле средних прямоугольников:
Оценив последние два интеграла таким способом:
1.3. Полученная разностная схема:
Вывод выражения для главного члена погрешности аппроксимации уравнения и граничных условий.

Тестовые задачи с нулевой и ненулевой погрешностью аппроксимации. Для того, чтобы убедиться в том, что выведенная разностная схема действительно аппроксимирует решение с порядком
Остаётся решить задачу:
Так как погрешность аппроксимации в этой задаче нулевая, следует ожидать возрастания погрешности решения с увеличением количества отрезков разбиения вследствие возрастания погрешности решения системы увеличивающегося порядка методом прогонки.
В этой задаче следует ожидать уменьшения нормы погрешности решения в 4 раза с увеличением количества отрезков разбиения в 2 раза, т.к. выведенная разностная схема имеет второй порядок аппроксимации. Текст программы . Программа для тестовой задачи с нулевой погрешностью аппроксимации:
#include <iostream> #include <fstream> #include <cmath> #include <imsl.h>
using namespace std;
doublemax_val(double *a, int n) { double s = a[0]; for (inti = 1; i< n; i++) if (a[i] > s) s = a[i]; return s; }
double f(double r) //функция f иззадания { return (2.*r*r – 2.); }
doubleu(doubler) //искомая тестовая функция { return (r*r + 1.); }
doublekf(doubler) //функцияkиззадания { return 1; }
int main() { ofstream out("output.txt");
intndata[] = {10, 20, 40, 80, 160}; double x = 0.0, y = 2.0; doubleepsp, eps, cond; constintnlca = 1, nuca = 1;
for (int k = 0; k < 5; k++) { int N = ndata[k]; out<< "Числоотрезковвразбиении N = " << N <<endl; out<<endl;
double r[N], r_2[N], r_1[N], MAX[N] ; double a[N], b[N], c[N]; double A[N*(nlca+nuca+1)], *v, d[N]; double h = (double)(y - x)/(double)N;
for (inti = 0; i< N + 1; i++) r[i] = x + (double)i*h;
for (inti = 1; i< N + 1; i++) r_1[i]=(r[i-1] + r[i])/2;
for (inti = 0; i< N; i++) r_2[i]=(r[i] + r[i+1])/2;
for (inti = 1; i< N - 1; i++) { c[i] = -(r_2[i]*kf(r_2[i]) + r_1[i]*kf(r_1[i]))/(h*h*r[i]) - 2.; d[i] = -f(r[i]); } for (inti = 1; i< N; i++) { a[i-1] = (r_1[i]*kf(r_1[i]))/(r[i]*h*h); b[i+1] = (r_2[i]*kf(r_2[i]))/(r[i]*h*h); }
b[0] = 0; b[1]= (4.*kf(r_2[0]))/(h*h); c[0]= -(4.*kf(r_2[0]))/(h*h) - 2.; d[0]= -f(0);
a[N-1]= 0; c[N-1]= -(r_2[N-1]*kf(r_2[N-1]) + r_1[N-1]*kf(r_1[N-1]))/(h*h*r[N-1]) - 2.; d[N-1]= -f(r[N-1]) - (5.*r_1[N]*kf(r_1[N]))/(r[N-1]*h*h);
for (int j = 0; j < N; j++) { A[j] = b[j]; A[N + j] = c[j]; A[2*N + j] = a[j]; }
v = imsl_d_lin_sol_gen_band (N, A, nlca, nuca, d, IMSL_CONDITION, &cond, 0);
out<< "Число обусловленности: " <<cond<<endl; out<<endl;
for (inti = 0; i< N; i++) { MAX[i] = fabs(u(r[i]) - v[i]); } eps = max_val(MAX, N); out<< "Нормаошибки: " << eps <<endl; out<<endl;
if (k > 0) { out<< "epsilon(N = " <<ndata[k - 1] << ")/epsilon(N = "<<ndata[k] << ") = " << eps/epsp<<endl; }
epsp = eps;
out<<endl; out<<endl; out<< "_____________________________________________" <<endl; out<<endl; } return 0; } Программа для тестовой задачи с ненулевой погрешностью аппроксимации: #include <iostream> #include <fstream> #include <cmath> #include <imsl.h>
using namespace std;
doublemax_val(double *a, int n) { double s = a[0]; for (inti = 1; i< n; i++) if (a[i] > s) s = a[i]; return s; }
double f(double r) //функция f иззадания { return (1.5*pow(r, 3) - 6.75*r - 2.); }
doubleu(doubler) //искомаятестоваяфункция { return (0.75*pow(r, 3) - 1.); }
doublekf(doubler) //функцияkиззадания { return 1.; }
int main() { ofstream out("output.txt");
intndata[] = {10, 20, 40, 80, 160}; double x = 0.0, y = 2.0; doubleepsp, eps, cond; constintnlca = 1, nuca = 1;
for (int k = 0; k < 5; k++) { int N = ndata[k]; out<< "Числоотрезковвразбиении N = " << N <<endl; out<<endl;
double r[N], r_2[N], r_1[N], MAX[N] ; double a[N], b[N], c[N]; double A[N*(nlca+nuca+1)], *v, d[N]; double h = (double)(y - x)/(double)N;
for (inti = 0; i< N + 1; i++) r[i] = x + (double)i*h;
for (inti = 1; i< N + 1; i++) r_1[i]=(r[i-1] + r[i])/2;
for (inti = 0; i< N; i++) r_2[i]=(r[i] + r[i+1])/2;
for (inti = 1; i< N - 1; i++) { c[i] = -(r_2[i]*kf(r_2[i]) + r_1[i]*kf(r_1[i]))/(h*h*r[i]) - 2.; d[i] = -f(r[i]); } for (inti = 1; i< N; i++) { a[i-1] = (r_1[i]*kf(r_1[i]))/(r[i]*h*h); b[i+1] = (r_2[i]*kf(r_2[i]))/(r[i]*h*h); }
b[0] = 0; b[1]= (4.*kf(r_2[0]))/(h*h); c[0]= -(4.*kf(r_2[0]))/(h*h) - 2.; d[0]= -f(0);
a[N-1]= 0; c[N-1]= -(r_2[N-1]*kf(r_2[N-1]) + r_1[N-1]*kf(r_1[N-1]))/(h*h*r[N-1]) - 2.; d[N-1]= -f(r[N-1]) - (5.*r_1[N]*kf(r_1[N]))/(r[N-1]*h*h);
for (int j = 0; j < N; j++) { A[j] = b[j]; A[N + j] = c[j]; A[2*N + j] = a[j]; }
v = imsl_d_lin_sol_gen_band (N, A, nlca, nuca, d, IMSL_CONDITION, &cond, 0);
out<< "Число обусловленности: " <<cond<<endl; out<<endl;
out<< "Векторрешений:" <<endl; for(inti = 0; i< N; i++) { out<<i<< "\t" << v[i]; out<<endl; } out<<endl;
for (inti = 0; i< N; i++) { MAX[i] = fabs(u(r[i]) - v[i]); } eps = max_val(MAX, N); out<< "Нормаошибки: " << eps <<endl; out<<endl; if (k > 0) { out<< "epsilon(N = " <<ndata[k - 1] << ")/epsilon(N = "<<ndata[k] << ") = " <<epsp/eps <<endl; } epsp = eps; out<<endl; out<<endl; out<< "_____________________________________________" <<endl; out<<endl; } return 0; } Программа для задачи, полученной от преподавателя: #include <iostream> #include <fstream> #include <cmath> #include <imsl.h>
using namespace std;
doublemax_val(double *a, int n) { double s = a[0]; for (inti = 1; i< n; i++) if (a[i] > s) s = a[i]; return s; }
double f(double r) //функция f иззадания { return (2*(r*r - 3*r - 1)); }
doubleu(doubler) //искомаятестоваяфункция { return 1; }
doublekf(doubler) //функцияkиззадания { return (r + 1.); }
int main() { ofstream out("output.txt");
intndata[] = {10, 20, 40, 80, 160}; double x = 0.0, y = 2.0; doublecond; constintnlca = 1, nuca = 1;
for (int k = 0; k < 5; k++) { int N = ndata[k]; out<< "Числоотрезковвразбиении N = " << N <<endl; out<<endl;
double r[N], r_2[N], r_1[N]; double a[N], b[N], c[N]; double A[N*(nlca+nuca+1)], *v, d[N]; double h = (double)(y - x)/(double)N;
for (inti = 0; i< N + 1; i++) r[i] = x + (double)i*h;
for (inti = 1; i< N + 1; i++) r_1[i]=(r[i-1] + r[i])/2;
for (inti = 0; i< N; i++) r_2[i]=(r[i] + r[i+1])/2;
for (inti = 1; i< N - 1; i++) { c[i] = -(r_2[i]*kf(r_2[i]) + r_1[i]*kf(r_1[i]))/(h*h*r[i]) - 2.; d[i] = -f(r[i]); } for (inti = 1; i< N; i++) { a[i-1] = (r_1[i]*kf(r_1[i]))/(r[i]*h*h); b[i+1] = (r_2[i]*kf(r_2[i]))/(r[i]*h*h); }
b[0] = 0; b[1]= (4.*kf(r_2[0]))/(h*h); c[0]= -(4.*kf(r_2[0]))/(h*h) - 2.; d[0]= -f(0);
a[N-1]= 0; c[N-1]= -(r_2[N-1]*kf(r_2[N-1]) + r_1[N-1]*kf(r_1[N-1]))/(h*h*r[N-1]) - 2.; d[N-1]= -f(r[N-1]) - (5.*r_1[N]*kf(r_1[N]))/(r[N-1]*h*h);
for (int j = 0; j < N; j++) { A[j] = b[j]; A[N + j] = c[j]; A[2*N + j] = a[j]; }
v = imsl_d_lin_sol_gen_band (N, A, nlca, nuca, d, IMSL_CONDITION, &cond, 0);
out<< "Число обусловленности: " <<cond<<endl; out<<endl;
out<< "Векторрешений:" <<endl; for(inti = 0; i< N; i++) { out<<i<< "\t" << 2.*(float)i/(float)N << "\t" << v[i]; out<<endl; } out<<endl; } return 0; } Результаты работы программы.
Таблица результатов работы программы для задачи, полученной от преподавателя:
График приближенного решения для разбиения на 20 отрезков
Выводы. Из результатов для тестовой задачи с нулевой погрешностью аппроксимации видно, что чебышёвская норма погрешности решения возрастает с увеличением Из результатов для тестовой задачи с ненулевой погрешностью аппроксимации видно, что при удвоении количества отрезков разбиения погрешность уменьшается в четыре раза; значит, порядок аппроксимации Получено численное решение поставленной краевой задачи. Результаты ее решения также подтверждают теоретически полученные формулы погрешности аппроксимации.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 302. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

















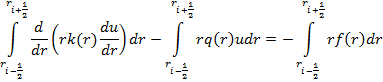

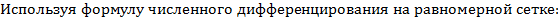








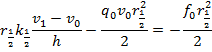

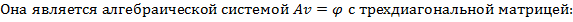









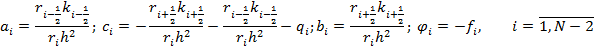



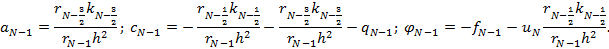





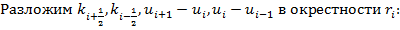



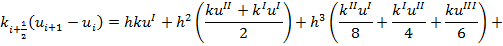



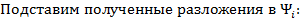






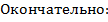





















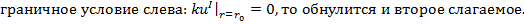


 и сходится к решению уравнения, построим две тестовые задачи, для которых известно аналитическое решение и его можно сравнить с решением, получаемым решением
и сходится к решению уравнения, построим две тестовые задачи, для которых известно аналитическое решение и его можно сравнить с решением, получаемым решением  , и проанализировать полученные данные.
, и проанализировать полученные данные.





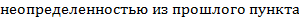



















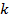








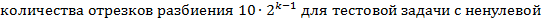















 выведенной разностной схемы действительно равен двумкак на левой границе, так и во внутренних точках отрезка.
выведенной разностной схемы действительно равен двумкак на левой границе, так и во внутренних точках отрезка.