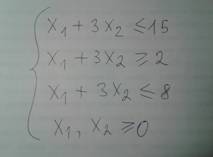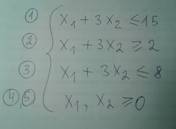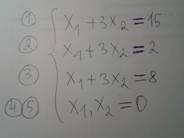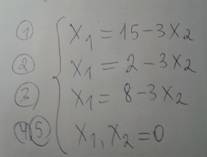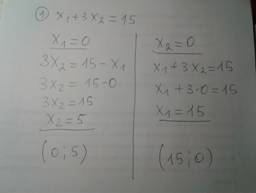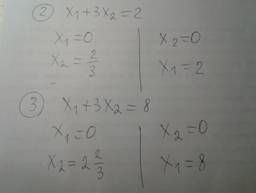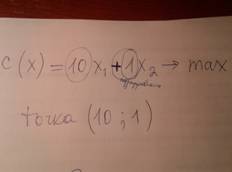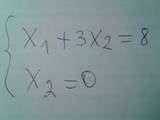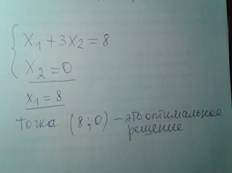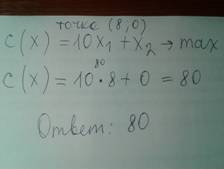Для четверки еще всего лишь неправильно вторую останется порешать)»

ПЛАН РЕШЕНИЯ ПЕРВОЙ ЗАДАЧИ ПО МАТЕМАТИЧЕСКИМ МЕТОДАМ.

«Я верю, вы справитесь)) Просто делайте по алгоритму)
Только попробуйте теперь не решить!!!!!)
Оставьте бросание монетки на крайний случай, зачем вам новые долги?)

Для четверки еще всего лишь неправильно вторую останется порешать)»

ДАНО:

0) ПС: не обязательно, это для удобства дальше пригодится.
Пронумеруйте строчки задания слева цифрами в кружочке. Это будут их порядковые номера, чтобы потом не запутаться. (Их будете писать потом у самих линий и считая точки.)

1) Просто перепишите второй раз все строчки, изменив знаки "больше либо равно" и "меньше либо равно" на просто "равно".

1,5) Пс: Не обязательно. Можно переписать все функции, выразив, чему равно «Х1», чтобы потом легче считать, но можно и не делать так, а сразу считать, как удобнее.

2) Теперь строим график. Начертите оси (горизонтальная "Х1", вертикальная "Х2"), одной клеточке равно одно деление.
Обязательно отметьте пересечение "0", чтобы после не сбиться в линиях и отсчетах.
ПС: Лучше чертить идеально ровно, а не произвольно! В конце это позволит вам просто увидеть верные координаты точки на плоскости, если по формуле не сможете.

3) Теперь чертим линии. Каждая строчка это отдельная функция, которая на графике будет прямой линией.

Одна из строчек задания у всех: "Х1, Х2 >= 0".
Это сами оси координат, их нужно учитывать позже.

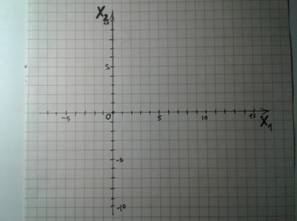
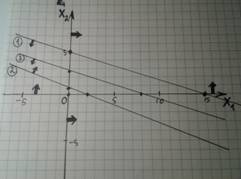
Чертим линии: сначала считаем координаты двух точек, которые после соединяем в линию. (Для удобства можно не переписывать саму функцию, а поставить порядковый номер, который вначале давали).

Как найти эти две точки:
Нужно подставить в формулы любые значения для "Х1", а потом для "Х2". (Не обязательно, но намного удобнее взять в обоих случаях "0"!!!!

Так Вы сразу будете видеть точные пересечения с осями, и в дальнейшем увидите верный ответ и по картинке.)
Сначала подставляем в первую формулу "Х1" = 0, вычисляем только по первой формуле, подставляем и находим "Х2". Сразу эту точку отмечаем на плоскости, чтобы не запутаться.
Потом считаем вторую точку для этой прямой: подставляем а эту же первую формулу "Х2" = 0, находим из формулы "Х1". Сразу рисуем эту точку на плоскости.

Соединяем полученные две точки, получилась построенная первая функция.
Обязательно подписываем ее сбоку порядковым номером "1" (или переписываем саму формулу), позже понадобится знать, где какая функция!

Делаем тоже самое для всех строчек задания!!!
Обязательно подписывайте все линии или обозначайте порядковыми номерами!!!

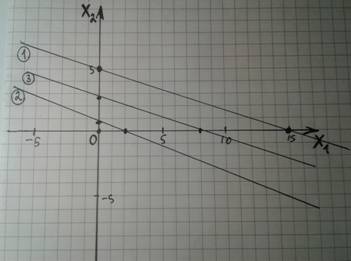
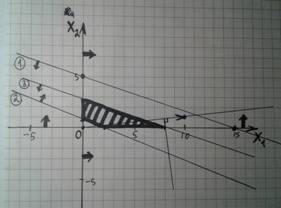
4) Теперь ставим стрелочки у линий, чтобы понять, с какой стороны она верна.

(Это ОДЗ для каждой функции).
Для этого нужно взять координаты любой точки, (не лежащей на самой прямой, а находящейся на пустом месте на графике), и подставить в первоначальную функцию (которые со знаками ">=" и "<=").
Для облегчения жизни всегда берите точку 0!!! Она по обоим осям "= 0". (Но если линия проходит через эту точку 0, то надо взять любую другую точку, не лежащую на прямой линии!) (Берите нули, легче в уме считать).

К примеру: к первой формуле подставляем вместо "Х1" и "Х2" нули, и проверяем верно ли утверждение, что между левым значением и правым верный ли знак теперь получается, если "да", то рисуем стрелку от линии с номером "1" в сторону данной точки (в нашем случае к нулю), если утверждение получилось неверное, то рисуем стрелку от линии в сторону от нуля!!!
Повторяем для каждой строчки!!!

Одна из строчек у всех "Х1, Х2 >= 0", это оси координат, от них ставим стрелки в первую четверть графика (от нуля вправо вверх получается, в той четверти графика), (то есть от вертикальной оси стрелку вправо, от горизонтальной вверх), (пс: короче, в положительных числах графика, это по логике, что, допустим цены и количество продукции не могут быть отрицательными. И это же самое правило в конце для проверки используем!!! Наш ответ выделенной фигуры может быть исключительно в этой части графика (=в первой четверти).

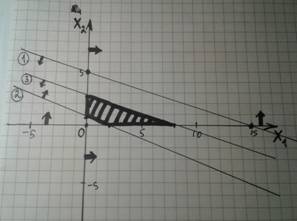
5) Теперь находим ОДЗ (=область допустимых значений). = Оно же полученный многоугольник пересечения областей.
Как делаем: (несколько вариантов) обводим ту область пересечения, которая относится ко всем стрелкам, если не видите ее сразу, то лучше проверьте отдельно, как обведете, проверьте еще раз, попадает ли вся данная область под все стрелки, возможно, какой-то кусок лишний или не всю выделили. Это повлияет дальше на ответ, поэтому надо верно выбрать!!! Выбранную фигуру обведите и заштрихуйте, чтобы было четко видно.

Второй вариант: можно разными линиями (к примеру, пунктирной, с точками, волнистой, крестиками..., главное для каждой линии свое обозначение), заштриховать области каждой линии, и пересечение всех областей общих обвести фигурой.
В обоих случаях получится одинаковая фигура!

Важно: проверьте, чтобы полученная область была в первой четверти графика (от нуля направо вверх).
Исключение: если в данных задачи, случайно, не оказалось строчки "Х1, Х2 >= 0".

Тогда область может быть в любом месте пересечения, тогда оси не воспринимаем линиями.)

6) Теперь строим градиент.

Из данных задачи из формулы «С(Х)» берем цифры перед «Х1» и «Х2» со знаками перед ними, не обращая внимания на просто число (если оно есть) без иксов. Эти две цифры будут нашей точкой по данным осям.

Отмечаем точку на графике очень заметно.

Рисуем прямую между этой точкой и 0 (пересечение координат).

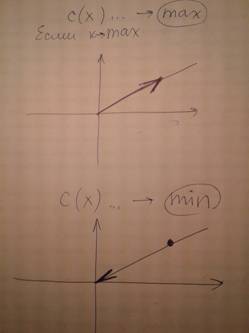
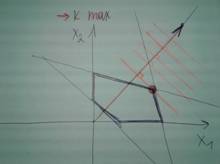
7) Рисуем направление стрелки градиента.

Если в формуле «С(Х)» в конце стоит «стремится к MAX», то рисуем стрелку от нуля в сторону точки.

Если в формуле «С(Х)» в конце стоит «стремится к MIN», то рисуем стрелку от точки в сторону нуля.

На рисунках ниже различные варианты для разных случаев (не забудьте о знаке перед цифрой, его тоже нужно учитывать для точки, на рисунке видно как стрелку указывать если С(Х) стремится к минимуму или к максимуму:

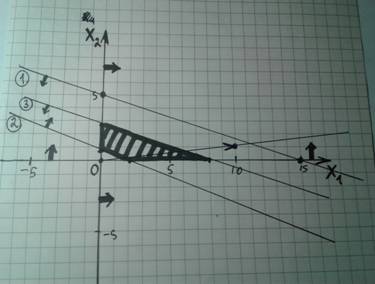
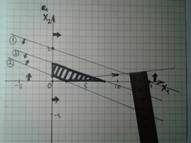
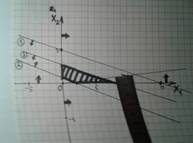
8) Теперь рисуем перпендикуляр (это 90 градусов к линии) к вектору (градиенту). Можно просто приложить линейку или просто лист к вектору. Нужно начинать вести перпендикуляры со стороны стрелки!!! (ПС: Если фигура больше намного, то надо начинать вести его первоначально дальше, и доходя до фигуры.) 

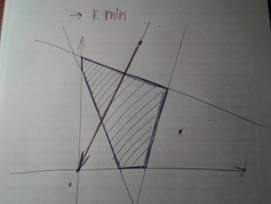
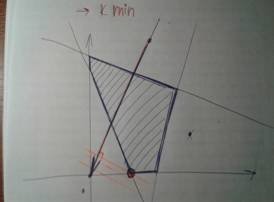
В итоге надо найти самую крайнюю точку в фигуре, которая ближе всего к той стороне вектора, где стрелка (Самая крайняя точка с той стороны).

На рисунках ниже различные примеры перпендикуляров для максимума и для минимума.

9) Когда нашли точку, то смотрим по графику какими прямыми она образуется. Для удобства мы их в начале пронумеровали.

Теперь выписываем ДВЕ функции из самого начала задания под этими номерами. (Так как точка образуется на стыке двух линий)

(ПС: если в итоге вышла не точка, а целая линия, а так может быть, то плохо, я ничем не могу помочь, не знаю как решить эту проблему)) Интересно дочитали ли вы до сюда))

В итоге получили систему из двух функций, слева от них поставьте скобочку как в самом начале была.

10) Теперь из этих двух функций найдите «Х1» и «Х2». Сначала из одной выразите «Х1», из которой проще, потом это выражение, чему равно, подставьте во вторую функцию.

 В итоге вышла координата точки.

(Можете проверить по рисунку, она должна совпасть с выделенной в итоге точкой.)

Если не получилось по формуле найти эту точку, то выпишите ее по координатам с рисунка)) Сначала по оси «Х1», потом «Х2», и это в скобочки круглые. Пример: (5;8).

Это получилось оптимальное решение.

11) Теперь подставляем эти координаты точки в формулу С(Х), получится число, это ответ на задачу.

«Вы большие молодцы! Справились с такой сложной задачей самостоятельно!)))

Если не получилось, проверьте сначала сами снова по плану, может чего-то пропустили) хотя бы дойдите до построения градиента) и обращайтесь)» =)*