
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Перекачка предварительно подогретых нефтей и нефтепродуктов
Рассмотрим движение вязкой парафинистой нефти по трубопроводу при неизотермическом установившемся режиме. Полагаем, что, если парафин кристаллизируется, то он уносится потоком, не оседая на стенках трубы. В общем случае уравнение теплового баланса для элемента трубопровода длиной dx .отстоявшего на расстоянии x , будет Первое слагаемое-это потери в окружающую среду с элемента трубопровода длиной dx (k - коэффициент теплопередачи; D - внутренний диаметр трубопровода; Т - температура нефти в трубопроводе на расстоянии X от начала; Т0 - температура окружающей среды (грунта), постоянная, осредненная по длине). Второе слагаемое представляет собой теплоту трения в рассматриваемом сечения (Q - объемный расход нефти ρ - плотность нефти, i - гидравлический уклон). Так как теплота трения частично компенсирует теплопотери, то перед вторым слагаемым поставлен знак минус. Третье слагаемое - это тепло, выделяющееся при кристаллизации парафина (ε - массовое содержание парафина в нефти (в долях); χ - теплота кристаллизации; Тнп и Ткп - соответственно температура начала и конца выпадения парафина). Тепло кристаллизации также частично компенсирует теплопотери в окружающую среду. Но, имея ввиду, что dT отрицательное (температура по длине падает), то знак перед третьим слагаемым будет плюс (минус на минус дает плюс). В правой части уравнения теплового баланса записано изменение теплосодержания (Ср - теплоемкость нефти). Так как градиент отрицательный, то принят знак минус. Приняв среднее значение гидравлического уклона, разделяя переменные, интегрируя и имея в виду, что при X = 0, Т=Тн, получим  или где Если парафин отсутствует, то положив ε=0, из (2) и (3) получим формулу Лейбензона. Если к тому же нефть маловязкая, то можно пренебречь теплотой трения (b= 0) и из (2) и (3) получим формулу Шухова. Для маловязкой, но парафинистой нефти в формуле (3) следует положить b=0. Характер изменения температуры по длине трубопровода для различных нефтей показан на рис.1. Видим, что самые высокие темпы снижения температуры присущи формуле Шухова. Тепло трения и теплота кристаллизации снижают интенсивность охлаждения жидкости в трубопроводе. Расчет теплового режима магистрального трубопровода является трудоемким, так как в общем случае могут быть участки, где парафин не выпадает (Тн>Тнп и Т>Ткп) и где он выпадает (Тнп≥Т≥Ткп). В области высоких температур можно не учитывать теплоту трения, а при низких температурах она составляет значимую долю в тепловом балансе. Кроме этого, в трубопроводе могут быть два режима течения: на начальном участке, где температуры высокие, возможен турбулентный режим течения, а на оставшейся длине - ламинарный. Трудность расчета заключается в согласовании условий на границах различных участков. Для упрощения изложения будем рассматривать случай наиболее интенсивного охлаждения, т.е. температура по длине трубопровода выражается формулой Шухова, которая получается из (7.8) при b=0, ε=0;
Рис. 1. Изменение температуры нефти по длине трубопровода: 1 – по формуле Шухова, С*p=Ср , b=0; 2 – по формуле Лейбензона, ε=0; 3 – по формуле (7.9), С*p>Ср ,ε≠0 , b≠0; 4 – по формуле (7.9), С*p>Ср ,ε≠0 , b=0
Рис. 2. Течение нефти в трубопроводе при двух режимах
Применяя ее к турбулентному участку, надо положить К=Кт: (см. рис. 2). В конце турбулентного участка температура где В конце трубопроводного участка температура
или
По аналогии для ламинарного участка можно записать (при К = Кл) где В конце ламинарного участка температура или
На основании (6) и (8), исключая LТ, можно получить соотношение, связывающее все граничные температуры в трубопроводе с двумя режимами течения: Критическую температуру Ткр, соответствующую переходу турбулентного режима в ламинарный (и наоборот), определяют следующим образом. Исходя из критического значения параметра Re≈2000, находим соответствующий ему коэффициент кинематической вязкости Затем по вискограмме для данной нефти находим Ткр. Ее можно найти и аналитически. Например, подставив в формулу (1) νкр и Ткр и решая совместно с (9), найдем Используя другие аналитические зависимости для вязкости, можно найти соответствующие им формулы для Ткр. Коэффициент теплопередачи для трубопроводов зависит от внутреннего α1 и внешнего α2 коэффициентов тсплоотдатчи, а также от термического сопротивления стенки трубы, изоляции, отложений и т.п. где D - внутренний диаметр трубопровода; n - число слоев, учитываемых в термическом сопротивлении при расчете; λi коэффициенты теплопроводности слоев (отложений, стали трубы, изоляции и т.п.); Di, Dнi - соответственно внутренний и наружный диаметры каждого слоя; Dн - наружный диаметр трубопровода (диаметр поверхности, соприкасающейся с грунтом). Для определения α1 при вынужденном движении жидкости имеются различные экспериментальные зависимости. Теплофизические характеристики в приведенных зависимостях определяются при средних температурах потока и стенки трубы (индекс «СТ»), а за определяющий размер принят внутренний диаметр трубы. Теплофизические характеристики рассчитываются по формулам Крего. В переходной области внутренний коэффициент теплоотдачи α1, можно определять приближенно интерполяцией. Для внешнего коэффициента теплоотдачи α2 подземного трубопровода используют формулу Форхгеймера-Власова где λГ - коэффициент теплопроводности грунта; Н - глубина заложения трубопровода в грунт (до оси). При 2Н/Дн > 2 (с погрешностью до 1 %) При малых заглублениях (H/Dн<3-4) пользуются формулой Аронса-Кутателадзе
|
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 309. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . (1)
. (1) , (2)
, (2) , (3)
, (3) ;
;  ;
; 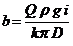 .
. , (4)
, (4)

 , (5)
, (5) ; 0 ≤ X ≤ L; Tн ≥ T ≥ Tкр (см. рис. 7.2)
; 0 ≤ X ≤ L; Tн ≥ T ≥ Tкр (см. рис. 7.2) , (6)
, (6)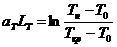 .
.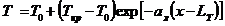 , (7)
, (7) ; LТ ≤ x ≤ L; Tкр ≥ T ≥ Tк
; LТ ≤ x ≤ L; Tкр ≥ T ≥ Tк , (8)
, (8) .
. . (9)
. (9) . (10)
. (10) , (11)
, (11) , (12)
, (12) . (13)
. (13) , (14)
, (14)