
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Реализация очереди с приоритетами частично упорядоченными деревьямиСтр 1 из 3Следующая ⇒ Очереди с приоритетами. Методы их реализации Термин "очередь с приоритетами" подразумевает, что на множестве элементов задана функция приоритета (priority), т.е. для каждого элемента а множества можно вычислить функцию р(а), приоритет элемента а, которая обычно принимает значения из множества действительных чисел, или, в более общем случае, из некоторого линейно упорядоченного множества. Очередь с приоритетами, которая возникает среди множества процессов, ожидающих обслуживания совместно используемыми ресурсами компьютерной системы. Обычно стараются сделать так, чтобы короткие процессы выполнялись незамедлительно (на практике "незамедлительно" может означать одну-две секунды), т.е. такие процессы получают более высокие приоритеты, чем процессы, которые требуют (или уже израсходовали) значительного количества системного времени. Процессы, которые требуют нескольких секунд машинного времени, не выполняются сразу - рациональная стратегия разделения ресурсов откладывает их до тех пор, пока не будут выполнены короткие процессы. Однако нельзя переусердствовать в применении этой стратегии, иначе процессы, требующие значительно больше времени, чем "средние" процессы, вообще никогда не смогут получить кванта машинного времени и будут находиться в режиме ожидания вечно. Один возможный путь удовлетворить короткие процессы и не заблокировать большие состоит в задании процессу Р приоритета, который вычисляется по формуле 100tисп(P) - tнач(P), где параметр tисп(P) равен времени, израсходованному процессом Р ранее, а tнач(P) - время, прошедшее от начала инициализации процесса, отсчитываемое от некоего "нулевого времени". В общем случае приоритеты будут большими отрицательными целыми числами, если, конечно, tнач(P) не отсчитывается от "нулевого времени" в будущем. Число 100 в приведенной формуле пришло из практики и не поддается четкому логическому обоснованию; оно должно быть несколько больше числа ожидаемых активных процессов. Легко увидеть, что если всегда сначала выполняется процесс с наименьшим приоритетным числом и если в очереди немного коротких процессов, то в течение некоторого (достаточно продолжительного) времени процессу, который не закончился за один квант машинного времени, будет выделено не менее 1% машинного времени. Если этот процент надо увеличить или уменьшить, следует заменить константу 100 в формуле вычисления приоритета.  Реализация очередей с приоритетами. За исключением хеш-таблиц, те реализации множеств, которые рассмотрены ранее, можно применить к очередям с приоритетами. Хеш-таблицы следует исключить, поскольку они не имеют подходящего механизма нахождения минимального элемента. Т.е., применение хеширования привносит дополнительные сложности, которых лишены, например, связанные списки. При использовании связанных списков можно выбрать вид упорядочивания элементов списка или оставить его несортированным. Если список отсортирован, то нахождение минимального элемента просто - это первый элемент списка. Но вместе с тем вставка нового элемента в отсортированный список требует просмотра в среднем половины элементов списка. Если оставить список неупорядоченным, упрощается вставка нового элемента и затрудняется поиск минимального элемента. Исходя из того, что рассматриваемые нами деревья являются двоичными, по возможности сбалансированными и на самом нижнем уровне все листья "сдвинуты" влево, можно применить для этих деревьев необычное представление, которое называется куча. В этом представлении используется массив, назовем его А, в котором первые n позиций соответствуют n узлам дерева. А[1] содержит корень дерева. Левый сын узла A[i], если он существует, находится в ячейке A[2i], а правый сын, если он также существует, - в ячейке A[2i+1]. Обратное преобразование: если сын находится в ячейке A[i], i>1, то его родитель - в ячейке A[i div 2]. Отсюда видно, что узлы дерева заполняют ячейки А[1], А[2], ..., A[n] последовательно уровень за уровнем, начиная с корня, а внутри уровня - слева направо.
Реализация очереди с приоритетами частично упорядоченными деревьями Для представления очередей с приоритетами посредством списков требуется затратить время, пропорциональное n для выполнения операторов INSERT и DELETEMIN на множестве размера n. Существует другая реализация очередей с приоритетами, в которой на выполнение этих операторов требуется порядка O(log n) шагов. Основная идея такой реализации заключается в том, чтобы организовать элементы очереди в виде сбалансированного (по возможности) двоичного дерева. Сбалансированность в данном случае конструктивно можно определить так: листья возможны только на самом нижнем уровне или на предыдущем, но не на более высоких уровнях.
Наш элемент надо спустить еще на более низкий уровень, так как его сыновья сейчас имеют приоритеты б и 8. Меняем его местами с сыном, имеющим наименьший приоритет 6. Получено в результате такого обмена новое дерево:
Таким образом, описанный процесс спуска элемента по дереву приводит к частичному упорядочиванию двоичного дерева.
33. Деревья двоичного поиска Деревья двоичного поиска - основная структура данных для представления множеств, чьи элементы упорядочены посредством некоторого отношения линейного порядка, которые, как обычно, обозначим символом "<". Эти структуры особенно полезны, когда исходное множество такое большое, что не рационально использовать его элементы непосредственно в качестве индексов массивов. Предполагается, что все элементы множеств являются элементами некоторого универсального множества - универсума, примером которого служит множество возможных идентификаторов в программе на языке Pascal.
Это свойство называется характеристическим свойством дерева двоичного поиска и выполняется для любого узла дерева двоичного поиска, включая его корень. На рисунке показаны два дерева двоичного поиска, представляющие одно и то же множество целых чисел Отметим интересное свойство деревьев двоичного поиска: если составить список узлов этого дерева, обходя его во внутреннем (симметричном) порядке, то полученный список будет отсортирован в порядке возрастания (в соответствии с заданным на множестве отношением линейного порядка).
34. Нагруженные деревья Рассмотрим специальную структуру для представления множеств, состоящих из символьных строк. Некоторые из описанных здесь методов могут работать и со строками объектов другого типа, например со строками целых чисел. Эта структура данных называется нагруженными деревьями (tries). В оригинале структура называется trie, это слово получено из букв, стоящих в середине слова "retrieval" (поиск, выборка, возврат). Устоявшегося термина для этой структуры в русской литературе пока нет. О расхождении терминологии можно судить по следующему факту: 1) в известной книге Кнут Д. Искусство программирования для ЭВМ. Т.3: Сортировка и поиск. - М.,Мир, 1978г. вместо trie используется термин бор (от слова выборка), 2) а в последнем переводе переработанного издания этой книги (Кнут Д. Искусство программирования. Т.3: Сортировка и поиск. - М., Вильямс, 2000г.) - термин луч (от слова получение).Термин нагруженные деревья соответствует смыслу этой структуры. Можно было бы применить и термин синтаксические деревья, но, хотя этот термин по своему значению и "пересекается" с термином нагруженные деревья, он имеет другую направленность. Структура нагруженных деревьев поддерживает операторы множеств, у которых элементы являются словами, т.е. символьными строками. Удобно, когда большинство слов начинается с одной и той же последовательности букв или, другими словами, когда количество различных префиксов значительно меньше общей длины всех слов множества. В нагруженном дереве каждый путь от корня к листу соответствует одному слову из множества. При таком подходе узлы дерева соответствуют префиксам слов множества. Чтобы избежать коллизий слов, подобных THE и THEN, введем специальный символ $, маркер конца, указывающий окончание любого слова. Тогда только слова будут словами, но не префиксы. Самой простой реализацией узлов нагруженного дерева будет массив node указателей на узлы с индексным множеством {А, В, ..., Z, $}. Так как мы рассматриваем каждый узел нагруженного дерева как отображение, то можно применить любую реализацию отображений. Но при условии подбора отображений со сравнительно малой областью определения, наилучшим выбором будет реализация отображения посредством связанных списков.
35. Реализация множеств посредством сбалансированных деревьев Подробно рассмотрим одну из таких реализаций, которая называется 2-3 дерево и имеет следующие свойства. 1) Каждый внутренний узел имеет или два, или три сына. 2) Все пути от корня до любого листа имеют одинаковую длину. Будем считать, что пустое дерево и дерево с одним узлом также являются 2-3 деревьями. Рассмотрим представления множеств, элементы которых упорядочены посредством некоторого отношения линейного порядка, обозначаемого символом "<". Элементы множества располагаются в листьях дерева, при этом, если элемент а располагается левее элемента b, справедливо отношение а < b. Предполагаем, что упорядочивание элементов по используемому отношению линейного порядка основывается только на значениях одного поля (среди других полей записи, содержащей информацию об элементе), которое формирует тип элементов. Это поле назовем ключом. Например, если элементы множества - работники некоторого предприятия, то ключевым полем может быть поле, содержащее табельный номер или номер карточки социального страхования. В каждый внутренний узел записываются ключ наименьшего элемента, являющегося потомком второго сына, и ключ наименьшего элемента – потомка третьего сына, если, конечно, есть третий сын. Отметим, что 2-3 дерево с k уровнями имеет от 2k-1 до Зk-1листьев. Другими словами, 2-3 дерево, представляющее множество из n элементов, будет иметь не менее 1+log3n и не более 1+log2n уровней. Таким образом, длины всех путей будут иметь порядок O(logn). Можно найти запись с ключом х в множестве, представленном 2-3 деревом, за время O(logn) путем простого перемещения по дереву, руководствуясь при этом значениями элементов, записанных во внутренних узлах. Во внутреннем узле node ключ х сравнивается со значением у наименьшего элемента, являющегося потомком второго сына узла node. · Если х<у, то перемещаемся к первому сыну узла node. · Если х³у и узел node имеет только двух сыновей, то переходим ко второму сыну узла node. · Если узел node имеет трех сыновей и х³у, то сравниваем х со значением z - вторым значением, записанным в узле node, т.е. со значением наименьшего элемента, являющегося потомком третьего сына узла node: o если х<z, то переходим ко второму сыну, o если х³z, переходим к третьему сыну узла node. · Таким способом в конце концов мы придем к листу, и элемент х будет принадлежать исходному множеству тогда и только тогда, когда он совпадает с элементом, записанным в листе. Очевидно, что если в процессе поиска получим х=у или х=z, поиск можно остановить. Но, конечно, алгоритм поиска должен предусмотреть спуск до самого листа. Процесс вставки нового элементах в 2-3 дерево начинается так же, как и процесс поиска элемента х. · Пусть мы уже находимся на уровне, предшествующем листьям, в узле node, чьи сыновья (уже проверено) не содержат элемента х. · ü Ограничимся представлением посредством 2-3 деревьев множеств элементов, чьи ключи являются действительными числами. Общий тип записи обозначим как elementtype. ü При написании программ на языке Pascal родители листьев должны быть записями, содержащими два поля действительных чисел (ключи наименьших элементов во втором и в третьем поддеревьях) и три поля указателей на элементы. ü Родители этих узлов являются записями, состоящими из двух полей действительных чисел и трех полей указателей на родителей листьев. ü Таким образом, разные уровни 2-3 дерева имеют разные типы данных (указатели на элементы или указатели на узлы). ü Эта ситуация вызывает затруднения при программировании на языке Pascal операторов, выполняемых над 2-3 деревьями. Но язык Pascal имеет механизм, вариант структуры record (запись), который позволяет обращаться с узлами 2-3 дерева, имеющими разный тип данных. В данном случае все равно каждый узел будет занимать пространство, равное пространству, занимаемому самым "большим" типом данных. Поэтому язык Pascal - не лучший язык для практической реализации 2-3 деревьев.
36. Множества с операторами MERGE и FIND Рассмотрим ситуацию, когда есть совокупность объектов, каждый из которых является множеством. Основные действия, выполняемые над такой совокупностью, заключаются в объединении множеств в определенном порядке, а также в проверке принадлежности определенного объекта конкретному множеству. Эти задачи решаются с помощью операторов MERGE (Слить) и FIND (Найти). · Оператор MERGE(A, В, С) делает множество С равным объединению множеств А и В, если эти множества не пересекаются (т.е. не имеют общих элементов); этот оператор не определен, если множества А и В пересекаются. · Функция FIND(x) возвращает множество, которому принадлежит элемент х; в случае, когда х принадлежит нескольким множествам или не принадлежит ни одному, значение этой функции не определено. Пример. Отношением эквивалентности является отношение со свойствами рефлексивности, симметричности и транзитивности. Другими словами, если на множестве S определено отношение эквивалентности, обозначаемое символом "º", то для любых элементов а, b и с из множества S (не обязательно различных) справедливы следующие соотношения. 1) а º а (свойство рефлексивности). 2) Если а º b, то b º а (свойство симметричности). 3) Если а º b и b º с, то а º с (свойство транзитивности). Отношение равенства (обозначается знаком "=") - это пример отношения эквивалентности на любом множестве S. Для любых элементов а, b и с из множества S имеем 1) а = а; 2) если а = b, то b= а; 3) если а = b и b= с, то а = с. В общем случае отношение эквивалентности позволяет разбить совокупность объектов на непересекающиеся группы, когда элементы а и b будут принадлежать одной группе тогда и только тогда, когда а = b. Если применить отношение равенства (частный случай отношения эквивалентности), то получим группы, состоящие из одного элемента. Более формально можно сказать так: · если на множестве S определено отношение эквивалентности, то в соответствии с этим отношением множество S можно разбить на непересекающиеся подмножества S1, S2, ..., которые называются классами эквивалентности, и объединение этих классов совпадает с S. · Таким образом, а ºb для всех а и b из подмножества Si, но а не эквивалентно b, если они принадлежат разным подмножествам. Например, отношение сравнения по модулюn - это отношение эквивалентности на множестве целых чисел: · а-а=0 (рефлексивность), · если а-b=dn, то b-а=(-d)n (симметричность), · если а-b=dn и b-c=en, то а-с=(d+е)n (транзитивность). Существует n классов эквивалентности, каждое из которых является множеством целых чисел: · первое множество состоит из целых чисел, которые при делении на n дают остаток 0, · второе множество состоит из целых чисел, которые при делении на n дают остаток 1 · и т.д., · n-е множество состоит из целых чисел, которые дают остаток n-1. Методы реализации. Предположим, что мы объявили тип MFSET как массив components (компоненты), предполагая, что components[x] содержит имя множества, которому принадлежит элемент х. При этих предположениях операторы АТД MFSET реализуются легко, что видно из листинга 6.13 с кодом процедуры MERGE. Процедура INITIAL(A, x) просто присваивает components[x] значение А, а функция FIND(x) возвращает значение components[x]. Время выполнения операторов при такой реализации MFSET легко проанализировать: · время выполнения процедуры MERGE имеет порядок О(n), · а для INITIAL и FIND время выполнения фиксированно, т.е. не зависит от n. Применение алгоритма из листинга 6.13 для последовательного выполнения n-1 раз оператора MERGE займет время порядка O(n2). Один из способов ускорения выполнения оператора MERGE заключается в связывании всех элементов компонента в отдельные списки компонентов. Тогда при слиянии компонента В в компонент А вместо просмотра всех элементов необходимо будет просмотреть только список элементов компонента В. Такое расположение элементов сократит среднее время слияния компонентов. Другой подход к реализации АТД MFSET применяет деревья с указателями на родителей. Опишем этот подход неформально. Основная идея здесь заключается в том, что узлы деревьев соответствуют элементам множеств и есть реализация, посредством массивов или какая-либо другая, отображения множества элементов в эти узлы.
37. Задача наибольшей общей подпоследовательности Подпоследовательность последовательности х получается в результате удаления нескольких элементов (не обязательно соседних) из последовательности х. Имея две последовательности х и у, наибольшая общая подпоследовательность (НОП) определяется как самая длинная последовательность, являющаяся подпоследовательностью как х, так и у. Например, для последовательностей НОП составляет подпоследовательность 2, 3, 2, 1. В этом примере существуют и другие НОП, в частности 2, 3, 1, 2, но нет ни одной общей подпоследовательности длиной 5. Существует команда UNIX diff, которая, сравнивая файлы строка за строкой, находит наибольшую общую подпоследовательность, при этом рассматривая каждую строку файла как отдельный элемент подпоследовательности (т.е. здесь целая строка является аналогом целых чисел из примера). После выполнения команды diff строки, не вошедшие в НОП, могут быть удалены, изменены или перемещены из одного файла в другой. Например, если оба файла являются версиями одной и той же программы, выполненными с разницей в несколько дней, то оператор diff, скорее всего, найдет расхождения в этих версиях. Существуют различные способы решения задачи НОП, которые требуют выполнения порядка О(n2) шагов для последовательностей длиной n. Команда diff использует дифференцированную стратегию, которая работает хорошо, если файлы не имеют слишком больших повторений в строках. Например, в программах обычно много повторяющихся строк "begin" и "end", но другие строки не должны повторяться также часто. Алгоритм, использующий команду diff для поиска НОП, можно применить в эффективной реализации множеств с операторами MERGE и SPLIT. В этом случае время выполнения алгоритма поиска НОП составит О(р logn), где n - максимальное число строк в файле, а р - число пар позиций с совпадающими строками, когда одна позиция из одного файла, а другая из другого. Например, для последовательностей из примера слайда 116 число р равно 12. Две единицы в каждой последовательности образуют 4 пары, три двойки в верхней последовательности и две в нижней дадут 6 пар, а тройки и четверки - еще 2 пары. В самом худшем случае р может иметь порядок n2, тогда алгоритм поиска НОП будет выполняться за время О(n2logn). На практике р обычно близко к n, поэтому можно ожидать время выполнения порядка О(nlogn). Перед началом описания алгоритма предположим, что есть две строки (последовательности) элементов А=a1a2...an и В=b1b2...bm, для которых ищется НОП. Первым шагом алгоритма будет составление для каждого элемента а списка позиций строки A, на которых стоит этот элемент. Таким способом определяется множество PLACES(a) = { i | a=ai }. Для вычисления множеств PLACES(a) можно создать отображение из множества элементов в заголовки списков позиций. При использовании хеш-таблиц можно вычислить множества PLACES(a) в среднем за О(n) "шагов", где "шаг" - это действия, выполняемые при обработке одного элемента. Время, затрачиваемое на выполнение одного "шага", будет константой, если элемент, например, является символом или числом. Но если элементы в последовательностях А и В являются текстовыми строками, то время выполнения "шага" будет зависеть от средней длины текстовых строк.Имея построенные множества PLACES(a) для каждого элемента а последовательности А, можно приступать к нахождению НОП. Упрощая изложение материала, мы покажем только, как определить длину НОП. Алгоритм будет по очереди просматривать все bj, где j=1, 2, ..., m. После обработки очередного bj мы должны для каждого i от 0 до n знать длину НОП для последовательностей a1, ..., ai и b1,..., bj. Значения позиций группируются в множества Sk (k=0, 1, ..., n), состоящие из всех целых чисел (позиций) i таких, что существует НОП длины k для последовательностей a1, ..., ai и b1,..., bj. Отметим, Sk всегда являются множествами последовательных целых чисел и для любого k числа в Sk+1 больше, чем в Sk.
38. Сбалансированные и несбалансированные деревья поиска Дерево называется идеально сбалансированным, если все его уровни, за исключением, может быть, последнего, полностью заполнены. В бинарном дереве полностью заполненный уровень n содержит 2n узлов. Если дерево поиска близко к сбалансированному, то даже в худшем случае за время порядка O(log2n) в нем можно: · Найти вершину с заданным значением или выяснить, что такой вершины нет. · Включить новую вершину. · Исключить вершину.
В этом дереве 7 узлов, на последнем уровне находится 4 узла. Если доступ к одному узлу требует 1 единицу времени, то до узла 4 можно добраться за 1 единицу времени, до 2 и 6 - за 2, до 1, 3, 5, 7 - за 3. То есть в худшем случае требуется 3 единицы времени, в среднем: (1+2*2+3*4)/7 = 2.4 единицы времени. Однако значения в последовательности могут идти и в другом порядке, что может привести к построению несбалансированного дерева. В худшем случае можно получить вырожденное дерево, подобное линейному списку. То есть для вырожденного дерева затраты на доступ к узлам в худшем случае имеют порядок O(n), в среднем - O(n/2). при работе с деревьями поиска больших размеров крайне желательно, чтобы они были близки к сбалансированным.Приведение уже существующего дерева к идеально сбалансированному - процесс сложный. Проще балансировать дерево в процессе его роста, т.е. после включения каждого узла. Однако требование идеальной сбалансированности делает и этот процесс достаточно сложным, способным затрагивать все узлы дерева.
39. АВЛ-деревья В 1962 году советские математики Г.М.Адельсон-Вельский и Е.А.Ландис предложили метод балансировки, требующий после включения или исключения узла лишь локальные изменения вдоль пути от корня к данному узлу, то есть времени не более O(log2n). При этом деревьям разрешается отклоняться от идеальной сбалансированности, но в небольшой степени, чтобы среднее время доступа к узлам было лишь немногим больше, чем в идеально сбалансированном дереве. Такие деревья называются АВЛ-деревьями. Критерий сбалансированности АВЛ-дерева. Дерево называется сбалансированным тогда и только тогда, когда для каждого его узла высоты его левого и правого поддеревьев отличаются не более чем на единицу. Примеры АВЛ-сбалансированных деревьев:
Уровень 1 сбалансированности как разность между высотой правого и Уровень 2 левого поддерева данного узла. Пусть hR - высота правого Уровень 3 поддерева, hL - высота левого. Тогда показатель сбалансированности есть hR - hL.Если дерево АВЛ-сбалансировано, то для каждого узла выполняется: |hR - hL| £1. Если хотя бы для одного узла дерева это не так, то дерево не является АВЛ-сбалансированным. После включения нового узла в АВЛ-дерево оно должно оставаться сбалансированным. Рассмотрим, в каких случаях потребуется балансировка дерева после включения узла. Во всех случаях будем указывать показатель сбалансированности корневого узла. Балансировка выполняется с помощью действий, называемых поворотами узлов. Одинарный LL-поворот. Выполняется, когда «перевес» идет по пути L-L Одинарный RR-поворот.
.
Одинарный LR-поворот. Выполняется, когда «перевес» идет по пути L-R от узла с нарушенной балансировкой.
Правило балансировки: При включении узлов повороты выполняются для ближайшего узла к включенному с нарушенной балансировкой. То есть если после включения узла в дереве образуется несколько узлов с нарушенной балансировкой, поворот выполняется для того, который находится ниже (то есть ближе к включенному). После балансировки этого узла восстанавливается баланс и выше расположенных узлов. Ясно, что включение узла в АВЛ-дерево в среднем требует больше времени, чем включение в обычное дерево, так как может возникать необходимость проведения балансировки. Поэтому АВЛ-деревья целесообразно использовать в тех случаях, когда поиск узлов в дереве происходит гораздо чаще, чем включение и исключение улов.
40. Для представления графов можно использовать различные структуры данных. Выбор структуры данных зависит от операторов, которые будут применяться к вершинам и ребрам графа. Представления графов матрицей смежности. Одним из наиболее общих представлений графа G = (V, Е) является матрица смежности. Пусть G=(V, E), где V={v1, v2, …, vn}.Матрица смежности для графа G - это матрица А размера nхn со значениями булевого типа, где A[i, j] = true тогда и только тогда, когда существует ребро из вершины i в вершину j. Часто в матрицах смежности значение true заменяется на 1, а значение false - на 0. Время доступа к элементам матрицы смежности зависит от размеров множества вершин и множества ребер. Представление графа в виде матрицы смежности удобно применять в тех алгоритмах, в которых надо часто обрабатывать ребра между парами вершин.Для представления неориентированных графов можно применять матрицу смежности, если неориентированное ребро между вершинами v и w рассматривать как две ориентированных дуги от вершины v к вершине w и от вершины w к вершине v. Очевидно, что матрица смежности для неориентированного графа симметрична. Представления графов матрицей инциденций.Если количество ребер или дуг графа значительно меньше количества вершин, то эффективно представлять графы матрицами инциденций. Пусть G=(V, E), где V={v1, v2, …, vn}, E={e1, e2, …, em}.Матрица инциденций для графа G - это матрица B размера nхm со значениями булевого типа, где B[i, j] = true тогда и только тогда, когда ребро из вершины i инцидентно ребру j. Часто в матрицах инциденций значение true заменяется на 1, а значение false - на 0. В каждом столбце матрицы инциденций всегда ровно две единицы, остальные элементы равны нулю. Если в графе все вершины имеют степень ноль, то матрицы инциденций не существует. Время доступа к элементам матрицы инциденций зависит от размеров множества вершин и множества дуг. Представление графа в виде матрицы инциденций удобно применять в тех алгоритмах, в которых надо часто обрабатывать ребра между парами вершин для построения путей, обхода ребер и т.п..Представления графов списками смежности.Вместо матриц смежности или инциденций часто используется другое представление для графа G = (V, Е), называемое представлением посредством списков смежности. Списком смежности для вершины i называется список всех вершин, смежных с вершиной i, причем определенным образом упорядоченный. Таким образом, граф G можно представить посредством массива HEAD (Заголовок), чей элемент HEAD[i] является указателем на список смежности вершины i. Представление графа с помощью списков смежности требует для хранения объем памяти, пропорциональный сумме количества вершин и количества дуг. Если количество дуг имеет порядок О(n), то и общий объем необходимой памяти имеет такой же порядок. Но и для списков смежности время поиска определенной дуги может иметь порядок О(n), так как такой же порядок может иметь количество дуг у определенной вершины.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 372. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
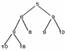
 Другими словами, максимально возможная сбалансированность двоичного дерева здесь понимается в том смысле, чтобы дерево было как можно "ближе" к полному двоичному дереву. На нижнем уровне, где некоторые листья могут отсутствовать, требуется, чтобы все отсутствующие листья в принципе могли располагаться только справа от присутствующих листьев нижнего уровня. Более существенно, что дерево частично упорядочено. Это означает, что приоритет узла v не больше приоритета любого сына узла v, где приоритет узла - это значение приоритета элемента, хранящегося в данном узле. Из рисунка видно, что малые значения приоритетов не могут появиться на более высоком уровне, где есть большие значения приоритетов. Например, на третьем уровне располагаются приоритеты 6 и 8, которые меньше приоритета 9, расположенного на втором уровне. Но родитель узлов с приоритетами б и 8, расположенный на втором уровне, имеет (и должен иметь) по крайней мере не больший приоритет, чем его сыновья. При выполнении функции DELETEMIN возвращается элемент с минимальным приоритетом, который, очевидно, должен быть корнем дерева. Но если просто удалить корень, то тем самым разрушится дерево. Чтобы не разрушить дерево и сохранить частичную упорядоченность значений приоритетов на дереве после удаления корня, необходимо выполнить следующее: сначала находим на самом нижнем уровне самый правый узел и временно помещаем его в корень дерева. На рисунке показаны изменения, сделанные на дереве после удаления корня. Затем этот элемент спускаем по ветвям дерева вниз (на более низкие уровни), по пути меняя его местами с сыновьями, имеющими меньший приоритет, до тех пор, пока этот элемент не станет листом или не встанет в позицию, где его сыновья будут иметь по крайней мере не меньший приоритет. Т.о., надо поменять местами корень и его сына, имеющего меньший приоритет, равный 5. В результате получим дерево:
Другими словами, максимально возможная сбалансированность двоичного дерева здесь понимается в том смысле, чтобы дерево было как можно "ближе" к полному двоичному дереву. На нижнем уровне, где некоторые листья могут отсутствовать, требуется, чтобы все отсутствующие листья в принципе могли располагаться только справа от присутствующих листьев нижнего уровня. Более существенно, что дерево частично упорядочено. Это означает, что приоритет узла v не больше приоритета любого сына узла v, где приоритет узла - это значение приоритета элемента, хранящегося в данном узле. Из рисунка видно, что малые значения приоритетов не могут появиться на более высоком уровне, где есть большие значения приоритетов. Например, на третьем уровне располагаются приоритеты 6 и 8, которые меньше приоритета 9, расположенного на втором уровне. Но родитель узлов с приоритетами б и 8, расположенный на втором уровне, имеет (и должен иметь) по крайней мере не больший приоритет, чем его сыновья. При выполнении функции DELETEMIN возвращается элемент с минимальным приоритетом, который, очевидно, должен быть корнем дерева. Но если просто удалить корень, то тем самым разрушится дерево. Чтобы не разрушить дерево и сохранить частичную упорядоченность значений приоритетов на дереве после удаления корня, необходимо выполнить следующее: сначала находим на самом нижнем уровне самый правый узел и временно помещаем его в корень дерева. На рисунке показаны изменения, сделанные на дереве после удаления корня. Затем этот элемент спускаем по ветвям дерева вниз (на более низкие уровни), по пути меняя его местами с сыновьями, имеющими меньший приоритет, до тех пор, пока этот элемент не станет листом или не встанет в позицию, где его сыновья будут иметь по крайней мере не меньший приоритет. Т.о., надо поменять местами корень и его сына, имеющего меньший приоритет, равный 5. В результате получим дерево:  Это дерево уже является частично упорядоченным и его дальше не надо менять. Если при таком преобразовании узел v содержит элемент с приоритетом а и его сыновьями являются элементы с приоритетами b и с, из которых хотя бы один меньше а, то меняются местами элемент с приоритетом а и элемент с наименьшим приоритетом из b и с. В результате в узле v будет находиться элемент с приоритетом, не превышающим приоритеты своих сыновей.
Это дерево уже является частично упорядоченным и его дальше не надо менять. Если при таком преобразовании узел v содержит элемент с приоритетом а и его сыновьями являются элементы с приоритетами b и с, из которых хотя бы один меньше а, то меняются местами элемент с приоритетом а и элемент с наименьшим приоритетом из b и с. В результате в узле v будет находиться элемент с приоритетом, не превышающим приоритеты своих сыновей.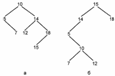 Дерево двоичного поиска - это двоичное дерево, узлы которого помечены элементами множеств (мы также будем говорить, что узлы дерева содержат или хранят элементы множества). Определяющее свойство дерева двоичного поиска заключается в том, что все элементы, хранящиеся в узлах левого поддерева любого узла х, меньше элемента, содержащегося в узле х, а все элементы, хранящиеся в узлах правого поддерева узла х, больше элемента, содержащегося в узле х.
Дерево двоичного поиска - это двоичное дерево, узлы которого помечены элементами множеств (мы также будем говорить, что узлы дерева содержат или хранят элементы множества). Определяющее свойство дерева двоичного поиска заключается в том, что все элементы, хранящиеся в узлах левого поддерева любого узла х, меньше элемента, содержащегося в узле х, а все элементы, хранящиеся в узлах правого поддерева узла х, больше элемента, содержащегося в узле х. Если узел node имеет двух сыновей, то мы просто делаем элемент х третьим сыном, помещая его в правильном порядке среди других сыновей. Осталось переписать два числа в узле node в соответствии с новой ситуацией.
Если узел node имеет двух сыновей, то мы просто делаем элемент х третьим сыном, помещая его в правильном порядке среди других сыновей. Осталось переписать два числа в узле node в соответствии с новой ситуацией.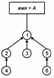
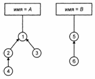 Каждый узел, за исключением корней деревьев, имеет указатель на своего родителя. Корни содержат как имя компонента-множества, так и элемент этого компонента. Отображение из множества имен к корням деревьев позволяет получить доступ к любому компоненту. Чтобы определить имя компонента, которому принадлежит элемент х, сначала с помощью отображения (т.е. массива, который не показан на рис.) получаем указатель на узел, соответствующий элементу х. Далее следуем из этого узла к корню дерева и там читаем имя множества.
Каждый узел, за исключением корней деревьев, имеет указатель на своего родителя. Корни содержат как имя компонента-множества, так и элемент этого компонента. Отображение из множества имен к корням деревьев позволяет получить доступ к любому компоненту. Чтобы определить имя компонента, которому принадлежит элемент х, сначала с помощью отображения (т.е. массива, который не показан на рис.) получаем указатель на узел, соответствующий элементу х. Далее следуем из этого узла к корню дерева и там читаем имя множества. Операция слияния делает корень одного дерева сыном корня другого. Например, при слиянии множеств А и В, когда результат слияния получает имя А, узел 5 становится сыном узла 1.
Операция слияния делает корень одного дерева сыном корня другого. Например, при слиянии множеств А и В, когда результат слияния получает имя А, узел 5 становится сыном узла 1. Однако неупорядоченные слияния могут привести к результату в виде дерева из n узлов, которое будет простой цепью узлов. В этом случае выполнение оператора FIND для любого узла такого дерева потребует времени порядка О(n2). В этой связи заметим, что хотя слияние может быть выполнено за О(1) шагов, но в общей стоимости всех выполняемых операций может доминировать операция поиска. Поэтому, если надо просто выполнить m слияний и n поисков элементов, данный подход может быть не самым лучшим выбором.
Однако неупорядоченные слияния могут привести к результату в виде дерева из n узлов, которое будет простой цепью узлов. В этом случае выполнение оператора FIND для любого узла такого дерева потребует времени порядка О(n2). В этой связи заметим, что хотя слияние может быть выполнено за О(1) шагов, но в общей стоимости всех выполняемых операций может доминировать операция поиска. Поэтому, если надо просто выполнить m слияний и n поисков элементов, данный подход может быть не самым лучшим выбором.
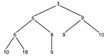
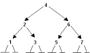 Среднее время выполнения этих операций будет также близким к O(log2n), так как в идеально сбалансированном дереве при полностью заполненных уровнях на последнем уровне находится больше половины узлов дерева. Например, последовательность значений 4, 6, 2, 1, 5, 3, 7 дает следующее идеально сбалансированное дерево:
Среднее время выполнения этих операций будет также близким к O(log2n), так как в идеально сбалансированном дереве при полностью заполненных уровнях на последнем уровне находится больше половины узлов дерева. Например, последовательность значений 4, 6, 2, 1, 5, 3, 7 дает следующее идеально сбалансированное дерево: Уровень 0 Для каждого узла дерева можно определить показатель
Уровень 0 Для каждого узла дерева можно определить показатель
 от узла с нарушенной балансировкой Выполняется, когда «перевес» идет по пути R-R от узла с нарушенной балансировкой.
от узла с нарушенной балансировкой Выполняется, когда «перевес» идет по пути R-R от узла с нарушенной балансировкой.

 Одинарный RL-поворот. Выполняется, когда «перевес» идет по пути R-L от узла с нарушенной балансировкой.
Одинарный RL-поворот. Выполняется, когда «перевес» идет по пути R-L от узла с нарушенной балансировкой.

