
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Простейшие уравнения с параметром.Уравнения с параметром. Линейное уравнение – это уравнение вида: ах = b, где a и b– некоторые постоянные. При решении линейных уравнений, получаем различное количество корней уравнения. Чтобы понять логику решения линейного уравнения с параметрами рассмотрим решение следующих частных уравнений. Пример 1. Решить уравнение 3х = - 15 . Решение: Т.к. а = 3, а b = - 15, то х = - 15 : 3(деление возможно, 3≠0); х = -5. Проверка: 3 ( -5) = - 15 0; - 15 = - 15(верное), то -5 является корнем исходного уравнения  Ответ: -5 Пример 2. Решить уравнение 0х = 0 Решение: 0 = 0(верное при любом значении переменной х ), то корнем уравнения является любое число. Ответ: х - любое число Пример 3.Решить уравнение 0х= 7 Решение: 0 = 7 (не верно при любом значении х), уравнение корней не имеет. Ответ: хЄ Вывод: 1)Если а≠0, то уравнение имеет единственный корень: х = 2) Если а = 0 и b = 0, то корнем уравнения ах= bявляется любое число. 3) Если а = 0,b≠0, то уравнение ах= bне имеет корней, хЄ Если а и b не принимать конкретными значениями, то, говорят, что а и b – это параметры в уравнении ах=b, а само уравнение ах=b - уравнение с параметрами. Однако овладеть методикой решения уравнений с параметром мне кажется очень полезным: оно существенно повышает уровень логической подготовки учащихся, позволяет чуть по-новому, как бы изнутри взглянуть на линейную зависимость, подробно анализируемую школьной программой. Многие учащиеся воспринимают параметр, как «обычное» число. Действительно, в некоторых уравнениях параметр можно считать постоянной величиной, но эта постоянная величина принимает неизвестные значения! Поэтому необходимо рассматривать уравнение при всех возможных значениях этой постоянной. С параметрами семиклассники встречаются уже при введении некоторых понятий. В качестве примеров рассмотрим следующие объекты: - функция прямая пропорциональность: y = kx (x и y переменные, k– параметр, k - линейная функция: y = kx+b (x и y – переменная, k и b – параметры); - линейное уравнение: ax+b=0 (x – переменная, aи b – параметры, a К уравнениям с параметрами, рассматриваемым в школьном курсе, можно отнести, например, поиск решений линейных уравнений в общем виде, исследование количества их корней в зависимости от значений параметров.Этот небольшой класс задач, конечно, многим не позволяет усвоить главное: параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойную природу. С одной стороны, с параметром работаем как с числом, с другой – это неизвестное. Так, деление на выражение, содержащее параметр, без предварительных исследований невозможно. Как правило, результаты этих исследований влияют и на решение, и на ответ. Основное, что нужно усвоить при первом знакомстве с параметром, - это необходимость осторожного, даже деликатного обращения с фиксированным, но неизвестным числом. Определение уравнения с параметром: «Пусть дано равенство с переменными х, а: f (x; а) = 0. Если ставится задача для каждого действительного значения а решить это уравнение относительно х, то уравнение f (х; а) = 0 называется уравнением с переменной х и параметром а. Решить уравнение с параметром а – это значит, для каждого значения а найти значение х, удовлетворяющие этому уравнению». Назовем контрольными значения параметра те значения, при которых обращается в нуль коэффициент при х в линейном уравнении. Рассмотрим алгебраический способ решения линейного уравнения. Простейшие уравнения с параметром. 1.Простейшие уравнения с параметром. Рассмотрим решение линейных уравнений, если параметр является свободным членом. Пример 4. Решить уравнение x – a = 0. Ответ: x = a, при любом a Пример 5. Решить уравнение 5x = a.Ответ: x = 1) Вывод: если параметр является свободным членом в уравнении, то уравнение всегда имеет один корень. Подобные упражнения помогают учащимся привыкнуть к параметру, к необычной форме ответов при решении уравнений. Замечу, что даже такие, казалось бы, совершенно элементарные уравнения часто требуют от учителя подробных комментариев и терпеливых объяснений. 2. В качестве второго шага, рассмотрим уравнения с параметром, где выделим уравнения с небольшим числом легко угадываемых ветвлений. Пример 6.Решить уравнение0•х = а. Ответ: при а при а = 0, х – любое из множества R. Пример 7. Решить уравнение. |x| = a. Ответ: при а при а = 0, х = 0, при а 3.Рассмотрим уравнения с параметром, где параметр – это коэффициент линейного уравнения, и, он может имеет вид алгебраического выражения. Пример 8.Решить уравнение ах = 1. Решение: Найдем контрольные значения параметра для коэффициента при х, а=0. Решение данного уравнения сведем к одному из случаев примеры 1-3. 1) Если а=0, то уравнение примет вид: 0х=1, а это уравнение не имеет корней. 2) Если а≠0, то деление на авозможно и х = Ответ: Ø приа =0; Пример 9. Решить уравнение (а-3)х=1. Решение: Найдем контрольные значения параметра для коэффициента при х,т.е. а-3=0, то а=3.Решение данного уравнения сведем к одному из трех случаев. (примеры 1-3). 1)Если а=3, то а-3=0, и уравнение (а-3)х=1примет вид 0х=1, а это уравнение корней не имеет. 2)Если а ≠3, то то деление на авозможно и х= Ответ: Ø,приа =3; Рассмотрим уравнения с параметром, где коэффициент линейного уравнения и свободный член содержат параметр. Пример 10. Решить уравнение (а-2)х=а-2. Решение: Найдем контрольные значения параметра для коэффициента при х , т.е.а-2=0, тоа =2. 1) Если а=2, то а-2=0, и уравнение (а -2)х=а -2примет вид 0х=0, х – любое число. 2) Если а≠2, то деление наавозможнох= Ответ: любое число, при а=2; 1, при а≠2 Пример 11. Решить уравнение b х + 1=2b + х. Решение: Приведем данное уравнение b х + 1=2b + х к виду ах =b. b х – x=2b - 1 (b – 1)х=2b - 1 Найдем контрольные значения параметра для коэффициента при х, b – 1=0, b=1. Если b=1,то b – 1=0, то уравнение (b – 1)х=2b - 1 примет вид 0х=1, корней нет 1) Если b≠1, тоb – 1≠0 деление возможно наb – 1 и х= Ответ: Ø, при b=1; Пример 12. Решить уравнение ( Решение: ( Найдем контрольные значения параметра для коэффициента при х, т.е.
1)Если b=1,то 2)Если b=0,то 3)Если b≠1 и b≠0, то деление наb(b-1) возможно и х= Ответ: любое число, при b=1;
Пример 13. Решить уравнение Решение:Приведем данное уравнение
( Найдем контрольные значения параметра для коэффициента при х,
1) Если а=0, то 2) Если а=1, то 3) Если а≠0 и а≠1, то х= Ответ: любое число, при а=1;
Данные выше примеры позволили увидеть, как изменяется вид рассматриваемого линейного уравнения с изменением значения параметра и влияние параметра как переменной на значение корней и их количество.
Графический способ решения линейного уравнения с параметром. Рассмотрим геометрическую интерпретацию решения линейного уравнения с параметрами kx+b=0. Графический способ определения числа корней уравнения в зависимости от входящего в него параметра является более удобным, чем аналитический. Количество корней линейного уравнения kx+b=0 зависит от расположения прямых у= kx+b и у=0, но второе уравнение можно записать в виде у= 0x+0, где k=0, b=0. Две прямые на плоскости могут либо пересекаться (только в одной точке), либо быть параллельными, либо совпадать, а соответственно уравнение kx+b=0 может иметь 1 корень, не иметь корней, или иметь бесчисленное множество корней. Решением уравнения kx+b=0 являются абсциссы точек пересечения прямых, заданных уравнениями у= kx+b и у= 0x+0. Рассмотрим эти случаи расположения прямых, и подтвердим, от чего зависит решение уравнения. 1 случай: Пусть в уравнении у= kx+b, параметр b – некоторое фиксированное число, k – любое, k≠0. Это уравнение на плоскости задает множество прямых, проходящих через точку (0; b). k – угловой коэффициент прямой и он один и тот же для данного множество прямых. Т.к. k≠0, то прямые, заданные уравнениями у= kx+b и у= 0x+0, пересекаются.
Рис.1 b |
|||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 182. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
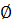
 ( ах = b; ах = b; х = b : а; х=
( ах = b; ах = b; х = b : а; х= 
 0);
0); , при любомa.
, при любомa. = aОтвет: x = 2a, при любом a.
= aОтвет: x = 2a, при любом a.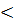 0, корней нет,
0, корней нет, 0, х =
0, х =  а.
а.
 0.
0.
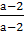 =1
=1
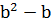 )х=
)х=  – 1.
– 1. =0, уравнение(
=0, уравнение(  =0, уравнение примет вид 0х= - 1, корней нет
=0, уравнение примет вид 0х= - 1, корней нет =
= 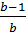
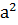 х=а(х+2) – 2
х=а(х+2) – 2 -а=0, и уравнение (
-а=0, и уравнение (  =
= 




 Вывод: уравнение kx+b=0 при k≠0 имеет один корень. ( рис.1)
Вывод: уравнение kx+b=0 при k≠0 имеет один корень. ( рис.1)