Такт роботи машини Тьюрінга

Міністерство освіти І науки України

національний університет “Львівська політехніка”

Кафедра ЕОМ

Програмування машин Тьюрінга

Методичні вказівки

До лабораторної роботи № 1

з дисципліни

" AЛГОРИТМИ ТА МЕТОДИ ОБЧИСЛЕНЬ"

для студентів напряму

6.050102 “Комп’ютерна інженерія”

Львів – 2012

Методичні вказівки до комплексу лабораторних робіт з дисципліни "Алгоритми та методи обчислень" для підготовки студентів напряму 6.050102 “Комп’ютерна інженерія” / Укл. Т.А.Матвейчук – Львів: Видавництво НУ “Львівська політехніка”, 2012 – 22 с.

Укладач:                           Матвейчук Т.А., ст. викладач каф.ЕОМ

Відповідальний

за випуск:                         Мельник А.О., д-р техн. наук, проф.

Рецензенти:                      Мороз І.В., ст. викладач каф.ЕОМ

                                           Юрчак І.Ю., доцент кафедри САПР, к.т.н.

МЕТА РОБОТИ

Вивчити принципи роботи машин Тюринга, набути практичних навичок програмування машин Тьюрінга.

ТЕОРЕТИЧНІ ВІДОМОСТІ

Теорія алгоритмів - одне з основних понять математики та інформатики. Навіть походження
самого терміна «алгоритм» пов'язане з математикою. Відомо, що основна особливість всіх обчислювальних машин полягає в тому, що в основі їх роботи лежить програмний принцип управління. Це означає, що для вирішення як найпростішого, так і найскладнішого завдання користувачеві необхідно використовувати перелік інструкцій або команд, дотримуючись яких крок за кроком комп'ютер видасть необхідний результат. Таким чином, для того, щоб вирішувати завдання на комп'ютері, його необхідно спочатку алгоритмізувати. Саме алгоритмічний принцип і лежить в основі роботи всіх комп'ютерів.

Поняття алгоритму

В старому трактуванні алгоритм - це точний набір інструкцій, що описують послідовність дій деякого виконавця для досягнення результату, Розв'язок деякого завдання за кінцевий час. У зв'язку з розвитком паралельності в роботі комп'ютерів слово «послідовність» стали заміняти більше загальним словом «порядок». Це пов'язане з тим, що якісь дії алгоритму повинні бути виконані тільки один за одним, але якісь можуть бути й незалежними.

Поняття алгоритму необов'язково відноситься до комп'ютерних програм, так, наприклад, чітко описаний рецепт готування блюда також є алгоритмом, у такому випадку виконавцем є людина. Однак найчастіше як виконавець виступає комп'ютер.

Єдиного «істинного» визначення поняття «алгоритм» немає.

«Алгоритм - це всяка система обчислень, що виконуються по строго визначеним правилам, які після певного числа кроків свідомо приводять до Розв'язок поставленого завдання.» (А. Колмогоров)

«Алгоритм - це точне розпорядження, яке визначає обчислювальний процес, що йде від варійованих вихідних даних до шуканого результату.» (А. Марков)

«Алгоритм - строго детермінована послідовність дій, що описує процес перетворення об'єкта з початкового стану в кінцеве, записана за допомогою зрозумілих виконавцеві команд.» (М. Угринович)

«Алгоритм - це послідовність дій, спрямованих на одержання певного результату за кінцеве число кроків.» (ROXANstudio)

«Алгоритм є формалізована послідовність дій (подій). Алгоритм може бути записаний словами і зображений схематично. Практично будь-яка невипадкова повторювана дія піддається опису через алгоритм.» ([grey_olli])

«Алгоритм - однозначно, доступно і коротко описана послідовність процедур для відтворення процесу з обумовленим завданням алгоритму результатом при заданих початкових умовах. Універсальність (або спеціалізація) алгоритму визначається застосовністю і надійністю даного алгоритму для Розв'язок нестандартних завдань.»

Машина Тьюрінга

Формальні визначення алгоритму з'явились в тридцятих-сорокових роках 20 століття. Одним із перших було визначення англійського математика Алана Тьюрінга, який у 1936 році описав схему деякої абстрактної машини і запропонував називати алгоритмами те, що вміє робити така машина. При цьому визначенні, якщо щось не може бути зроблено машиною Тьюрінга, це вже не алгоритм. Інакше кажучи, Тьюрінг формалізував правила виконання дій за допомогою опису роботи деякої конструкції. Машина Тьюрінга (МТ) – математичне поняття, введене для формального уточнення інтуїтивного поняття алгоритму.

Метою створення абстрактної уявлюваної машини було отримання можливості доказу існування або неіснування алгоритмів розв'язання різних задач. Керуючись цією метою, Тьюрінг шукав як умога більш просту, «бідну» алгоритмічну схему, аби тільки вона була універсальною.

Машина Тьюрінга - це строга математична побудова, математичний апарат (подібний, наприклад, апарату диференціальних рівнянь), створений для розв'язання певних задач. Цей математичний апарат був названий «машиною» з тієї причини, що по опису його складових частин і функціонуванню він схожий на обчислювальну машину. Принципова відмінність машини Тьюрінга від обчислювальної машини полягає в тому, що її запам'ятовувальний пристрій являє собою нескінченну стрічку, а у реальних обчислювальних машин запам'ятовувальний пристрій може бути як завгодно великим, але обов'язково кінцевим. Машину Тьюрінга не можна реалізувати саме через нескінченність її стрічки. У цьому сенсі вона могутніша будь-якої обчислювальної машини.

Машина Тьюрінга являє собою найпростішу обчислювальну машину з лінійною пам'яттю, яка за допомогою послідовності елементарних дій перетворює вхідні дані. Елементарність дій полягає в тім, що дія міняє лише невеликий об'єм даних у пам'яті (у випадку машини Тьюрінга - лише одну комірку), і кількість можливих дій кінцева. Незважаючи на простоту машини Тьюрінга на ній можна обчислити все, що можна обчислити на будь-якій іншій машині, яка здійснює обчислення за допомогою послідовності елементарних дій. Ця властивість називається повнотою. Машина Тьюрінга може виконувати всі можливі перетворення слів, реалізуючи тим самим всі можливі алгоритми.

Один зі способів доказу того, що алгоритми обчислення, який можна реалізувати на одній машині, можна реалізувати й на інший, - це імітація першої машини на другій. Імітація полягає в наступному. На вхід другої машини подається опис програми (правил роботи) першої машини D і вхідн дані X, які повинні були надійти на вхід першої машини. Потрібно описати таку програму (правила роботи другої машини), яка б у результаті обчислень на виході видавала б те саме, що й повернула б перша машина, якби одержала на вхід дані X. На машині Тьюрінга можна імітувати всіх інших виконавців, які певним чином реализують процес покрокового обчислення, у якому кожний крок обчислення досить елементарний. На машині Тьюрінга можна імітувати машину Поста, нормальні алгоритми Маркова і будь-яку програму для звичайних комп'ютерів, що перетвориє вхідні дані у вихідні по деякому алгоритму. У свою чергу, на різних абстрактних виконавцях можна імітувати Машину Тьюрінга. Виконавці, для яких це можливо, називаються повними по Тьюрінгу.

Багатство можливостей машини Тьюрінга проявляється в тому, що якщо якісь алгоритми А і В реалізуються машинами Тьюрінга, то можна побудувати машини Тьюрінга, що будуть реалізовувати різні композиції алгоритмів А і В. Наприклад, «Виконати А, потім виконати В» або «Виконати А. Якщо в результаті вийшло слово «так», то виконати В. У противному випадку не виконувати В» або «Виконувати по черзі А, В, поки В не дасть відповідь 0». Очевидно, що такі композиції також є алгоритмами, тому їхня реалізація за допомогою машини Тьюрінга підтверджує, що конструкція Тьюрінга є універсальним виконавцем.

Всякий алгоритм може бути реалізований відповідною машиною Тьюрінга. Всі алгоритми, придумані людством протягом сторіч можуть бути реалізовані машиною Тьюрінга. Кожний алгоритм призначений для якогось конкретного виконавця, у кожного виконавця є своя система команд, є своє коло задач. Тьюрінгом же був побудований універсальний виконавець, що може вирішити будь-яку відому задачу. Цей фундаментальний результат був отриманий у той час, коли універсальних обчислювальних машин ще не існувало. Більше того, сам факт побудови уявлюваного універсального виконавця дозволив висловити припущення про доцільність побудови універсальної обчислювальної машини, яка б могла вирішувати будь-які задачі за умови відповідного кодування вхідних даних і розробки відповідної програми дій виконавця.

Структура машини Тьюрінга

Машина Тьюрінга (МТ) складається із двох частин - стрічки та каретки:

стрічка:	a b b	a b b
каретка:

Стрічка використовується для зберігання інформації, що складається з символів зовнішнього алфавіту А. Вона нескінченна в обидва боки і розбита на комірки, які ніяк не нумеруються і не іменуються. В кожній комірці може бути записаний один символ або нічого не записано. Вміст комірки може мінятись - в неї можна записати інший символ або стерти символ, який там знаходиться.

Домовимось порожній вміст комірки називати символом «порожньо» і позначати як . У зв'язку із цим зображення стрічки, показане на малюнку справа, буде таким самим, як і на малюнку зліва. Для обох цих зображень зовнішній алфавіт визначається як А={a_{0 ,} a _, b}. Така домовленість зручна тим, що операцію стирання символу в деякій комірці можна розглядати як запис у цю комірку символу , тому замість довгої фрази «записати символ у комірку або стерти символ, що там знаходиться» можна говорити просто «записати символ у комірку».

Каретка - це активна частина МТ. В кожний момент вона розміщується під однією з комірок стрічки і розпізнає її вміст; вміст сусідніх та інших комірок каретка не бачить. Крім того, в кожний момент каретка перебуває в одному із станів, які будемо позначати буквою q з номерами: q₀, q₁, q₂ і т.д., які складають алфавіт внутрішніх станів Q = {q₀, q₁ , ... , q_m},. Перебуваючи в деякому стані, каретка виконує якусь певну операцію (наприклад, переміщується вправо по стрічці, заміняючи всі символи b на a), перебуваючи в іншому стані - іншу операцію.

Такт роботи машини Тьюрінга

МТ працює тактами, які виконуються один за одним. На кожному такті МТ виконує три наступні дії, причому обов'язково в зазначеному порядку:

 1) записує деякий символ  в комірку (зокрема, може бути записаний той самий символ, що й був у ній, тоді вміст цієї комірки не міняється);

 2) переміщується на одну комірку вліво (позначається як L, від Left), або на одну комірку вправо (позначається як R, від Right), або залишається нерухливим (не позначається ніяк).

 3) переходить в деякий стан q_i (зокрема, може залишитись в попередньому стані).

Формально дії одного такту будемо записувати у вигляді:

 ,  

або   ,  

або      .

Наприклад, такт означає запис символа 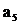 у комірку, переміщення на одну комірку вліво і перехід у стан .