
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задания к индивидуальной работе ⇐ ПредыдущаяСтр 2 из 2 1. Разработайте функциональную схему машины Тьюринга для решения указанной задачи. 2. Постройте программу (в виде протокола, таблицы соответствия и в виде графа) машины Тьюринга, вычисляющую следующую функцию. 3. Используя базис элементарных машин с помощью операций композиции, ветвления и зацикливания постройте машины, вычисляющие функции: Замечание. Для вариантов 1-10 дополнительно следует использовать и машины М1, М2, М3, вычисляющие соответственно функции f(x)=2∙x, f(x, y)=x+y, f(x, y)=xºy, Вариант 1 1. На информационной ленте машины Тьюринга содержится массив символов «+». Необходимо разработать функциональную схему машины Тьюринга, которая каждый второй символ «+”» заменит на «–». Каретка в состоянии q0 находится где-то над указанным массивом. 2. f(x) = x + 5. 3. f(x, y)= x ∙ y. Вариант 2 1. Дано число n в восьмеричной системе счисления. Разработать программу для машины Тьюринга, которая увеличивала бы заданное число n на 1. 2. f(x) = 4∙x. 1. f(x, y)= 2 ∙ (x¸y), ), где знак «¸ » – знак ограниченного вычитания Вариант 3 1. Дан массив из открывающихся и закрывающихся скобок. Построить программу для машины Тьюринга, которая удаляла бы пары взаимных скобок. Например, дано : « ) ( ( ) ( ( ) », надо получить : « ) . . . ( ( . ». 2. f(x) = 2 – x. 3. f(x, y)=2∙ x + y Вариант 4 1. Дана десятичная запись натурального числа n>1. Разработать программу для машины Тьюринга, которая уменьшала бы заданное число n на 1. При этом запись числа n–1 не должна содержать левый нуль, например, 100–1=99, а не 099. Начальное положение головки – правое. 2. f(x) = 5 – x. 3. f(x, y)= [x / y]. Вариант 5 1. На информационной ленте машины Тьюринга в трех секциях в произвольном порядке записаны 3 различные буквы: «A», «B» и «C». Каретка в состоянии q0 обозревает букву, расположенную справа. Необходимо составить функциональную схему машины Тьюринга, которая сумеет поменять местами крайние буквы.  2. f(x) = x – 3. 3. f(x)= 2∙x + 5. Вариант 6 1. Дана строка из букв «a» и «b». Разработать программу для машины Тьюринга, которая переместит все буквы «a» в левую, а буквы «b» – в правую части строки. Каретка находится над крайним левым символом строки. 2. f(x) = |x – 3|. 2. f(x)= x¸3, ), где знак «¸ » – знак ограниченного вычитания 3. Вариант 7 1. Даны два целых положительных числа в десятичной системе счисления. Сконструировать машину Тьюринга, которая будет находить разность этих чисел, если известно, что первое число больше второго, а между ними стоит знак «–». Каретка находится над левой крайней цифрой левого числа. 2. f(x) = |k ∙ x – 3|. 3. f(x, y)= 2∙(x + y) ¸ (x ¸ y), где знак «¸ » – знак ограниченного вычитания Вариант 8 1. Дана конечная последовательность меток, записанных в клетки ленты подряд, без пропусков. Необходимо разработать программу для машины Тьюринга, которая будет записывать в десятичной системе счисления число этих меток. 2. . f(x) = x – k. 3. Вариант 9 1. На ленте машины Тьюринга находится число, записанное в десятичной системе счисления. Умножить это число на 2, если каретка находится над крайней левой цифрой числа. 2. f(x) = 3 ∙ x – 2. 3. f(x,y), удовлетворяющей условиям Вариант 10 1. Сконструировать машину Тьюринга, которая выступит в качестве двоично-восьмеричного дешифратора. 2. f(y) = 2∙ y – 1. 3. f(x) = my[(x + y) ¸ 5 = 0], где Вариант 11 1. На ленте машины Тьюринга находится целое положительное число, записанное в десятичной системе счисления. Найти произведение этого числа на число 11. Каретка обозревает крайнюю правую цифру числа. 2. f(y) = |2∙ y – 1|. 3. f(х) = x + 5. Вариант 12 1. Даны два натуральных числа n и m, заданных в унарной системе счисления. Числа n и m представлены наборами символов «|», разделенных «\». В конце набора стоит «=». Разработать машину Тьюринга, которая будет производить деление нацело двух натуральных чисел n и m и находить остаток от деления. При этом результат должен быть записан следующим образом: после «=» должен находиться набор символов «|» частного (он может быть и пустым), после чего ставится знак «(», за которым следует набор символов «|» остатка от деления n на m. 2. f(x) = |x – k|. 3. f(х) = 3 ∙ x + 5. Вариант 13 1. Даны два натуральных числа m и n, представленных в унарной системе счисления. Соответствующие наборы символов «|» разделены «–», вслед за последним символом набора n стоит знак «=». Разработать машину Тьюринга, которая будет находить разность чисел m и n .При этом результат должен быть записан следующим образом: если m>n , то справа от «=» должны стоять знак «+» и набор символов «|» в количестве m–n; если m=n, то справа от знака «=» должна стоять пустая клетка; если m<n, то справа от «=» должны стоять знак «–» и набор символов «|» в количестве n–m. 2. f(x) = 2 ∙ x + 3. 3. f(х) = x ¸ 5, где Вариант 14 1. Даны два целых положительных числа в различных системах счисления, одно – в троичной системе, другое – в десятичной. Разработать машину Тьюринга, которая находит сумму этих чисел в десятичной системе счисления. 2. f(y) = k ∙y + 1. 3. Вариант 15 1. На информационной ленте машины Тьюринга находится десятичное число. Найти результат целочисленного деления этого числа на 2. 2. f(y) = ∙y + 2. 3. Вариант 16 1. На ленте машины Тьюринга находится слово, состоящее из букв латинского алфавита 2. . f(x) = x2. 3. Вариант 17 1. На информационной ленте машины Тьюринга находится массив, состоящий только из символов A и B. Сжать массив, удалив из него все элементы B. 2. f(x, y) = x / y. 3. Вариант 18 1. На ленте машины Тьюринга находится десятичное число. Определить делится это число на 5 без остатка. Если делится, то записать справа от числа слово «да», если нет – «нет». Каретка находится где-то над числом. 2. f(x) = x2 – 1. 3. Вариант 19 1. На ленте машины Тьюринга записано число в десятичной системе счисления. Каретка находится над крайней правой цифрой. Записать цифры этого числа в обратном порядке. 2. f(x, y) = x ∙ y. 3. f(x) = x!. Вариант 20 1. Число n задано на ленте машины Тьюринга массивом меток. Преобразовать значение n по формуле: 2. Построить машину Тьюринга, вычисляющую нуль-функцию 01(x) = 0 в алфавите {L, 1}. 3. f(х) = 4 ∙ x + 1. Вариант 21 1. На ленте машины Тьюринга находится массив 2*N меток. Уменьшить этот массив в 2 раза. 2. Функцию выбора 3. Вариант 22 1. Число n задано на ленте машины Тьюринга массивом меток. Преобразовать значение n по формуле: 2. Функцию выбора 3. f(y) = 3 ∙ y + 2. Вариант 23 1. Даны два натуральных числа n и m, представленные в унарной системе счисления. Между этими числами стоит знак «?». Выяснить отношение m и n, т.е. знак «?» заменить на один из подходящих знаков «>», «<», «=». 2. Функцию выбора 3. Вариант 24 1. Найти произведение двух натуральных чисел m и n, заданных в унарной системе счисления. Соответствующие наборы символов «|» разделены знаком «*», справа от последнего символа правого члена стоит знак «=». Поместить результат умножения этих чисел вслед за знаком «=». 2. Реализовать на МТ алгоритм вычисления функции f(n) = n +2, где nÎN. Указание: Взять множество состояний Q = {q0, q1, q2}. Число n на ленте МТ записывается в десятичной системе счисления. Состояние q1 заменяет последнюю цифру числа n, если эта цифра меньше 8, цифрой, на две единицы большей, и переходит в стоп-состояние. Если последняя цифра числа n равна 8, то ее заменить на 0 и перейти влево в состояние q2 . Состояние q2 добавляет к следующему разряду 1. Если же последняя цифра числа n равна 9, то ее заменить на 1 и перейти влево в состояние q2 . 3.
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 903. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

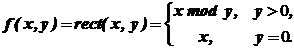
 где
где 


 . Подсчитать число букв «a» в данном слове и полученное значение записать на ленту левее исходного слова через пробел. Каретка обозревает крайнюю левую букву.
. Подсчитать число букв «a» в данном слове и полученное значение записать на ленту левее исходного слова через пробел. Каретка обозревает крайнюю левую букву.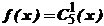 .
.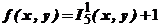
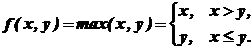
 . Каретка обозревает крайнюю левую метку.
. Каретка обозревает крайнюю левую метку. .
.
 . Каретка обозревает крайнюю левую метку.
. Каретка обозревает крайнюю левую метку. .
. .
.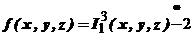 , где
, где  , где
, где