
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод математической индукцииЗадачи о числах. Делимость – Сегодня мы будем работать с 2 множествами. Множеством натуральных и целых чисел (на слайде изображены обозначения этих множеств:N={1,2,3,4…}–мн. натуральных чисел; Четность и нечетность –Какие числа называются четными? (– Числа, которые делятся на 2 нацело.) – Какие числа называются нечетными? (– Числа, которые при делении на 2 дают в остатке 1.) – Вспомним, как записываются четные и нечетные числа. (–n=2k, kÎZ – четные числа; n=2k+1, kÎZ – нечетные числа.)
–(стр.41 №57) Сумма 2ух целых чисел не четна. Четно или нечетно их произведение? (– Четно. Т.к. пусть n1+n2=2k1+(2k2+1). n1*n2=2k1*(2k2+1)=4k1k2+2k1. Первое слагаемое четно, второе слагаемое четно, значит сумма четна.) –(стр.42 №59)Можно ли разменять 25р., имея только рублевые, 3ехрублевые и 5тирублевые купюры, чтобы получилось 10 купюр? (– Нет, т.к. сумма 10ти нечетных чисел четна, а 25 нечетное число.) –(стр.43 №65) В вершинах куба расставили числа 1,2,3,4,5,6,7,8. На каждой грани записали сумму чисел в её вершинах, могут ли на гранях получиться 6 последовательных натуральных чисел? (– Попробуем просуммировать числа на всех гранях. Каждая вершина принадлежит 3ем граням куба, поэтому каждое из 8ми чисел в общей сумме утроится. 3(1+2+3+4+5+6+7+8)=108. Но среди любых 6ти последовательных натуральных чисел 3 четных и 3 нечетных. Следовательно, их сумма нечетна и не может быть равна 108.) 
Остатки – Что значит, разделит натуральное число nна натуральное число mс остатком? (– Разделить натуральное число nна натуральное число mс остатком означает найти такие числа kиrиз множества – Как при этом называется число r? (– r называется остатком от деления nна m.) – Какими свойствами обладает остаток? (– Остаток всегда меньше делителя. При делении натуральных чисел на заданное натуральное число может быть только конечное число различных остатков.) – Более подробно поговорим о возможных остатках при делении на 3 и попробуем обобщить наблюдения и для других делителей. Докажем 2 утверждения. – Утверждение 1: Сумма любых 2ух натуральных чисел и сумма их остатков от деления на 3 имеют одинаковые остатки при делении на 3. Доказательство: Пусть n1=k1*3+r1, n2=k2*3+r2. Тогда n1+n2=(k1+k2)*3+(r1+r2). Как поведет себя последняя сумма при делении на 3? Слагаемое (k1+k2)*3 поделиться нацело, а (r1+r2) можно представить в виде: r1+r2=k3*3+r3. После подстановки получим: n1+n2=(k1+k2+k3)+r3. Так что остаток от деления n1+n2 на 3 будет таким же, как остаток от деления r1+r2 на 3. – Утверждение 2: Произведение любых 2ух натуральных чисел и произведение их остатков от деления на 3 имеют одинаковые остатки при делении на 3. – Как будем проводить доказательство? (– Аналогично доказательству первого утверждения) – Проведите доказательство дома. – Что произойдет, если в утверждениях 1 и 2 тройку заменить любым другим натуральным числом? (– Утверждения будут справедливы.(В этом легко убедиться, проведя аналогичные рассуждения))
–(стр.48№72а) Найдите остаток от деления числа 22*50+44*10 на 3. (– Воспользуемся утверждениями 1 и 2. Заменим каждое из чисел на его остаток от деления на 3. Получим выражение 1*2+2*1. Это число равно 4 и дает остаток 1 при делении на 3. Значит, остаток от деления исходного числа на 3 также равен 1.) –(стр. 57 №82) Докажите, что не существует натуральных чисел aиb таких, что (– Рассмотрим возможные остатки левой и правой части от деления на 3. Число Признаки делимости – Вспомним известные нам признаки делимости в форме викторины «Верно ли, что…» 1) На 2 делятся все четные числа? (Да) 2) На 3 делятся числа, сумма цифр которых кратна 3? (Да) 3) На 4 делятся числа, две последние цифры которых нули или числа, не кратные 4? (Нет! На 4 делятся числа, две последние цифры которых нули или числа, кратные 4!) 4) На 5 делятся числа, оканчивающиеся на 5 или на 0? (Да) 5) На 6 делятся числа, которые делятся на 3? (Нет! На 6 делятся числа, которые делятся на 2 и на 3 одновременно! 81 делится на 3, но не делится на 6!) 6) Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7? (Да. 259 делится на 7 т.к. 25–(9*2)=25–18=7 делится на 7; 324 не делится на 7 т.к. 32–(4*2)=32–8=24 не делится на 7) 7) На 8 делятся числа, три последние цифры которых нули или числа, кратные 8? (Да) 8) На 9 делятся числа, сумма цифр которых кратна 3? (Нет! На 9 делятся числа, сумма цифр которых кратна 9!) 9) На 10 делятся числа, оканчивающиеся 0? (Да) 10) На 11 делятся числа, у которых сумма цифр, занимающих четные места, равна сумме цифр, занимающих нечетные места, или разность суммы цифр нечетных мест и суммы цифр четных мест кратна 11? (Да. 105787 делится на 11 т.к. 1+5+8=14 и 0+7+7=14, 14=14) 11) На 12 делятся числа, которые делятся на 4? (Нет! На 12 делятся числа, которые делятся на 3 и на 4 одновременно!) 12) Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13? (Да. 845 делится на 13, так как 84+(4*5) = 104 делится на 13) 13) На 14 делится числа, которые делятся на 7? (Нет! На 14 делятся числа, которые делятся на 2 и на 7 одновременно. 14) На 15 делится числа, которые делятся на 3 и на 5 одновременно? (Да) 15) На 25 делятся числа, две последние цифры которых нули или составляют число, кратное 25? (Да) 16) На разрядную единицу делятся числа, у которых количество нулей больше количества нулей разрядной единицы? (Нет!На разрядную единицу делятся числа, у которых количество нулей больше или равно количеству нулей разрядной единицы.)
–Делятся ли, следующие числа на 6, 9, 11 или 13? (1026, 151632, 35805, 9163627, 1710, 113724); –(стр.61 №90) Ковбой Джо зашел в бар и попросил у бармена бутылку виски за 3 доллара, трубку за 6 долларов, 3 пачки табака и 9 коробок непромокаемых спичек, цену которых он не знал. Бармен потребовал 11 долларов и 80 центов, на что Джо вытащил револьвер. Бармен поторопился исправить ошибку. Как Джо догадался, что бармен хотел его обсчитать? (–Стоимость всех покупок делиться на 3, а бармен назвал сумму не делящуюся на 3.) –(стр.79 №117) Число (–Запишем данное число по-другому – Делятся ли на 7 следующие числа?(259, 3245, 13265) Простые числа – Какие числа называются простыми? (– Простое число – натуральное число, имеющее ровно 2 натуральных делителя: себя и 1.) – Назовите наименьшее простое натуральное число. (– 2.) – Почему 1 не является простым числом? (– Так как имеет только один натуральный делитель.) – Если из множества натуральных чисел «изъять» 1 и все простые числа, то останутся …? (– Составные числа.) – Какое число называется составным? (– Если у него более 2ух различных натуральных делителей.)
– (стр.86 №129) Какие могут получиться остатки при делении простого числа большего, чем 3 на 6? (– p=6q+r.При делении на 6 могут быть остатки 0,1,2,3,4,5. Если r=0, то p – составное, так как делятся на 6. Если r =2, то p=6q+2 делятся на 2, следовательно, составное. Если r=3, тоp=6q+3 делятся на 3, составное. Если r=4, тоp=6q+4 делятся на 2, составное. Возможны остатки 1 и 5. 7=6*1+1, 11=6*5+5.)
Делители, НОД, НОК – Что называется делителем числа? (– Делителем числа А называется такое число В, на которое А делится без остатка) – Что называется общим делителем чисел А, В и С? (– Число, на которое делятся числа А, В и С) – Наибольшим общим делителем (НОД) чисел называется…? (– Наибольший общий делитель этих чисел) На слайде изображено: НОД (12,18) = 6, чтобы напомнить обозначение НОД. – По какому правилу находится НОД чисел? (–1 способ:Чтобы найти НОД нескольких чисел, необходимо: 1. Разложить все данные числа на простые множители; 2. Отметить одинаковые множители во всех разложениях; 3. Найти произведение отмеченных множителей, которое и есть наибольшим общим делителем этих чисел.
– 2 способ:Алгоритм Евклида. 1. Большее число делим на меньшее. 2. Если делится без остатка, то меньшее число и есть НОД. 3. Если есть остаток, то большее число заменяем на остаток от деления. 4. Переходим к пункту 1. Пример: – Что называется кратным числа? (– Кратным числа А называется такое число В, которое делится без остатка на А) – Что называется общим кратным нескольких чисел? (– Число, которое делится на каждое из этих чисел) – Наименьшее общее кратное (НОК) – это…? (– Наименьшее число, на которое делятся все данные числа) На слайде изображено: НОК(2,3,4,5,6,7,8) = 840, чтобы напомнить обозначение НОК – По какому правилу находится НОК? (–Чтобы найти НОК нескольких чисел, нужно: 1. Разложить числа на простые множители; 2. Перенести во множители искомого произведения самое большое разложение (произведение множителей самого большого числа из заданных), а потом добавить множители из разложения других чисел, которые не встречаются в первом числе или стоят в нем меньшее число раз; 3. Полученное произведение простых множителей будет НОК заданных чисел.)
–Найдите НОД(396,360) и НОК(396,360) (– Разложим на простые множители числа: 396=2*2*3*3*11, 360=2*2*2*3*3*5, НОК=396*2*5=3960, НОД=2*2*3*3=36) – Применяя алгоритм Евклида найдите НОД чисел: 35673287 и 7564. (– НОД(35673287,7564) = НОД(7564,1463) =НОД(1463,249)= НОД(249,218) = НОД(218,31) = НОД(31,1)=1) –(стр.96 №150) Докажите, что дробь (– НОД(30n+2, 12n+1)=НОД(18n+1, 12n+1)=НОД(12n+1, 6n)=НОД(6n,1)=1.Это означает, что у числителя и знаменателя больше нет общих делителей, то есть дробь несократима.) Последняя цифра – Рассмотрим последовательность степеней 2ки: 2,4,8,16,32,64… – Что мы можем заметить из данной записи? (– –Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то происходит зацикливание: (– 4.)
–(стр.99 №156) На какую цифру оканчивается число (– Выпишем последние цифры нескольких начальных степеней 7ки: 7, 9, 3, 1, 7… На пятом шаге последняя цифра повторилась, значит длинна цикла = 4 и надо разделить 777 на 4 с остатком. 777=194*4+1. И так последняя цифра числа будет 7.) –(стр.99 №157) Найдите остаток от деления (– Выпишем остатки от деления на 3 несколько начальных степеней 2ки.Может быть там тоже есть зацикливание. Вспомним утверждение 2 из раздела остатки. 2 делится на 3 с остатком 2, тогда Метод математической индукции – В чем суть ММИ? (– 1.[БАЗА] Показываем, что доказываемое утверждение верно для некоторых простейших частных случаев (n = 1) 2. [ПРЕДПОЛОЖЕНИЕ] Предполагаем, что утверждение доказано для первых K случаев. 3. [ШАГ] В этом предположении доказываем утверждение для случая n=K+1. 4. [ВЫВОД] Утверждение верно для всех случаев, то есть для всех n.)
–(стр.101 №163) Докажите, что для любого натурального nчисло (– 1) Проверим базу индукции.При n=1, 2) Пусть утверждение истинно для n=k. Докажем истинность утверждения при n=k+1. Подставим k+1 в данное выражение вместоn:
Домашнее задание №58 Сумма 3ех целых чисел четна. Четно или нечетно их произведение? (стр. 41) №69 У нескольких крестьян есть 128 овец. Если у кого-то из них оказывается не менее половины всех овец, остальные сговариваются и раскулачивают его: каждый берет себе столько овец, сколько у него уже есть. Если у 2их по 64 овцы, то раскулачивают кого-то одного из них. Произошло 7 раскулачиваний. Докажите, что в результате все овцы, собрались у одного крестьянина. (стр.44) №72(б) Найдите остатки от деления: 1) 1989*1990*1991+ 2) №95Скольконатуральных чисел от 5 до 41 делятся и на 2 и на 3? (стр.63) №130Докажите, что остаток от деления простого числа на 30 есть простое число или 1. (стр. 86) №158Найдите остаток от деления №166 Доказать, что для любого натурально nчисло Контрольная работа Вариант 1. Докажите, что сумма любых двух натуральных чисел и сумма их остатков от деления на 3 имеют одинаковые остатки при делении на 3. 2. Найти наименьшее натуральное число, которое при делении на 7 дает в остатке 6, а при делении на 9 остаток равен 8. 3. Найдите последнюю цифру числа
Вариант 1. Докажите, что произведение любых двух натуральных чисел и произведение их остатков от деления на 3 имеют одинаковые остатки при делении на 3. 2. Покупатель взял в магазине пакет молока, стоимостью 3,45 гривны,коробку творога, стоимостью 3,6 гривны, 6 пирожных и 3 килограмма сахара.Когда кассирша выбила чек на 29,6 гривны, покупатель потребовал проверить расчет и исправить ошибку.Как определил покупатель, что счет неверен? 3. Найдите последнюю цифру числа
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 311. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ={0,1,2,3…}; Z={…–2,–1,0,1,2,…}– мн. целых чисел). По ходу занятия мы вспомним: делимость чисел нацело и с остатком, четность и нечетность чисел, простые и составные числа, алгоритм Евклида, признаки делимости, НОД и НОК, взаимно простые числа и ММИ.
={0,1,2,3…}; Z={…–2,–1,0,1,2,…}– мн. целых чисел). По ходу занятия мы вспомним: делимость чисел нацело и с остатком, четность и нечетность чисел, простые и составные числа, алгоритм Евклида, признаки делимости, НОД и НОК, взаимно простые числа и ММИ. .
. при делении на 3 может давать в остатке только 0 или 1. Число
при делении на 3 может давать в остатке только 0 или 1. Число  делится на 3 нацело, т.е. с остатком 0, значит, остаток левой части при делении на 3 может быть только 0 или 1, а число 8 делится на 3 с остатком 2. Следовательно, данное равенство при натуральных a иb не возможно.)
делится на 3 нацело, т.е. с остатком 0, значит, остаток левой части при делении на 3 может быть только 0 или 1, а число 8 делится на 3 с остатком 2. Следовательно, данное равенство при натуральных a иb не возможно.) делится на 7 тогда и только тогда, когда
делится на 7 тогда и только тогда, когда  делится на 7.
делится на 7. =10(
=10(  =7(
=7( 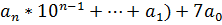 +3(
+3(  =7(
=7(  )+3
)+3  .Первое из 2ух слагаемых делится на 7; сумма будет делиться на 7 тогда и только тогда, когда и 2ое слагаемое будет делиться на 7. А это возможно тогда и только тогда, когда
.Первое из 2ух слагаемых делится на 7; сумма будет делиться на 7 тогда и только тогда, когда и 2ое слагаемое будет делиться на 7. А это возможно тогда и только тогда, когда 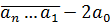 делится на 7.)
делится на 7.) –несократима ни при каком натуральном n.
–несократима ни при каком натуральном n. и
и  оканчиваются на 2,
оканчиваются на 2, 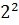 и
и  оканчиваются на 4.)
оканчиваются на 4.)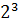 и
и  оканчиваются на 8 и т.д. Чему равна длинна цикла?
оканчиваются на 8 и т.д. Чему равна длинна цикла? .
. на 3.
на 3. делится на 6.
делится на 6. делится на 6. Значит, при n=1 утверждение истинно.
делится на 6. Значит, при n=1 утверждение истинно. . В полученной сумме первое слагаемое делится на 6 по предположению индукции, второе слагаемое делится на 6, т.к. произведение (k+1)k четное, и число 12 делится на 6. Т.к. каждое слагаемое делится на 6, то и вся сумма делится на 6. Значит, предполагая, что утверждение истинно для n=k,доказали, что оно истинно для n=k+1.)
. В полученной сумме первое слагаемое делится на 6 по предположению индукции, второе слагаемое делится на 6, т.к. произведение (k+1)k четное, и число 12 делится на 6. Т.к. каждое слагаемое делится на 6, то и вся сумма делится на 6. Значит, предполагая, что утверждение истинно для n=k,доказали, что оно истинно для n=k+1.) на 7
на 7 на 8 (стр. 48)
на 8 (стр. 48) на 7. (стр. 99)
на 7. (стр. 99) делится на 9. (стр. 103)
делится на 9. (стр. 103) .
.