
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Способ. Использование геометрического смысла модуля.Решить неравенство │х–2│< 3 Решение: Решениями неравенства будут числа, находящиеся на расстоянии меньше 3 от нуля модуля, равном 2.
Способ. Использование свойства модулей: модули противоположных чисел равны. Если │а│=2, то а = 2 или а = – 2 Способ: Использование определение модуля числа.
Определение:l а l= –а, если а<0. 3) Условие g(х) ≥ 0 является необходимым для существования решения уравнения │f(х)│= g (х). Но это не значит, что при условии g(х) ≥ 0 уравнение обязательно будет иметь корни. Например, решить уравнение: │2х + 1│= х2 + 2х +4 Решение: уравнение имеет решение, если х2 + 2х +4 = (х + 2)2 ≥ 0 при любых значениях х. Найдем корни уравнения: │2х + 1│= х2 + 2х +4
2х + 1 ≥ 0 2х – 1 < 0 2х + 1= х2 + 2х +4 – (2х + 1)= х2 + 2х +4
х2 + 3 = 0 х2 + 4х +5=0 нет корней
х2 = – 3 нет корней Ответ: коней нет. Способ: Решение неравенства на интервалах 1) Решить неравенство │х +1│+│х – 3│ ≤ 5 Решение: нули модуля: –1; 3.
а) х х
б) х
х
в) х х Итак: 
Методы решения 1)модуль меньше числа |f(x)|<=a
f(x)< –a 3)модуль меньше функции |f(x)|<g(x)
f(x)<g(x) f(x)> –g(x) 4)модуль больше функции |f(x)|>g(x)
f(x)< –g(x)
5.Уравнения. Равносильные уравнения. Уравнения–следствия. Уравнение – это математическое утверждение, записываемое в виде равенства двух буквенных выражений с переменными, которое истинно при одних значениях переменных и ложно при других их значениях. Решить уравнение – значит найти все значения переменных, при которых это утверждение превращается в верное числовое равенство, или доказать, что таких значений не существует. Уравнением с одним неизвестным (где Областью определения уравнения называется множество всех значений переменной Корнем (или решением) уравнения называется всякое число Замечание. Решение уравнения считается правильным только в том случае, если найдены все корни уравнения и в процессе решения убедительно доказано, что множество корней именно такое, как указанно в ответе. В частности, метод «угадывания» корней считается правильным, если доказано, что других корней нет. Уравнение вида называется уравнением с параметром Процесс решения уравнения – это последовательность некоторых преобразований, производимых над левой и правой частями уравнения и позволяющих заменить данное уравнение другим уравнением, решение которого известно или очевидно. Пусть в процессе решения уравнения Если преобразование уравнений может привести к потере корней, необходимо отдельно рассмотреть «выпадающие» в результате выполнения этого преобразования значения переменных, проверив их на принадлежность к множеству решений. Число Равносильными называются два уравнения Уравнения называются равносильными на некотором множестве Если все корни уравнения |
|||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 140. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Ответ: x є (–1;5)
Ответ: x є (–1;5) а , если а ≥ 0,
а , если а ≥ 0, 

 х ≥ –0,5
х ≥ –0,5 
 (–∞; –1) – (х +1) – (х – 3) ≤ 5 –х –1 –х +3 ≤ 5 –2х ≤ 3 х ≥ –1,5
(–∞; –1) – (х +1) – (х – 3) ≤ 5 –х –1 –х +3 ≤ 5 –2х ≤ 3 х ≥ –1,5
 [ –1; 3) х + 1 – (х –3) ≤ 5 х + 1 – х +3 ≤ 5 0*х ≤1 , х любое число
[ –1; 3) х + 1 – (х –3) ≤ 5 х + 1 – х +3 ≤ 5 0*х ≤1 , х любое число

 Ответ: х
Ответ: х  f(x)<=a
f(x)<=a f(x)>= –a
f(x)>= –a 2)модуль больше числа |f(x)|>a
2)модуль больше числа |f(x)|>a f(x)>a
f(x)>a g(x)>=0
g(x)>=0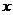 называется равенство
называется равенство 
 заданные функции), в котором требуется найти все значения
заданные функции), в котором требуется найти все значения 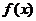 называется левой частью, а
называется левой частью, а  – правой частью уравнения. В частности, может быть
– правой частью уравнения. В частности, может быть  .
.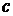 , при подстановке которого в уравнение получается верное числовое равенство
, при подстановке которого в уравнение получается верное числовое равенство  . Уравнение может иметь один, два, три и большее число корней, а также бесконечное их множество или не иметь корней вовсе.
. Уравнение может иметь один, два, три и большее число корней, а также бесконечное их множество или не иметь корней вовсе. , где
, где 
 , если ставиться задача для каждого значения параметра
, если ставиться задача для каждого значения параметра  . В общем случае каждый корень уравнения зависит от значения параметра:
. В общем случае каждый корень уравнения зависит от значения параметра:  .
. было получено уравнение
было получено уравнение  . Говорят, что при этом произошла потеря корней, если существует хотя бы одно число
. Говорят, что при этом произошла потеря корней, если существует хотя бы одно число 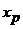 , которое является корнем исходного уравнения, но не является корнем уравнения
, которое является корнем исходного уравнения, но не является корнем уравнения  называется посторонним корнемуравнения
называется посторонним корнемуравнения  :
:  .
. значений неизвестной, входящем в области определения уравнений, если они имеют одни и те же решения, принадлежащие множеству
значений неизвестной, входящем в области определения уравнений, если они имеют одни и те же решения, принадлежащие множеству 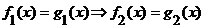 .
.