
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение дифференциальных уравненийЕсли на вход САР поступило возмущающее воздействие хвх(τ), то система начнет работать и переходить из одного состояния равновесия в другое. Изменение выходной величины вовремя этого перехода хвых(τ) называется переходным процессом. Переходный процесс может быть получен как решение дифференциального уравнения при известном хвх(τ) и заданных начальных условиях. Под начальными значениями понимается значение выходной величины и всех ее производных до (n-1)-ой в нулевой момент времени (n-1)-ую, равны нулю Методы решений дифференциальных уравнений с постоянными коэффициентами известны из курса высшей математики. Так решение уравнения (2.1.) находится как сумма двух составляющих – свободной и вынужденой: хвых(τ)=хвых.с.+хвых.в. [2.4] Вынужденная составляющая хвых.в является частным решением исходного дифференциального уравнения:
и определяется
где Ск – постоянная интегрирования; рк – вещественные корни характеристического уравнения аnpn+ an-1pn-1+…+a2p2+a1p1+a0=0 [2.7] Каждая пара сопряженных комплексных корней рк=αк 
Значения постоянных интегрирования определяются из начальных условий.
Передаточная функция
Если обозначить d/dt через р, то уравнение (2.1.) можно записать в символическом, так называемом операторном виде
или
где р – некоторое комплексное число, оператор. Отношение полинома В(р), характеризующего входную величину, к полиному А(р), характеризующего выходную величину, является передаточной функцией.
В знаменателе передаточной функции всегда стоит левая часть характеристического уравнения - характеристический полином. Строго говоря, передаточная функция получается из дифференциального уравнения после совершения над ним прямого преобразования Лапласа (одна из операций раздела высшей математики “Операционное исчисление”) при нулевых начальных значениях. При этом входная и выходная величины преобразуются в функции:
Видно, что передаточная функция полностью совпадает с выражением (2.10.), полученным из символической формы записи дифференциального уравнения (2.8.). Передаточная функция так же, как и дифференциальное уравнение, полностью характеризует динамику элемента и системы автоматического регулирования, но поскольку она не содержит производных, а является алгебраическим выражением, то существенно упрощает операции по получению динамических характеристик сложных систем, состоящих из различно соединенных элементов.
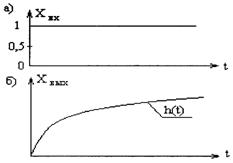
Переходная функция. При сравнении динамических свойств элементов и систем удобно рассматривать их реакции на некоторые типовые входные воздействия. Одним из таких типовых воздействий является единичная ступенчатая функция 1(τ) (рис 2.1).
Рис. 2.1 Переходная функция объектов управления: а – единичная ступенчатая функция 1(t); б – переходная функция h(t).
1(τ)= Переходный процесс в элементе или в системе после поступления единичного ступенчатого входного воздействия хвх(τ)=1(τ) называется переходной функцией и обозначается h(τ). Переходная функция h(τ) является решением дифференциального уравнения при нулевых начальных условиях и хвх=1, а также может быть найдена по формуле Хевисайда с использованием передаточной функции h(τ)=W(0)+ где рк – корни характеристического полинома уравнения А(р), стоящего в знаменателе передаточной функции (корни характеристического уравнения); В(рк) – значение числителя передаточной функции при р=рк; W(0) – значение передаточной функции при р=0; n – порядок дифференциального уравнения.
Практика 2
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 169. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  ,
,  …
… 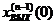 . При исследовании САР наиболее распространены нулевые начальные условия, когда выходная величина и все ее производные, включая
. При исследовании САР наиболее распространены нулевые начальные условия, когда выходная величина и все ее производные, включая [2.5]
[2.5] , [2.6]
, [2.6] jωк характеристического уравнения (1.13.) дает в решении (1.11.) составляющую вида
jωк характеристического уравнения (1.13.) дает в решении (1.11.) составляющую вида [2.8]
[2.8]
 [2.8]
[2.8] , [2.9]
, [2.9]

 [2.10]
[2.10] и
и  , называемые изображениями входной и выходной величин. Передаточной функцией W(p) называется отношение изображения выходной величины к изображению входной при нулевых начальных условиях:
, называемые изображениями входной и выходной величин. Передаточной функцией W(p) называется отношение изображения выходной величины к изображению входной при нулевых начальных условиях:
 [2.11]
[2.11] =
=  .
.
 (1.17.)
(1.17.) , (1.18.)
, (1.18.) - значение производной знаменателя передаточной функции при р=рк.
- значение производной знаменателя передаточной функции при р=рк.