
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальные уравнения с разделяющимися переменными.Дифференциальные уравнения с разделёнными переменными. ДУ с разделёнными переменными имеют вид: (*) M(x)dx + N(y)dy = 0, где M(x) и N(y) некоторые функции. Интегрируя ДУ (*), получаем общее решение в неявном виде: ∫M(x)dx +∫N(y)dy = C, где C∈R
Дифференциальные уравнения с разделяющимися переменными. ДУ с разделяющимися переменными имеют вид: M1(x)N1(y)dx +M2(x)N2(y)dy = 0, где M1(x), N1(y), M2(x) и N2(y) некоторые функции.
Оно может быть приведено к ДУ с разделёнными переменными путём деления обеих его частей на выражение N1(y)M2(x) ( где N1(y)≠0 и M2(x)≠0 )
Получили ДУ вида (*). И общим решением ДУ в неявном виде будет
УПРАЖНЕНИЯ: I.Решить ДУ (найти общие решения ДУ): 1.1) 1.2) 1.3) 1.4) II.Решить задачу Коши (найти частные решения ДУ, удовлетворяющие начальным условиям): 2.1) 2.2) 2.3)
1.1) Найти общее решение ДУ
Решение. Имеем ДУ с разделяющимися переменными. Необходимо переменные разделить. Поскольку
Полученное уравнение - ДУ с разделёнными переменными и теперь надо обе части этого уравнения проинтегрировать:

откуда
где произвольную постоянную C удобно записать в виде
Тогда,
откуда
следовательно,
Знаки
Ответ. Общее решение ДУ :
1.2) Найти общее решение ДУ DV
Решение. Данное уравнение- ДУ с разделяющимися переменными. Преобразуем его:
Получим
Проинтегрируем обе части этого уравнения:
1) Вычислим интеграл 2) Итак, (Для вычисления интеграла
откуда,
где произвольную постоянную C удобно записать в виде
Далее (по свойствам логарифма
откуда
следовательно,
Знаки
Тогда,
или
Ответ. Общее решение ДУ:
1.3) Найти общее решение ДУ
Решение. Это ДУ с разделяющимися переменными. Разделяем переменные:
1) Вычислим интеграл 2) Вычислим интеграл
откуда
где произвольную постоянную C удобно записать в виде
Далее
откуда
следовательно
Знаки Тогда,
Ответ. Общее решение ДУ:
1.4) Найти общее решение ДУ
Решение. Это ДУ с разделяющимися переменными. Разделяем переменные:
1) Вычислим интеграл 2) В правой части уравнения- табличный интеграл
Тогда получим
или
Ответ. Общее решение ДУ:
2.1) Найти частное решение ДУ
Решение. Это ДУ с разделяющимися переменными. Разделяем переменные:
1) 2) Вычислим интеграл
тогда
Полученное уравнение является общим решением данного ДУ. Для того, чтобы найти частное решение ДУ, найдём С, подставляя в общее решение ДУ начальные условия
Следовательно, частное решение ДУ:
Ответ: Частное решение ДУ 2.2) Решить задачу Коши:
Решение. Это ДУ с разделяющимися переменными. Разделяем переменные:
1) 2) Вычислим интеграл
Следовательно
Тогда получим
где произвольную постоянную C удобно записать в виде
Тогда
где произвольная постоянная
откуда
Это и есть общее решение ДУ. Для нахождения частного решения ДУ, найдём С, подставляя в общее решение ДУ начальные условия
Тогда
откуда
Следовательно, искомое частное решение ДУ
Откуда
Ответ: частное решение ДУ
2.3) Решить задачу Коши:
Решение. Это ДУ с разделяющимися переменными. Разделяем переменные:
1) Первый интеграл- табличный: 2) Вычислим интеграл Следовательно
получим
Найдем С: если
Следовательно
Ответ: Частное решение ДУ
|
|||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 130. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , тогда
, тогда  .
.  , где C∈R
, где C∈R Ответ:
Ответ: 
 Ответ:
Ответ: 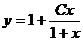
 Ответ:
Ответ: 
 Ответ:
Ответ:
 ,
,  Ответ:
Ответ: 
 ,
,  Ответ:
Ответ: 
 ,
, 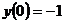 Ответ:
Ответ: 
 .
. , тогда запишем данное ДУ в виде:
, тогда запишем данное ДУ в виде:
 ∣
∣ 
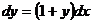 ∣
∣ 

 ,
, Вычислим интеграл
Вычислим интеграл  . Сделаем замену переменной
. Сделаем замену переменной  , тогда
, тогда 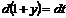 и
и  . Следовательно
. Следовательно 

 ,
, и где
и где  (по свойству логарифма
(по свойству логарифма  ).
). (по свойству логарифма
(по свойству логарифма  )
) ,
,
 можно опустить, так как наличие произвольной постоянной С их неявно учитывает. Тогда,
можно опустить, так как наличие произвольной постоянной С их неявно учитывает. Тогда, или
или  .
.

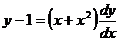 ∣
∣  ∣
∣  (разделяем переменные)
(разделяем переменные)
 .
.

 . Делаем замену переменной
. Делаем замену переменной  , тогда
, тогда  и
и 
 Вычислим интеграл
Вычислим интеграл  . Преобразуем подынтегральную функцию:
. Преобразуем подынтегральную функцию:  , откуда
, откуда  . Допуская
. Допуская  , получим
, получим  . Допуская
. Допуская  , получим
, получим  , откуда
, откуда  .
.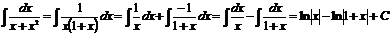
 используем метод подстановки
используем метод подстановки  или формулу
или формулу  )
)
 ,
,
 )
) ,
,


 .
. ∣
∣ 



 . Делаем замену переменной
. Делаем замену переменной  , тогда
, тогда  и
и  . Следовательно
. Следовательно 
 . Делаем замену переменной
. Делаем замену переменной  , тогда
, тогда  и
и  . Следовательно
. Следовательно 
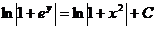

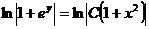 (по свойству логарифмов)
(по свойству логарифмов) ,
,
 .
. ∣
∣ 



 . Делаем замену переменной
. Делаем замену переменной  , тогда
, тогда  и
и  или
или 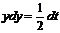 . Следовательно
. Следовательно 


 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 
 ∣
∣ 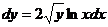 ∣
∣ 


 Вычислим интеграл
Вычислим интеграл  .
. 
 методом интегрирования по частям.
методом интегрирования по частям.  Пусть
Пусть  и
и  , тогда
, тогда  и
и  . Следовательно ,
. Следовательно , 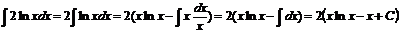
 ∣
∣ 

 и
и 
 или
или 
 , если
, если 
 ∣
∣  ∣
∣ 


 Вычислим интеграл
Вычислим интеграл  . Делаем замену переменной
. Делаем замену переменной  , тогда
, тогда  и
и  . Следовательно
. Следовательно 
 . Преобразуем подынтегральную функцию:
. Преобразуем подынтегральную функцию:  . Делаем замену переменной
. Делаем замену переменной  , тогда
, тогда и
и  .
.



 (по свойству логарифма)
(по свойству логарифма)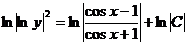 ,
, представлена в виде
представлена в виде  (по свойству логарифма)
(по свойству логарифма)
 и
и 

 , то есть
, то есть 
 или
или 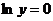
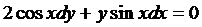 , если
, если 
 ∣
∣ 
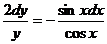



 . Делаем замену переменной
. Делаем замену переменной  и
и 

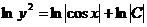

 -общее решение ДУ
-общее решение ДУ и
и 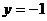 , тогда, подставляя эти начальные условия в общее решение ДУ, получим:
, тогда, подставляя эти начальные условия в общее решение ДУ, получим:
 то есть
то есть