
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Перечень вопросов выносимых на экзаменпо дисциплине «Сопротивление материалов» направление подготовки 14.05.02 «Атомные станции, проектирование, эксплуатация и инжиниринг »
1. Статический момент сечения относительно оси “Х”. а) 2. Осевой момент инерции прямоугольника с размерами B×h относительно центральной оси “у”. а) 3. Теорема о параллельном переносе осей для центробежного момента инерции сечения. а) JХУ=JХс–abF ; б) JХУ=JХсУс–abF ; в) JХУ=JХсУс+abF;
4. Определить центробежный момент инерции прямоугольника b×h относительно осей, проходящих через центр тяжести сечения. а) 5. Чему равен осевой момент инерции круга относительно оси, проходящей через его центр тяжести. а) 6. Осевой момент инерции сечения относительно оси “у”. а) 7.Чему равна сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей. а) Sx ; б) Jxy ; в) Jp 8. Как записывается теорема о параллельном переносе осей, если центральная ось “Хс”. а) JХ+JУ =JР ; б) JХc=JХ+a2F ; в) JХ =JХc+a2F 9. Что называется полярным моментом инерции сечения. а) 10. Осевой момент инерции квадрата с размерами (а × а) относительно центральной оси “Х”. а) 11. Связь между осевыми и полярными моментами инерции.  а) J х– Jy= Jp ; б) Jp = Jy – Jх ; в) Jp = Jх+Jy 12. Определить относительно какой оси: хс или ус момент инерции прямоугольника больше, если размеры прямоугольника b и h (h > b). а) х ; б) ус ; в) хс 13. Чему равен полярный момент инерции круга относительно его центра. а) 14. Какой знак имеют осевые моменты инерции сечения. а) отрицательный ; б) положительный ; в) равен нулю
15.Как изменится центробежный момент инерции при повороте осей координат на 90°? . а) JХ1У1= – JХУ ; б) JХУ=JХс–abF ; в) JХУ=JХcУс+abF 16. Осевой момент инерции кольца с размерами d×D относительно центральной оси “Х”. а) 17. Какой момент инерции может принимать отрицательные значения а) Jx ; б) Jxy ; в) Jp 18. Осевой момент инерции прямоугольника с размерами b×h относительно центральной оси “y”. а) 19. Центробежный момент инерции сечения в интегральной форме: а) 20. Измениться ли сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей при их повороте. а) нет; JУ1+ JХ1= JУ+ JХ ; б) да; JУ1+ JУ = JХ1 ; в) да; JУ1 – JУ = JХ1+ JХ 21. Чему равен статический момент сечения относительно оси, проходящей через центр тяжести сечения. а) Smax; б) Smin; в) S=0 22. Осевой момент инерции треугольника относительно оси Хс, если высота треугольника h, основания b. а) 23. Чему равен полярный момент инерции кольца относительно его центра. а) 24. Будет ли равен нулю центробежный момент инерции сечения, имеющего одну ось симметрии? а) нет ; б) да; в) не зависит 25. Чему равен центробежный момент инерции относительно главных осей инерции? а) JХУ >0; б) JХУ <0; в) JХУ =0 26. Чему равен осевой момент инерции прямоугольника, с размерами b×h, относительно оси абсцисс, проходящей через центр плоскости прямоугольника. а) 27. Осевой момент инерции сечения относительно оси “x”. а) 28. Чему равен полярный момент инерции круга относительно центра. а) 29.Растягиваемый стержень заменили другим с площадью поперечного сечения в два раза большей. В каком из вариантов напряжения останутся неизменными: а) силу уменьшили в 2 раза; б) силу увеличили в 2 раза; в) силу уменьшили в 4 раза. 30. По какой из формул определяется коэффициент запаса прочности для пластичного материала? а) 31. Какие напряжения нужно создавать в образце, чтобы при повторном нагружении у него был выше предел упругости? а) s > sт ; б) s = sт ; в) s < sт 32. Какие свойства материала характеризует коэффициент Пуассона? а) остаточные ; б) пластические ; в) упругие
33. Растягиваемый стержень заменили другим, тех же размеров, с модулем Юнга в два раза большим. В каком из вариантов относительное удлинение останется прежним: а) силу уменьшили в 2 раза; б) силу увеличили в 2 раза; в) силу увеличили в 4 раза; г) силу оставили неизменной; 34. По какой из формул находятся касательные напряжения в любом сечении сжатого стержня? а) 35. Как называется напряжение, при котором деформация образца происходит при постоянном растягивающем усилии? а) предел прочности; б) предел упругости; в) предел текучести. 36. Какой зависимостью связано полное напряжение с составляющими а) Р = 37. Два сжатых стержня, равные по размерам, имеют разную жёсткость (у I –го она больше). Различны ли их модули Юнга? а) нет. Е1<Е 2; б) да. Е1<Е 2; в) да. Е1 >Е2. 38. Условие прочности при растяжении – сжатии имеет вид: а) 39. Указать выражение, соответствующее жёсткости сечения при растяжении–сжатии. а) ЕI ; б) ЕF ; в) GF 40. Полная деформация образца состоит из: а) упругой и пластической; б) пластической; в) только упругой. 41. Как определить по диаграмме σ – ε модуль Юнга? а) 42. Условие жёсткости при растяжении – сжатии. а) 43. Какие напряжения возникают в поперечном сечении при центральном растяжении – сжатии? а) касательные; б) нормальные; в) t и s; 44. Как называется напряжение, до которого остаточная деформация при разгрузке не обнаруживается? а) предел прочности; б) предел упругости; в) предел текучести. 45. Произвели наклёп материала. Как изменились его свойства и характеристики? а) увеличился предел упругости и уменьшилась пластичность; б) увеличился предел упругости и увеличилась пластичность; в) ничего не изменилось. 46. По какой из приведённых формул определяются нормальные напряжения при растяжении: а) 47. Как называется напряжение, соответствующее максимальной силе? а) предел временного сопротивления; б) предел упругости; в) предел текучести. 48. Сколько внутренних силовых факторов возникает в поперечных сечениях прямого бруса при центральном растяжении (сжатии)? а) отсутствуют; б) два; в) один 49. Отношение относительной поперечной деформации к относительной продольной деформации называется: а) абсолютным удлинением; б) коэффициентом Пуассона; в) модулем упругости 50. Закон Гука при растяжении–сжатии имеет вид: а) 51. Для какого напряжения справедлив закон Гука? а) предел прочности; б) предел пропорциональности; в) предел текучести. 52. Если продольная сила N вызывает сжатие отсечённой части, то она считается: а) положительной; б) отрицательной 53. Величина коэффициента Пуассона колеблется в интервале: а) 0≤µ≤0,5; б) 0≥µ≥0,5; в) 0≤µ≤1
54. По какой из формул определяется коэффициент запаса прочности для хрупкого материала? а) 55. Разделив абсолютное удлинение стержня на его относительное удлинение, что мы получим: а) коэффициент Пуассона; б) модуль Юнга; в) первоначальную длину стержня. 56. Какие параметры характеризуют пластичность материала? а) относительное остаточное удлинение; б) относительное сужение площади сечения(Y); в) одновременно и Y и d 57.По какой из приведённых формул вычисляются нормальные напряжения при плоском изгибе в произвольной точке сечения. а) 58. Какой вид имеет закон Гука при изгибе? а) 59. Возникновением каких внутренних силовых факторов характеризуется прямой поперечный изгиб? а) М изг ; б) Q ; в) Мизг и Q
60. Первая производная от изгибающего момента по длине балки равна: а) поперечной силе ; б) интенсивности равномерно распределенной нагрузки ; в) изгибающему моменту.
61. Укажите, какая из приведённых величин является осевым моментом сопротивления а) 62. Формула проектного расчёта при изгибе? а) 63. Какие напряжения в поперечных сечениях балки изменяются по линейному закону по высоте сечения? а) τ ; б) σ ; в) τ и σ 64. Разделив изгибающий момент на осевой момент сопротивления, получим: а) нормальное напряжение; б) допускаемую силу ; в) момент инерции 65. По какой из приведённых формул определяются касательные напряжения при плоском поперечном изгибе. а) 66. Осевой момент сопротивления для прямоугольника с размерами b×h. а) Wx=bh³/32 ; б) Wx=bh³/12; в) Wx=bh²/6 67. Проинтегрировав уравнение а) уравнение углов поворота; б) кривизну балки ; в) уравнение прогибов
68. Какие напряжения достигают наибольших значений в области нейтральной оси. а) касательные ; б) нормальные; в) таких напряжений не существует
69. Условие прочности при изгибе имеет вид: а) 70. Формула определения максимальной допускаемой нагрузки при изгибе: а) [Mкр] ≤[τ] · Wp ; б) [Nmax]≤ [σ] · F; в) 71. Указать выражение, соответствующее жесткости сечения при изгибе. а) 72. Возникновением каких внутренних силовых факторов характеризуется прямой чистый изгиб а) Мизг ; б) Q ; в) Мизг и Q 73. По какой из формул определяется кривизна изогнутой оси бруса, характеризующая деформацию изгиба. а) 74. Формула определения максимальных касательных напряжений при изгибе для круглого сечения. а) 75. Какая связь между линейными и угловыми перемещениями при изгибе? а) y= 76 . Что такое упругая линия балки? а) кривизна нейтрального слоя ; б) нейтральная линия сечения; в) изогнутая ось балки 77. Чему равен осевой момент сопротивления круглого сечения? а) 78. Чему равны касательные напряжения при изгибе в крайних волокнах балки? а) 0; б) τmax; в) 79. По какой формуле определяются максимальные нормальные напряжения при изгибе. а) 80. Дифференциальные зависимости при изгибе между поперечной силой и изгибающим моментом. а) q= 81. Какие перемещения получают поперечные сечения балок при изгибе ? а) линейные ; б) угловые; в) линейные и угловые 82. Чему равны максимальные касательные напряжения при изгибе в прямоугольном поперечном сечении балки? а) 83. Осевой момент сопротивления квадрата со стороной а. а) Jx = 84 . Какое сечение более рационально использовать при одинаковых моментах сопротивления: круг, двутавр, квадрат. а) круг; б) двутавр; в) квадрат 85. Условие прочности при кручении имеет вид: а) 86. По какой из формул определяется коэффициент запаса прочности для хрупкого материала? а) 87. Стальной скручиваемый вал заменили таким же, но медным, как изменятся напряжения? а) не изменятся; б) увеличатся в два раза; в) уменьшатся в два раза
88. Указать выражение, соответствующее жёсткости сечения при кручении а)
89. Условие жесткости при кручении имеет вид: а) 90. Полярный момент инерции для сплошного круглого сечения определяется: а) 91. Крутящий момент увеличили в 16 раз. Как следует изменить диаметр вала, чтобы не изменился угол закручивания? а) увеличить в 3 раза; б) увеличить в два раза; в) уменьшить в два раза
92. Условие прочности при сдвиге: а) 93. По какой из приведенных формул определяются касательные напряжения в произвольной точке поперечного сечения а) 94. Какое из приведенных выражений соответствует полярному моменту сопротивления а) 95. Два вала одинаковой длины и диаметра, но из разных материалов (G2=2G1), закручивается на одинаковый угол. Каково отношение крутящих моментов m1:m2 а) 2; б) 0,25 ; 96. Закон Гука при кручении имеет вид: а) 97. Какой математической зависимостью связаны физические величины Е, а) G = 98. По какой формуле определяется коэффициент запаса прочности для пластичного материала? а) n = 99. Вычислить полярный момент инерции для круглого сечения диаметром d = 4см. а) JP = 256 см4 ; б) Jp = 2,51 см4 ; в) JP = 25,1 см4 100. Какое напряженное состояние возникает в каждой точке круглого бруса при кручении? а) чистый сдвиг; б) объёмное ; в) линейное 101. Какое из приведенных выражений будет соответствовать проектировочному расчету при кручении а) 102. Полярный момент инерции кольцевого поперечного сечения равен: а) 103. Крутящие моменты скручиваемых валов относятся , как Мкр1 : Мкр2 = 1 : 8. Как относятся их диаметры, если а) d1: d2 = 1:3 ; б) d1: d2 = 4:1; в) d1: d2 = 1:2 104. Каким количеством констант можно охарактеризовать упругое поведение материала? а) 2; б) 3; в) 1 105. Закон Гука при сдвиге имеет вид: а) 106. Какое из приведенных выражений будет соответствовать проверочному расчету при кручении а) МКР 107. Два вала одинаковой длины и диаметра, но из разных материалов (G2 = 2G1), скручиваются одинаковыми моментами. Каково отношение углов закручивания а) 0,5 ; б) 2; в) 0,25 108. От какой геометрической характеристики сечения при кручении зависит жесткость бруса? а) JP; б) Wp; в) F 109. Как вычисляется по заданной мощности (в кВт) к числу оборотов (об/мин) момент, передаваемый шкивом? а) Мк = 7028 110. Какой формулой надо воспользоваться для вычисления момента сопротивления круглого сечения? а) 111. Как по диаграмме а) 112. От какой геометрической характеристики сечения при кручении зависит прочность бруса? а) JP; б) Wp; в) F
Составил: Ст.преподаватель Л.Н. Пичугова Зав.кафедрой «Механика и материаловедение» к.т.н., доцент Э.М. Таратин
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 214. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
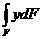 ; б)
; б) 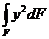 ; в)
; в) 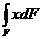
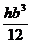 ; б)
; б) 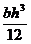 ; в)
; в) 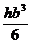
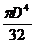 ; б)
; б) 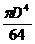 ; в)
; в) 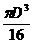
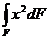 ; б)
; б) 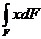
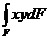 ; б)
; б) 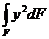 ; в)
; в) 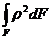
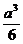 ; б)
; б) 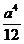 ; в)
; в) 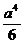
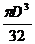 ; б)
; б) 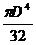 ; в)
; в) 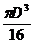
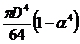 ; б)
; б) 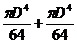 ; в)
; в) 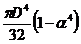
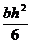 ; б)
; б) 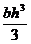 ; б)
; б) 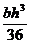
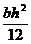 ; б)
; б) 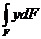 ; б)
; б) 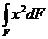
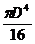 ; б)
; б) 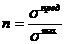 ; б)
; б) 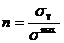 ; в)
; в) 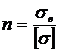
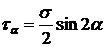 ; б)
; б) 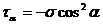 ; в)
; в) 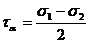
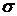 и
и  ?
?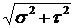 ; б) Р =
; б) Р =  ; в) Р =
; в) Р = 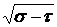
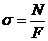 ; б)
; б) 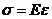 ; в)
; в) 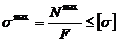 ;
;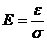 ; б) tg α ; в) sin α
; б) tg α ; в) sin α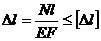 ; б)
; б) 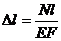 ; в)
; в) 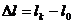 .
.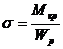 ; в)
; в) 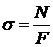 .
.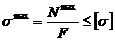
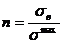 ;
;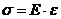 ; б)
; б) 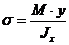 ; в)
; в) 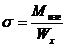
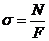 ; б)
; б) 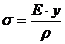 ; в)
; в) 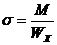
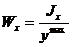 ; б)
; б) 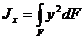 ; в)
; в) 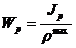
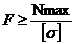 ; б)
; б) 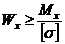 ; в)
; в) 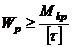
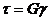 ; б)
; б) 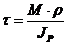 ; в)
; в) 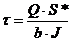
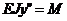 дважды, получим:
дважды, получим: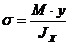 ; б)
; б) 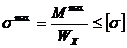 ; в)
; в) 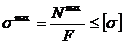
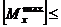 [σ] · Wx
[σ] · Wx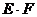 ; б)
; б) 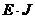 ; в)
; в) 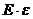
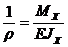 ; в)
; в) 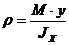
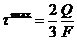 ; б)
; б) 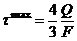 ; в)
; в) 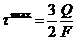
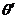 ; б)
; б) 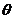 =
= 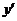 ; в) y=
; в) y= 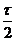
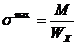 ; б)
; б) 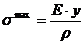 ; в)
; в) 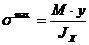
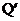 ; б) M=
; б) M= 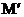
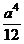 ; б) Jx =
; б) Jx = 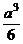 ; в) Jx =
; в) Jx = 
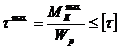
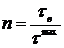 ; в)
; в) 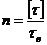 ;
;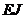 ; б) GF ; в) GJp
; б) GF ; в) GJp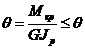 ; б)
; б) 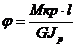 ; в)
; в) 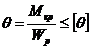
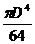 ; б)
; б) 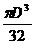 ; в)
; в) 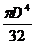
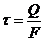 ; б)
; б) 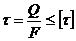 ; в)
; в) 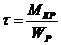 ;
;  б)
б) 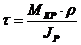 ; в)
; в) 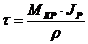
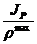 ; б)
; б)  ; в)
; в) 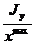
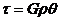 ; б)
; б) 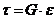 ; в)
; в) 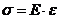
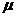 ,G?
,G?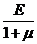 ; б) G =
; б) G = 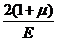 ; в) G =
; в) G = 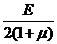
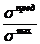 ; б) n =
; б) n = 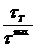 ; в) n =
; в) n = 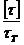
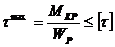 ; б) M
; б) M 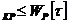 ; в) W
; в) W 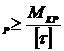
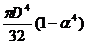 ; б)
; б) 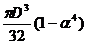 ; в)
; в) 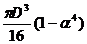
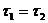
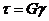 ; б)
; б) 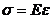 ; в)
; в) 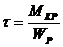
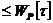 ; б)
; б) 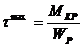
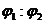 ?
?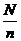 ; б) Мк = 9549
; б) Мк = 9549 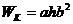 ; б)
; б) 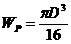 ; в)
; в) 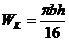
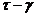 определить модуль сдвига G:
определить модуль сдвига G: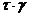 ; б) tg α; в) sin α
; б) tg α; в) sin α