
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теория измерений применительно к информационно-измерительным приборам и системамОсновные моменты теории измерений Измерение Измерение - это организованное действие человека, выполняемое для количественного познания свойств физического объекта с помощью определения опытным путем значения какой-либо физической величины [3] или же измерение - совокупность операций, выполняемых с помощью специвльных средств для определения количественного значения величины [4] Измерение является важнейшим понятием в метрологии. Основные понятия зафиксированы в Статье 2 Федерального закона РФ 102-ФЗ "Об обеспечении единства измерений" [4] Прежде чем рассматривать непосредственно методы измерений, остановимся на понятии «измерение» в общем смысле слова. Измерение – это процесс сравнения двух величин и выражение результата измерения цифрой, имеющей размерность. Обязательными компонентами любого измерения являются: 1) физическая величина, значение которой нужно измерить; 2) единица физической величины; 3) метод измерения; 4) средство измерения (техническое средство, предназначенное для измерений [4]); 5) наблюдатель (ЭВМ); 6) условия окружающей среды; 7) результат измерения. B метрологии по способу получения результатов принято различать следующие виды измерений [5, Шивринский Проектирование…2009] : - прямые, - косвенные - совокупные - совместные Данная классификация важна в особенности потому, что каждая категория измерений связана с определенным способом обработки экспериментальных данных для нахождения результата измерения и оценивания его погрешностей. Прямое измерение - измерение, при котором искомое значение величины получают непосредственно от средства измерений [4]  При прямых измерениях процесс измерения производится над самой измеряемой величиной, которую сравнивают с мерой непосредственно или же с помощью измерительных приборов, градуированных в требуемых единицах. Примерами прямых служат измерения длины тела линейкой, массы при помощи весов и др. Прямые измерения широко применяются в машиностроении, а также при контроле технологических процессов (измерение давления, температуры и др.). Косвенные - это измерения, при которых искомую величину определяют расчетным путем на основании прямых измерений других величин, связанных с измеряемой известной зависимостью, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Например, Примеры косвенных измерений: определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения. Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить непосредственно или когда прямое измерение дает менее точный результат. Роль их особенно велика при измерении величин, недоступных непосредственному экспериментальному сравнению, например размеров астрономического или внутриатомного порядка. Совокупные - это производимые одновременно измерения нескольких одноименных величин, при которых искомую определяют решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Примером совокупных измерений является определение массы отдельных гирь набора (калибровка по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь). Совместные - это производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимостей между ними. В качестве примера можно назвать измерение электрического сопротивления при 200С и температурных коэффициентов измерительного резистора по данным прямых измерений его сопротивления при различных температурах. Также измерения делят на статические и динамические. Обычно к статическим измерениям будем относить измерения, при которых в соответствии с поставленной задачей средства измерений применяются в статическом режиме; к динамическим — при которых они применяются в динамическом режиме. При этом под статическим режимом средства измерений следует понимать режим, при котором выходной сигнал применительно к назначению средства измерений можно считать неизменным. Например, для показывающего прибора — неизменным в течение времени, достаточного для отсчитывания его показания. Под динамическим режимом будем понимать режим, при котором выходной сигнал изменяется во времени так, что для получения результата измерения или для оценивания его точности необходимо это изменение учитывать. Согласно этим определениям, к статическим измерениям, кроме тривиальных измерений длины, массы и т.п., относятся также измерения показывающими приборами средних и действующих (средних квадратических) величин переменного тока. К динамическим измерениям относятся измерения последовательных значений величины, изменяющейся во времени (в том числе стохастически). Типичным примером подобных измерений является запись (регистрация) изменения величины во времени. В этом случае логично считать, что производится не одно, а множество измерений. К статическим измерениям нужно относить и измерения, выполняемые с помощью показывающих цифровых приборов. В соответствии с определением статических измерений для такого заключения не имеет значения то, что при измерении в самом приборе изменяется состояние элементов (триггеров, реле и т. п.). Измерение останется статическим и тогда, когда показания прибора время от времени будут изменяться, но каждое показание будет сохраняться в течение времени, достаточного для его отсчитывания или автоматической регистрации. Характерным признаком динамических измерений является то, что для получения результатов и оценивания их точности при этих измерениях необходимо знать одну из полных динамических характеристик средств измерений: дифференциальное уравнение, передаточную функцию и т. д. Погрешность измерения Правильность измерения определяется как качество измерения, отражающее близость к нулю систематических погрешностей результатов (т.е. таких погрешностей, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины). Важнейшей характеристикой качества измерений является их достоверность; она характеризует доверие к результатам измерений и делит их на две категории: достоверные и недостоверные, в зависимости от того, известны или неизвестны вероятностные характеристики их отклонений от истинных значений соответствующих величин. Результаты измерений, достоверность которых неизвестна, не представляют ценности и в ряде случаев могут служить источником дезинформации. Позитивной характеристикой измерений является их точность. Под точностью измерений понимается качество измерений, отражающее близость их результатов к истинному значению измеряемой величины. Соответственно, погрешности измерений характеризуют несовершенство измерений, и могут считаться негативными характеристиками измерений. Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой величины [6]. Измерение тем более точно, чем меньше его погрешность. В результате сравнения (сличения) измеряемой физической величины с истинным значением По форме выражения погрешностей измерений различают погрешности абсолютные и относительные. Абсолютная погрешность измерения – это погрешность, выраженная в единицах измеряемой величины, для математического описания которой используется выражение 1.1:
Однако приведенное соотношение нельзя использовать для нахождения погрешности измерения по той простой причине, что истинное значение измеряемой величины всегда неизвестно; если же его можно считать известным, то измерение не нужно. Поэтому погрешности измерений приходится оценивать с использованием косвенных данных. Абсолютные погрешности в общем случае зависят от значения измеряемой величины и поэтому не годятся для количественной характеристики точности измерений. Этого недостатка не имеют относительные погрешности. Относительная погрешность измерения – это погрешность, выраженная в долях истинного значения измеряемой величины:
Поэтому точность количественно можно охарактеризовать числом, равным обратному значению относительной погрешности, выраженной в долях измеряемой величины. Обязательными компонентами всякого измерения являются метод измерения и средства измерений; очень часто измерения выполняются с участием человека. Несовершенство каждого компонента измерения вносит вклад в погрешность измерения, поэтому в общем виде погрешность записывается следующим выражением:
где
Каждая из составляющих погрешности измерения в свою очередь может вызываться рядом причин. Так, методические погрешности могут возникать вследствие недостаточной разработанности теории тех явлений, которые положены в основу измерения, и неточности тех соотношений, которые используются для нахождения оценки измеряемой величины. В частности, погрешность вследствие порогового несоответствия модели конкретного объекта самому объекту является также методической погрешностью. Инструментальные погрешности измерения – погрешности из-за несовершенства средств измерений. Обычно различают основную погрешность средств измерений – погрешность в условиях, принятых за нормальные, и дополнительные погрешности, т.е. погрешности, обусловленные отклонением влияющих величин от их нормальных значений. Личные погрешности. Обычно измерения выполняются людьми. Человек отсчитывает показания приборов, фиксирует момент исчезновения изображения нити накаливания на экране оптического пирометра и т. д. Индивидуальные особенности лица, выполняющего измерения, обусловливают появление индивидуальных, свойственных данному лицу погрешностей. К ним относят погрешности из-за неправильного отсчитывания десятых долей деления шкалы прибора, асимметричной установки штриха оптического индикатора между двумя рисками и т. п. Совершенствование конструкций отсчетных и регулировочных устройств средств измерений привело к тому, что при применении современных средств измерений личные погрешности обычно незначительны. Как описывалось выше, наличие погрешности ограничивает достоверность измерений, т.е. вносит ограничение в число достоверных значащих цифр числового значения измеряемой величины и определяет точность измерений. Поэтому основной задачей является нахождение величины абсолютной погрешности для последующего учета данного значения. По точности оценивания погрешностей применяют следующую классификацию измерений. Измерения с точным оцениванием погрешностей – измерения, при которых учитывают индивидуальные свойства средств измерений и контролируют условия измерений. Измерения с приближенным оцениванием погрешностей – измерения, при которых учитывают нормативные данные о свойствах средств измерений и приближенно оценивают условия измерений; наиболее существенные влияющие величины иногда измеряют. Измерения с предварительным оцениванием погрешностей – измерения, при которых регламентированы типы (марки) применяемых средств измерений, условия выполнения измерений и заранее оценены погрешности. Заметим, что измерения с предварительным оцениванием погрешностей часто называют техническими измерениями. Приведенная классификация относится, естественно и к обыкновенным, и к статистическим, и к статическим, и к динамическим. Теория измерений применительно к информационно-измерительным приборам и системам Решение задач получения информации и контроля параметров технических объектов в процессе эксплуатации, а также при проведении научных исследований и экспериментов неразрывно связано с использованием различных измерительных приборов, систем и комплексов, являющихся средствами получения количественной информации о контролируемом объекте или процессе. Информация – мера неоднородности распределения материй и энергии в пространстве и во времени. Она характеризует изменения, которые свойственны процессам и явлениям. Измерительная информация (соответственно, информация, получаемая в процессе измерения) – количественная оценка состояния материального объекта, полученная экспериментально, путем сравнения параметров объекта с мерой (эталоном). Тогда, с позиций теории информации, под точностью измерительного прибора или системы подразумевается возможность обеспечить в выходном сигнале необходимое количество измерительной информации о действительном значении входного сигнала. При определении количества информации в выходном сигнале прибора или системы все точностные характеристики необходимо приводить к единому объективно обоснованному показателю – эквивалентному числу делений, ступеней, квантов в рабочем диапазоне входного сигнала, названному П. В. Новицким «информационной способностью измерительного устройства» [9, 10]. Носителем измерительной информации является энергия или вещество. Без получения энергии (прямого или косвенного) от источника информации, собственно, невозможно измерительное преобразование. Погрешности измерительных приборов и систем в процессе измерения характеризуются потерей информации при ее восприятии, преобразовании, передаче и воспроизведении. Соответственно, чем меньше потери информации, тем меньше погрешности и, следовательно, тем лучше прибор или система. И, наоборот, при увеличении погрешности измерительного прибора (системы) уменьшается количество измерительной информации, измеряемой прибором (системой). Для оценки информационных характеристик измерительных приборов и систем используют понятия: количества информации (единицей количества информации является бит), информационной производительности и пропускной способности [8]. Однако процесс получения и преобразования измерительной информации сопровождается действием случайных возмущений и помех и вносимой ими дезинформацией в процессе измерения. В общем случае возмущающие входные сигналы и воздействия (помехи и шумы) измерительных приборов являются случайными, поэтому при одних и тех же условиях погрешности приборов и систем имеют различные размеры. Особенностью таких случайных величин является то, что практически ничего нельзя сказать об их повелении в будущем, даже если известен характер поведения в прошлом [5.22]. Например, если взять несколько однотипных гироскопических датчиков угловой скорости, запустить их на неподвижном основании и записывать их выходные сигналы, начиная с некоторого момента времени. Так как основание неподвижно (вращением Земли не учитывается), то записи будут представлять собой погрешности (шумы) выходных сигналов гироскопов. Несмотря на то, что гироскопы однотипные, их погрешности будут принимать разные значения в разные моменты времени в силу всевозможных причин: неидентичности геометрических параметров конструкции, систем возбуждения и съема сигнала; различия установки и многих других неконтролируемых факторов. Все это приведет к тому, что после записи будет получена картина, приведенная на рис.1.1.
Примерно такая же картина будет получена, если записывать шум одного гироскопа и затем совместить записанные интервалы. Значение каждой конкретной записи в определенный момент времени Случайным процессом (функцией) называется такая функция, значение которой при каждом фиксированном значении времени является случайной величиной. Сечением случайного процесса называются значения случайного процесса в некоторый фиксированный момент времени. Так, значения погрешностей гироскопов в момент времени Размер случайных погрешностей можно оценить с использованием подходов, разработанных в теории вероятностей [***]. Для описания случайных процессов вводятся вероятностные характеристики, аналогичные случайным величинам. В отличие от числовых характеристик случайных величин, характеристики случайных процессов в общем случае - неслучайные функции времени [Распопов, Матвеев]. В основу теории случайных процессов (функций) положено пять неслучайных функций, характеризующих процесс: 1) математическое ожидание случайного процесса - характеризует поведение процесса в среднем; 2) дисперсия случайного процесса - характеризует рассеивание значении процесса во времени относительно среднего значения; 3) корреляционная функция - характеризует степень линейной зависимости между двумя сечениями случайного процесса; 4) спектральная плотность дает спектральное представление случайного процесса. 5) плотность распределения - дает представление о распределении случайного процесса в фиксированные моменты времени; Случайная погрешность
Интегральная функция распределения отражает значение вероятности появления размера погрешности не больше некоторой текущей величины
Дифференциальная функция распределения
Вероятность P распределения погрешности
Законы распределения случайной погрешности Δx характеризуют некоторыми численными значениями – неслучайными статистическими моментами. Первый центральный момент или математическое ожидание погрешности
Математическое ожидание, т.е. «средняя» неслучайная функция времени
Отклонение случайной погрешности от математического ожидания определяют вторым центральным моментом – дисперсией
Следовательно, дисперсия случайного процесса Чтобы иметь характеристику разброса случайного процесса в его размерности, вводится среднеквадратическое отклонение
Среднеквадратическое отклонение (СКО) есть арифметическое значение квадратного корня из дисперсии случайного процесса:
Важнейшим дополнением моментов первого и второго порядков является центральный момент второго порядка для двумерного закона распределения, учитывающего зависимость погрешности от времени
где
Свойство эргодичности стационарных случайных погрешностей позволяет определить математическое ожидание, дисперсию и корреляционную функцию по ограниченному числу реализаций или по одной реализации путем осреднения погрешностей и их характеристик на достаточно большом периоде времени Т. Для этого используются следующие выражения:
где
При анализе случайных погрешностей чаще всего в практике инженерных расчетов используют нормальную и равномерную плотности распределения. Если выполнится предположение о том, что погрешности измерения могут принимать непрерывный ряд значений, то при большом числе измерений частота появления погрешностей, равных по абсолютной величине, но различного знака – одинакова и малые погрешности встречаются чаще, чем большие. Поэтому для описания случайных погрешностей следует применять нормальный (Гауссовский) закон распределения вероятностей
где
На рис. 2.3 показаны кривые изменения плотности вероятностей f(Δx) при различных значениях σΔx= σi.
Рис. 2.3. Графики изменения плотности вероятностей случайной погрешности Из графиков на рис. 2.3 видно, что при малых значениях σi вероятнее получить малую погрешность измерений, чем большую. Вероятность того, что погрешность измерения находится между заданными значениями Δx1 и Δx2, вычисляется по формуле
В табл. 2.1 приведены значения вероятностей для интервалов [Δx1; Δx2], заданных в единицах Таблица 2.1
Значение погрешности, равной 2/3 σΔx называют вероятной погрешностью, а значение 3σΔx часто считают наибольшей возможной (предельной) погрешностью. Однако при большом числе измерений (n>20÷30) максимальная погрешность нередко может превышать 3σΔx.
В общем случае случайные погрешности Δy на выходе измерительных приборов и систем зависят от значения измеряемой величины x и характеризуются условными законами распределения, которые могут быть представлены в виде: а) условной функции распределения F(Δy/x), выражающей условную вероятность появления случайной погрешности в интервале от - ∞ до Δy при данном значении x; б) условной плотности распределения, являющейся производной условной функции распределения
Геометрически условная плотность распределения изображается кривой, форма которой зависит от характера распределения (рис. 2.4, а). Условная вероятность попадания случайной погрешности Δy в поле допусков
где Δyн и Δyв – нижняя и верхняя границы поля допусков на величину Δy при данном значении x. На рис. 2.4, а эта вероятность выражается заштрихованной площадью.
а) б) Рис. 2.4. Условная плотность распределения случайной погрешности (а) и плотность распределения системы случайных величин x и Δy (б).
Для перехода от условного распределения к безусловному следует рассматривать систему двух случайных величин, одной из которых является измеряемая величина x, другой – погрешность Δy. Система двух случайных величин (x, Δy) геометрически интерпретируется как случайная точка на плоскости x, Δy или как случайный вектор, составляющими которого являются случайные величины x и Δy. Плотность распределения системы x, Δy связана с условной плотностью распределения Δy формулой
где f1(x) – безусловная плотность распределения x (распределение x не зависит от Δy). Геометрически плотность распределения системы g(x, Δy) изображаются поверхностью (рис. 2.4, б). Величина f1(x) выражается площадью сечения функции g(x, Δy) плоскостью, проходящей через точку x перпендикулярно к оси x (см. заштрихованную площадь на рис. 2.4, б), а условная плотность f(Δy/x) равна ординате кривой, огибающей это сечение, деленной на площадь сечения.
2.3. Квантильные оценки случайных погрешностей измерительных приборов и систем
Если построить кривую плотности распределения f(Δx) случайной погрешности Δx измерительного прибора или системы (рис. 2.5), то согласно правила нормирования площадь под кривой равна единице, т. е. отражает вероятность всех возможных событий.
Рис. 2.5. Доверительные вероятности и доверительные интервалы случайных погрешностей
Эту площадь под кривой можно разделить на некоторые части вертикальными линиями. Абсциссы таких линий называются квантилями. Так Δx= Δx1 есть 5% - ная квантиль, так как площадь слева от нее составляет 5% всей площади, а справа 95% . Соответственно значения Δx2, Δx3, Δx4 и Δx5 на рис. 2.5 будут 10% - ная, 50% - ная, 90% - ная и 95% - ная квантили. Интервал значений погрешности Δx между Δx1= Δx0,05 и Δx5= Δx0,95 охватывает 90% всех возможных значений случайной погрешности и называется интерквантильным промежутком d0,9 с 90% - ной доверительной вероятностью. Его протяженность d0,9= Δx0,95 - Δx0,05. Интерквантильный промежуток d0,8= Δx0,9 - Δx0,1 и включает в себя 80% всех возможных значений случайной погрешности Δx. На основании такого подхода вводится понятие квантильных оценок случайной погрешности, т. е. значений погрешности с заданной доверительной вероятностью Pд как границу отрезка ± Δxд=± dд/2, на протяжении которого встречается Pд процентов всех значений случайной погрешности, а (1–Pд) процентов общего числа возможных значений погрешности оказывается за границами этого интервала. Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами доверительной вероятности Pд и соответствующим доверительным интервалом ± Δxд. Полученная оценка случайной погрешности есть указание "максимального" значения погрешности Δxд с заданной доверительной вероятностью Pд. Для нормирования случайной и результирующей погрешности средств измерений используются значения доверительных вероятностей Pд=0,9 и Pд=0,95. Достоинство доверительной погрешности состоит в том, что ее значение может быть оценено по экспериментальным данным. При проведении некоторого ряда измерений можно определить среднее арифметическое значение измеряемой величины Доверительная вероятность Pд есть вероятность того, что При небольшом числе измерений (n<20), результаты измерений подчиняются нормальному закону распределения и поэтому для определения погрешности с заданной доверительной вероятностью Pд целесообразно использовать распределение Стьюдента. В табл. 2.2. приведены так называемые квантили распределения Стьюдента |
Квантили распределения Стьюдента Таблица 2.2.
Чтобы найти доверительный интервал ± Δxд, необходимо для данных n и Pд найти квантиль |
где σср – среднее значение средней квадратической погрешности σΔx ряда измерений. Среднее квадратическое значение погрешности n измерений определяется
где xi – результат i-го измерения. Тогда среднее значение σср определяется как
При этом следует иметь в виду, что по ограниченным экспериментальным данным не могут быть получены точные доверительные значения случайной погрешности, а только лишь приближенные значения – оценки. Поэтому квантильные оценки с большими доверительными вероятностями могут быть найдены только при большом числе измерений. Число измерений n, необходимо для определения Δxд с заданной вероятностью Pд определяется соотношением
где nотб – число результатов измерений из общего числа n, которые имеют наибольшие по модулю отклонения xi от среднеарифметического значения Для различных значений Pд и nотб необходимое число измерений n приведено в табл. 2.3 [10].
Таблица 2.3
Основным недостатком оценки случайной погрешности доверительным значением Δхд при произвольно выбираемом Pд является невозможность суммирования доверительных значений случайной погрешности с разными доверительными вероятностями. Анализируя дезинформационные действия случайных помех с различными законами распределения вероятностей К. Шеннон пришел к выводу [9], что вносимая помехой ξ дезинформация определяется не только мощностью этой помехи, т. е. ее среднеквадратическим значением σξ, но еще зависит от вида закона распределения этой помехи. Если помеха ξ статистически не зависит от сигнала x, то аддитивное действие помехи на сигнал может быть определен ее энтропией, т. е. интегральной функцией, определяющей средневзвешенную меру дезинформации, дополнительной неопределенности выходного сигнала измерительного прибора (системы)
Предположим, что измеряемый случайный процесс характеризуется величиной x, принимающей n дискретных значений x1, x2, …, xn с вероятностями P(x1), P(x2), …, P(xn). Пусть величина x измеряется прибором с дискретным выходом y, причем y принимает значения y1, y2, … , yn с вероятностями P(y1), P(y2), … , P(yn). Величины x и y являются, вообще говоря, зависимыми, поэтому их совместная вероятность будет P(xi, yk). Средним количеством информации относительно измеренного значения y, заключенного в измеряемом процессе x, называется величина Отсюда следует, что среднее количество информации положительно или равно нулю, т. е. J(x, y)≥0. Случай J(x, y)=0 будет при P(xi, yk)= P(xi) P(yk), т. е. для независимых величин x и y. Но это будет тогда, когда погрешность измерения равна самой измеряемой величине. Если x=y (погрешности отсутствуют), то J(x, x)=J(y, y)=∞. (1.27) Следовательно, 0 ≤ J(x, y) ≤ ∞. В случае непрерывных процессов, описываемых векторами x (x1, x2, …, xn) и y(y1, y2, …, yn), количество информации процесса x, измеряемого прибором с выходом y, определяется по формуле J(x, y) =∫∫ p(x, y) log2 [P(x, y)/ p(x) p(y)]dx dy, (1.28)
где p(x), p(y), p(x, y) – плотности распределения вероятностей. Если воспользоваться тем, что p(x, y)= py (x) p(y)= p(x) px (y), то выражению (1.27) можно придать вид J(x, y)=H(x) - My[Hy(x)]= H(y) - Mx[Hx(y)], (1.29) где Mx, My – знаки математического ожидания; Hx, Hy – меры неопределенности сигналов x и y, называемые энтропией, которые связаны с плотностями распределения вероятностей соотношениями
При получении измерительной информации энтропия уменьшается, поэтому энтропию можно трактовать как недостаточную информацию о сигнале. В выражении (1.29) члены H(x) и H(y) дают информацию, которую можно было бы получить с помощью прибора без погрешностей. Величины My[Hy(x)] и Mx[Hx(y)] определяется погрешностями прибора.
Литература 1. Основы проектирования измерительных приборов и систем: Учебное пособие / В.М. Солдаткин, А.А. Порунов, В.В. Солдаткин; Казань: Изд-во Казан. гос. техн. ун-та, 2004. 337с 2. Рецензенты: д.т.н., проф. Ципенко В.Г., д.т.н., проф. Калугин В.Т. Ефимова М.Г. Основы авиации. Часть 2. Конструкция и основные функциональные системы летательных аппаратов: Учебное пособие. – М.: МГТУГА, 2005. 52 с., 1 табл., 32 ил., лит.: 5 наим. 3. Тюрин Н.И. Введение в метрологию. М.: Изд-во стандартов, 1985. 4. Федеральный закон Российской Федерации от 26 июня 2008 г. N 102-ФЗ "Об обеспечении единства измерений" 5. ГОСТ 16263-70 6. Рабинович С. Г. Погрешность измерений. – Л.: Энергия. 1978, - 262 с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 173. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 получают ее оценку (результат измерения)
получают ее оценку (результат измерения)  . Иными словами, погрешность измерения
. Иными словами, погрешность измерения  есть разность между
есть разность между 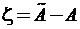 ,
где
,
где 

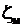 - погрешность методическая;
- погрешность методическая; - погрешность инструментальная;
- погрешность инструментальная; - погрешность личная.
- погрешность личная.
 будет представлять случайную величину (эти значения отмечены точками на рис. 1.1). Таким образом, случайная величина, меняющаяся со временем, представляет собой случайный процесс.
будет представлять случайную величину (эти значения отмечены точками на рис. 1.1). Таким образом, случайная величина, меняющаяся со временем, представляет собой случайный процесс. наиболее полно характеризуется именно функцией (плотностью) распределения вероятности: дифференциальной
наиболее полно характеризуется именно функцией (плотностью) распределения вероятности: дифференциальной  или интегральной
или интегральной  , связанных между собой соотношениями 1.4:
, связанных между собой соотношениями 1.4:
 . Это неубывающая функция случайной погрешности
. Это неубывающая функция случайной погрешности  .
.

 и
и  , определяется интегрированием плотности вероятности
, определяется интегрированием плотности вероятности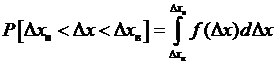
 определяется для непрерывной функции распределения зависимостью 1.6:
определяется для непрерывной функции распределения зависимостью 1.6:
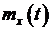 , вокруг которой происходит разброс реализаций случайного процесса (рис. 1.4) является важнейшей характеристикой случайного процесса
, вокруг которой происходит разброс реализаций случайного процесса (рис. 1.4) является важнейшей характеристикой случайного процесса
 и его математическое ожидание
и его математическое ожидание  :
:
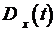 характеризует как бы мощность, степень разброса реализаций около его математического ожидания
характеризует как бы мощность, степень разброса реализаций около его математического ожидания 

 , который называют корреляционной функцией
, который называют корреляционной функцией
 ,
,  – реализация случайной погрешности в момент времени
– реализация случайной погрешности в момент времени  и
и  ;
; и
и  – реализация плотности распределения погрешности в момент времени
– реализация плотности распределения погрешности в момент времени 

 – среднеквадратическое значение случайной погрешности.
– среднеквадратическое значение случайной погрешности.

 [9].
[9].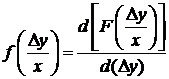




 , которая является оценкой истинного значения измеряемой величины xи. Значение измеряемой величины
, которая является оценкой истинного значения измеряемой величины xи. Значение измеряемой величины  как правило не совпадает с истинным ее значением, а отклоняется от него на величину погрешности Δx =
как правило не совпадает с истинным ее значением, а отклоняется от него на величину погрешности Δx =  (n)|Pд при заданной доверительной вероятности Pд=0,8÷0,99 для числа измерений n=2-30 [9].
(n)|Pд при заданной доверительной вероятности Pд=0,8÷0,99 для числа измерений n=2-30 [9].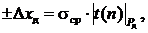 (2.32)
(2.32) (2.33)
(2.33) (2.34)
(2.34)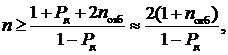 (2.35)
(2.35) (1.26)
(1.26)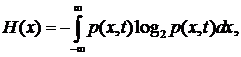 (1.30)
(1.30)