
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
II. Статистические группировки.I. Сводка статистических данных. В результате статистического наблюдения получают статистическую информацию, представляющую большое количество первичных разрозненных сведений об отдельных единицах объекта исследования. Поэтому необходимо для дальнейшего социально-экономического анализа привести эти материалы в порядок – систематизировать. Это достигается в результате сводки. Сводка – это научно организованная обработка и систематизация первичного статистического материала в целях выявления типичных черт и закономерностей развития изучаемых явлений. Задачи сводки: 1. Систематизация и группировка цифровых данных. 2. Характеристика образованных групп системой показателей. 3. Подсчет соответствующих итогов и представление результатов в виде таблиц и графиков. Инструменты систематизации информации: 1. Классификации. 2. Номенклатуры. 3. Группировки. Классификация – это систематизированное распределение явлений и объектов на определенные секции, группы, классы, позиции и виды на основании какого-либо признака (критерия) или нескольких признаков (критериев). Основой классификации служат классификаторы, представляющие собой систематизированный перечень объектов (отраслей, предприятий, продукции, занятий, основных фондов и т.п.), каждому их которых присваивается код. Пример: 1) Международная стандартная отраслевая классификация всех видов экономической деятельности – МСОК. Она разделяет экономическую деятельность на 17 секций, 159 групп, образующих 290 классов. 2) Общероссийский классификатор видов экономической деятельности, продукции и услуг – ОКДП. Он имеет 6 уровней классификации: раздел, подраздел, группа, подгруппа, класс, подкласс. В него входит 55 тыс. видов продукции и услуг по всем отраслям экономики.  Для установления принадлежности явлений и объектов к определённым классам и группам классификатор дополняется номенклатурой –т.е. стандартным перечнем объектов и их групп. Пример: Товарная номенклатура внешнеэкономической деятельности. В России существует Единая система классификации и кодирования информации – ЕСКК. Она обеспечивает взаимосвязь объектов, которые описываются в различных классификаторах. В свою очередь наибольшая часть общероссийских классификаторов базируется на действующих международных классификаторах.
II. Статистические группировки. В сводке статистического материала все объекты и единицы статистической совокупности объединяются в группы при помощи метода группировок. Статистическая группировка – это метод разделения множества единиц изучаемой совокупности на однородные по существенным признакам группы. Пример: 1) Группировка промышленных предприятий по формам собственности. 2) Группировка населения по среднедушевому доходу. 3) Группировка коммерческих банков по сумме активов баланса. С помощью метода группировки решаются следующие задачи: 1. выявление социально-экономических типов явлений; 2. изучение состава явления (его структуры); 3. выявление связи и зависимости между отдельными признаками общественных явлений. Классификация группировок. 1. В зависимости от решаемых задач. 1) Типологические. Разделяют качественно однородные совокупности на классы, социально-экономические типы, однородные группы. Пример: 1) Группировка населения по уровню образования. 2) Группировка предприятий по формам собственности. Таблица 1. Группировка промышленных предприятий региона по формам собственности.
Вывод: Подавляющее большинство предприятий находится в федеральной собственности, менее 5% составляют предприятия с частной формой собственности и только 1,5% - с муниципальной и смешанной собственностью. 2. Структурные. Группировки, разделяющие однородные совокупности на группы, характеризующие их структуру по какому-либо количественному признаку. Пример: 1) Группировка хозяйств по объему продукции. 2) Группировка предприятий по стоимости ОПФ. 3) Группировка населения по размеру среднедушевого дохода. Таблица 2. Группировка населения России по размеру среднедушевого дохода (1998).
Вывод: Данные показывают, что более 43% населения имело среднедушевой доход от 80 до 160 руб. в месяц, доход до 80 руб. получало 17% населения. 3. Аналитические (факторные). Группировки, выявляющие взаимосвязи между изучаемыми признаками. В этих группировках выделяют факторные -Х и результативные - У признаки. Факторными являются признаки, под воздействием которых изменяются результативные признаки. В основе построения данных группировок лежит факторный признак и каждая выделенная группа (по факторному признаку) характеризуется соответствующими значениями результативного признака. Пример: 1) Группировка рабочих по квалификации (факторный признак) с указанием их среднемесячной зарплаты (результативный признак). С помощью ее можно выявить зависимость уровня зарплаты рабочих от их квалификации. 2) Группировка предприятий по техническому уровню (факторный признак) с указанием производительности труда на предприятии (результативный признак). С ее помощью можно выявить зависимость производительности труда от технической оснащенности предприятий. 3) Группировка банков по сумме их активов с указанием средней численности занятых и суммы балансовой прибыли. Таблица 3 Группировка коммерческих банков России по сумме активов баланса.
Вывод: Данные таблицы показывают, что чем больше сумма активов, тем выше прибыль банка и численность его сотрудников. У первой группы средняя численность занятых в 2,8 раза меньше, чем у пятой, а балансовая прибыль меньше в 9,1 раз. 4. Многомерные группировки. Используются для анализа влияния множества факторных признаков, действующих в различных направлениях, на изменение величины результативного признака. При её построении абсолютные значения результативного признака (уi) заменяются отношениями: Qi = уi /
n – число результативных признаков. Абсолютные значения факторных признаков (хij) заменяются отношениями: Рij = хij /
n – количество факторных признаков i - го вида; В результате этой замены получается матрица отношений:
Если связь между результативным и факторным признаком обратная, то для каждой единицы определяется величина: 1 / Рij . На основе отношений Рij определяется показатель:
k – число факторных признаков. Данная величина покажет взаимосвязь между множеством факторных признаков и результативным. 2. В зависимости от числа признаков 1) Простые группировки. Группировки, в которых группы образованы по одному признаку. Пример: таблицы 1 и 2.
2) Сложные группировки (комбинированные). Группировки, в которых разделение на группы производится по двум и более признакам, взятым в сочетании. В данных группировках сначала группы формируются по одному признаку, затем они делятся на подгруппы по другому признаку, которые в свою очередь могут подразделяться по третьему и т.д. Пример: А) Дополнив простую группировку населения по возрастным группам, группировкой по полу получим сложную группировку. Б) Группировку рабочих по стажу работы можно дополнить подгруппами рабочих в зависимости от классности.
III. Ряды распределения. Ряд распределения – это упорядоченное распределение единиц совокупности на группы по определенному признаку. В зависимости от признака положенного в основу образования ряда выделяют: 1. Атрибутивные ряды распределения. Ряды, построенные по качественным признакам. 2. Вариационные ряды распределения. Ряды, построенные по количественному признаку. Вариация – это количественное различие признака внутри изучаемой совокупности. Состав вариационных рядов: а) варианты – это отдельные значения признака в ряду; б) частоты – это численности отдельных вариант или группы вариационного ряда, показывающие, как часто встречаются одинаковые варианты в ряду. Сумма всех частот определяет численность всей совокупности. Частоты, выраженные в долях единицы или в % к итогу называются частостями. Сумма частостей равна 1 ил 100%. Вариационные ряды подразделяют на: 1) Дискретные (прерывные). Ряды, где варианты имеют значения целых чисел. 2) Интервальные (непрерывные). Ряды, где признак может принимать любые значения в определённых пределах (интервалах), а варианты признака представлены в виде интервалов (от – до). 3) Ранжированные. Ряды, где значения признака (варианты) расположены в порядке возрастания или убывания их количественных значений. Графическое изображение рядов распределения дает наглядное представление о характере изменения частот вариационного ряда (форме распределения). Выделяют следующие графические изображения этих рядов: 1. Полигон. Используется для изображения дискретных вариационных рядов. Для его построения по оси абсцисс (х) откладываются ранжированные значения признака, а по оси ординат (у) – величины частот. Пример: Таблица 4 Распределение жилого фонда района по типу квартир.
Рис. 1. Полигон распределения жилого фонда района по типу квартир. 2. Гистограмма. Применяется для изображения интервальных вариационных рядов. При ее построении по оси х откладываются величины интервалов признака, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота частот пропорциональна частотам. Пример: Таблица 5. Распределение семей по размеру жилой площади приходящейся на 1 человека.
3. Кумулята. С её помощью изображается ряд накопленных частот. Накопленные частоты – это частоты показывающие, сколько единиц совокупности имеют значения признака не выше рассматриваемого значения. При её построении по оси хоткладываются варианты ряда, а по осиу – накопленные частоты (таблица 5).
Рис. 3. Кумулята распределения семей по размеру жилой площади, приходящейся на 1 человека.
Изображение ряда в виде кумуляты эффективно для рядов, частоты которых выражены частостями.
4. Огива. Если при графическом изображении ряда в виде кумуляты оси поменять местами, то получится огива.
IV. Правила построения статистических группировок. Построение группировок включает несколько этапов: 1. Изучение явления и выбор группировочного признака. В качестве данного признака берется факторный признак. 2. Определение числа групп и величины интервала. 2.1. Если признак качественный, то число групп будет соответствовать числу качественных вариант. 2.2. Если признак количественный, то необходимо: 2.2.1. Построить ранжированный ряд группировочного признака. 2.2.2 Построить графическое изображение ранжированного ряда На основе графического изображения оценивается интенсивность изменения группировочного признака.
е р . л и . и з
и а . н к .
. . единицы
На этом этапе возможно провести выделение групп. А) Если группировочный признак изменяется плавно, то для определения числа групп можно использовать формулу: n = 1 + 3,322 х lg N, где n – число групп данной группировки; N – число единиц совокупности. Тогда величина интервала определяется: X max – Xmin
n X max – максимальное значение признака; X min – минимальное значение признака. Б) Если группировочный признак изменяется резко или имеет значительный размах между минимальным и максимальным значением, то строятся неравные интервалы. Они могут быть прогрессивно возрастающими или убывающими в: 1) Арифметической прогрессии. В этом случае величина интервала определяется: h i + 1 = hi + a , где a – число на которое последующий интервал больше предыдущего. 2) Геометрической прогрессии. В этом случае величина интервала будет определяться: h i + 1 = hi х q , где q – число, показывающее во сколько раз последующий интервал больше предыдущего. В) Многие группировки в экономике строятся с произвольными интервалами, различными по своей величине, в зависимости от решаемых задач. 3. Построение интервального ряда распределения. 4. Выбор показателей для характеристики групп и построение вспомогательной таблицы для их расчета. 5. Построение итоговой группировочной таблицы, в которой определяется средний уровень для характеристики групп. 6. Анализ полученных данных.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 231. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 , где
, где  у – среднее значение результативного признака;
у – среднее значение результативного признака; , где
, где 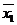
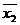


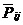 = Σ Рij / k , где
= Σ Рij / k , где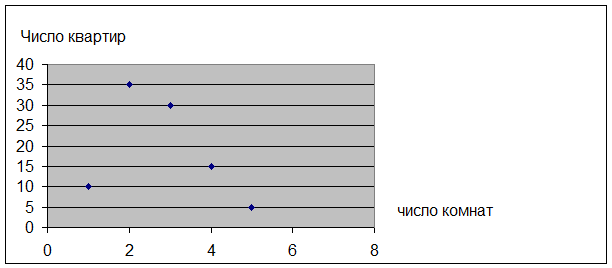



 В п .
В п . ч н .
ч н . 
 а а .
а а . I группа II группа III группа признака
I группа II группа III группа признака h = , где
h = , где