
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основні теоретичні положення дО виконання лабораторних робітМіністерство освіти і науки, молоді та спорту України Державний ВНЗ «Національний гірничий університет» МОДЕЛЮВАННЯ В МЕНЕДЖМЕНТІ ЛАБОРАТОРНИЙ ПРАКТИКУМ для студентів денної форми навчання освітньо-кваліфікаційного рівня бакалавр, напряму підготовки … «Менеджмент»
Дніпропетровськ Двнз «нгу» 2012 Моделювання в менеджменті: лабораторний практикум для студентів денної форми навчання освітньо-кваліфікаційного рівня бакалавр, напряму підготовки … «Менеджмент» / Державний ВНЗ «Національний гірничий університет»; І.Є. Лозинський, В.М. Шликова, С.П. Олійник – Д.: Державний внз «нгу», 2012. – .. с.
Укладач: І. Є. Лозинський В.М. Шликова С.П. Олійник
Рецензент: д.е.н., проф. В.Я. Швець
Рекомендовано кафедрою менеджменту виробничої сфери, протокол № .. від … 2012 р.
ЗМІСТ

Вступ
Математичне моделювання є перспективним та ефективним напрямом методології економічних досліджень. Використовуючи методи економіко-математичного моделювання можливо досліджувати економічні явища не лише у статиці, а й у динаміці. Сучасні методи моделювання роблять можливими науково-обґрунтоване прогнозування економічних явищ та процесів, аналіз стану виробничо-економічних систем та, відповідно, прийняття високоефективних управлінських рішень. Для студентів Державного ВНЗ «Національний гірничий університет», що навчаються за напрямком 0502 «Менеджмент», на третьому курсі обов'язковою для вивчення є дисципліна «Моделювання в менеджменті». Загальний час на засвоєння дисципліни складає 126 годин. Даний лабораторний практикум створено для набуття практичних навиків моделювання економічних процесів студентами курсу на лабораторних заняттях з дисципліни, а також для закріплення теоретичного лекційного матеріалу.
Організаційні вказівки До виконання лабораторних робіт
Лабораторні роботи виконуються за наступною програмою:
Перед виконанням лабораторної роботи студент повинен відновити теоретичні знання з відповідної теми за допомогою розділу «Основні теоретичні положення до виконання лабораторних робіт» даного лабораторного практикуму. Методичні вказівки по кожній з лабораторних робіт складаються з трьох розділів:
Лабораторні роботи виконуються студентом самостійно за консультаціями викладача та повинні бути представлені на перевірку та захищені відповідно до графіка, що оголошується на початку вивчення дисципліни. Захист робіт полягає у відповідях на запитання стосовно порядку виконання розрахунків та економічного змісту отриманих результатів. Оцінка за лабораторний модуль визначається як середня з відповідних оцінок за кожну окрему лабораторну роботу. Кожна окрема лабораторна робота оцінюється за такими критеріями:
Лабораторні роботи повинні бути оформлені (написані або роздруковані) на аркушах формату А4 з одного боку акуратно, без виправлень із дотриманням вимог стандарту ДСТУ 3008-95. «Документація. Звіти у сфері науки і техніки. Структура і правила оформлення». На початку роботи слід вказати прізвище, назву групи та варіант. Висновки за результатами моделювання повинні бути написані вручну. Основні теоретичні положення дО виконання лабораторних робіт
Традиційно, основою діяльності менеджера є здатність приймати ефективні та обґрунтовані рішення. Зазвичай такі рішення приймаються у результаті збору і накопичення емпіричних спостережень та даних, виявлення окремих закономірностей, побудови та аналізу створених моделей, що дає відповіді на різноманітні питання із широкого спектру управлінських ситуацій. Кожен висококваліфікований менеджер повинен вміти, за необхідності, не лише шукати серед існуючих моделей найбільш придатні до застосування, а й моделювати реальні життєві ситуації, створювати власні моделі. Для цього він має знати й уміти використовувати у будь-яких специфічних умовах повсякденної ділової практики базові методи кількісного моделювання. Процес моделювання умовно розділяють на три етапи: - Вивчення середовища з метою чіткої постановки проблеми; - Формалізація уявлення про ситуацію; - Побудова кількісної моделі. Оптимізаційні моделі.Якщо необхідно максимізувати (прибуток продуктивність) або мінімізувати (витрати, час) визначений критерій ефективності, який залежить від факторів, на які може впливати (які може корегувати) сам менеджер та які у свою чергу, підпорядковуються ряду обмежень, то така модель є типовим прикладом задачі умовної оптимізації. Обмеження у моделі завжди звужують діапазон можливих рішень, а тому умовна оптимізація – це досягнення найкращого можливого результату за наявності існуючих обмежень. Це той напрямок науки управління, який сьогодні найбільш активно розвивається. Методи лінійної оптимізації у сфері оптимізаційних моделей є основним і найбільш широко використовуваним інструментом. Моделі лінійного програмування використовуються як у найпростіших випадках з кількома десятками обмежень, так і у надскладних ситуаціях, які містять десятки тисяч змінних рішень і обмежень. Моделі лінійного програмування є одним з прикладів моделей умовної оптимізації. Задача лінійного програмування є математичною моделлю, що має наступні властивості: - цільова функція є лінійною (відсутні експоненти та комбінаційні складові); - обмеження (нерівності або рівності) також є лінійними функціями. Особливим класом задач лінійного програмування є транспортні задачі. Транспортні моделі можна назвати найбільш популярними серед моделей лінійного програмування. У подібних моделях здебільшого ставляться задачі організації постачання продукції, яка зберігається на складах, територіально розміщених по-різному, споживачам з найменшими витратами і, безумовно, дотримуючись усіх поставлених вимог. Транспортна модель – це модель лінійного програмування яка дозволяє знайти найдешевший спосіб задоволення попиту в а пунктах призначення при здійсненні постачань з b відправних пунктів. Метою транспортної задачі може бути не лише мінімізація цільової функції (витрат на транспортування вантажу), а й максимізація. Для цього необхідно скорегувати формулу цільової функції: коефіцієнтами її мають бути не питомі витрати а питомий прибуток. Якщо у транспортній моделі попит на досліджувану групу товарів дорівнює їх пропозиції, то така модель є збалансованою. У такому випадку для формалізації обмежень можна замість нерівностей використовувати рівності (оскільки у такій моделі попит та пропозиція збалансовані, то обмеження-нерівності в точці оптимальності стануть лімітуючими, тобто перетворяться у рівності). Транспортні моделі можуть бути також і незбалансованими: попит менший від пропозиції, або попит більший від пропозиції. У випадку коли попит менший за пропозицію особливих проблем з вирішенням задачі не виникне, оскільки надлишкова пропозиція товарів після задоволення всього попиту залишається у пунктах відправлення, тобто у резерві. А щодо формалізації вищевикладеного, то такий результат досягається внаслідок використання нерівностей у обмеженнях. Дещо складнішою є ситуація коли попит перевищує пропозицію. Тоді максимум, що може зробити підприємство – це задовольнити існуючий попит при найменших витратах. Є два шляхи вирішення. Обмеження для пропозиції можна формалізувати у вигляді рівностей, що примусить відправні пункти відправити увесь наявний товар у пункти призначення, а обмеження для попиту – у вигляді нерівностей «менше-дорівнює». Незадоволений попит у такому разі залишиться у вигляді резерву. Іншим способом є введення фіктивного відправного пункту, запас товару у якому точно відповідає різниці між загальним попитом та пропозицією. такий фіктивний відправний пункт робить модель збалансованою, коли попит дорівнює пропозиції. Вартість доставки з такого пункту у будь-який пункт призначення дорівнює нулю. Кожна поставка з такого пункту інтерпретується як незадоволений попит. Різновидом моделей лінійної оптимізації, а саме транспортної моделі, є моделі призначень, які дозволяють досліджувати розподіл фіксованих ресурсів, наприклад, оптимально розподілити наявних продавців по відділах магазину, чи завдання по станках. Модель призначень – це модель лінійного програмування яка дозволяє вирішити задачу знаходження оптимального розподілу а неподільних об’єктів на b завдань. Прикладами можуть бути розподіл продавців по відділах магазину, робітників по цехах підприємства, лікарів по викликах, призначення консультантів для клієнтів і т.д. Об’єкти які розподіляються є неділимими і тому не можуть бути зайнятими на декількох завданнях. Модель призначень є різновидом транспортної моделі. Вона відрізняється лише тим, що один об’єкт постачання не може розподілятися по декількох пунктах призначення. У моделі призначення усі значення попиту і пропозиції дорівнюють одиниці і, оскільки ми знаємо, що у транспортній моделі при цілих значеннях попиту і пропозиції оптимальне значення також буде цілим, то можна стверджувати, що оптимальне рішення задачі призначень також буде цілим числом. Виділяють також динамічні моделі, за допомогою яких приймаються скоординовані рішення на декілька часових періодів. Моделі, які розробляються для одного часового періоду називаються статичними моделями, а моделі, які охоплюють декілька часових періодів називаються динамічними моделями. Такі моделі, безумовно набагато точніше відображають реальність, адже часто рішення приймаються у залежності від часу, або від інших рішень, які були прийняті раніше. Звичайно, динамічні моделі є набагато складнішими за статичні. При їх створенні необхідно приділяти увагу набагато більшій кількості деталей. Зазвичай кожен часовий періо має власний критерій ефективності, але для оптимізації необхідно об’єднати ці критерії ефективності в єдиний критерій, який відображуватиме загальну ефективність за усі часові періоди. У якості такого критерію, як правило, використовується сума усіх критеріїв ефективності для окремих періодів, або найчастіше використовують зважену суму, де вагові коефіцієнти залежать від часу. Також необхідно прискіпливо визначити синхронізацію подій, щоб проміжні результати і рішення йшли у правильному порядку. Динамічні моделі управління запасами (багатофазові моделі управління запасами) – важливий клас моделей, які застосовуються для управління запасами матеріалів фінансів, трудових ресурсів і т.п. при переході від одного періоду до іншого. Транспортні моделі і моделі призначень є окремими випадками так званих сітьових моделей, загальною ознакою яких є вивчення переміщення або розподілу фізичних елементів (персоналу, продукції, фінансів і.т.п.). Вони використовуються здебільшого для оптимізації перевезень вантажів, знаходження найкоротшого шляху, або максимізації потоку у мережі. як правило, за допомогою сітьового підходу описуються досить масштабні ситуації. Діаграма потоків (сітьова діаграма) складається з комплексу вузлів та дуг, кожній з яких відповідає окрема пропускна здатність та питомі витрати (вартість перевезення вантажу через неї). Вузол пропозиції – вузол з додатнім значенням пропозиції, ще називаються джерелами або точками пропозиції Вузол попиту – вузол з від’ємним значенням пропозиції, ще називаються пунктами призначення, стоками або точками попиту. Вузол перевалки – проміжний вузол, що не є ні вузлом пропозиції, ні вузлом попиту Маршрут, або шлях між двома вузлами – це довільна послідовність дуг, що з’єднує ці вузли. Правило: якщо в моделі перевезень вантажів усі праві частини обмежень і пропускні здатності задані цілими числами, то існує цілочисельне оптимальне рішення даної задачі. Задача знаходження найкоротшого шляху виникає в такій діаграмі потоків, у якій кожна дуга означає відстань, або вартість, або час руху від попереднього до наступного вузла, які необхідно мінімізувати, що й інтерпретується як визначення найкоротшого (найдешевшого, найшвидшого) маршруту. Маршрутміж двома вузлами – це довільна послідовність дуг, що з’єднує ці вузли. У задачі знаходження найкоротшого шляху дуги ненаправлені, що означає можливість руху по кожній з них у обох напрямках, хоча у окремих випадках допустиме формування однонаправлених дуг (вулиця з одностороннім рухом). Моделі цілочисельного лінійного програмування (ЦЛП) – це окремий підвид моделей лінійного програмування, що містять додаткову вимогу щоб деякі або усі змінні рішення приймали цілі значення. Існує декілька класів моделей даної категорії: модель повністю цілочисельного лінійного програмування (модель, у якій усі змінні рішення повинні приймати тільки цілі значення) та модель частково-цілочисельного лінійного програмування (модель, у якій тільки деякі змінні рішення повинні приймати цілі значення, а усі інші можуть бути будь-якими).
Лабораторна робота №1 «МОДЕЛЮВАННЯ ЗА ДОПОМОГОЮ ЕЛЕКТРОННИХ ТАБЛИЦЬ EXCEL»
Мета роботи: набуття навичок та вмінь щодо використання засобів Excel для моделювання ситуації та її аналізу.
Завдання. Підприємці-початківці прийняли рішення зайнятися вендингом і зібралися орендувати визначену кількість (табл. 1) снекових торговельних автоматів SAECO Break Point 56 для продажу мінеральної води у приміщеннях замовників, університетах, на вокзалах, у торгівельних центрах та на вулицях міста. Окрім плати за аренду та інших витрат на автомати, підприємці думають про те, щоб здійснювати додаткову плату клієнтам-організаціям, які надають місце для установки автоматів у своїх приміщеннях. Таким чином, оплата за використання автоматів складатиметься зі щомісячної фіксованої плати за аренду місця під автомат плюс можливі деякі заохочувальні виплати. Таблиця 1 Кількість та основні характеристики продажів орендованих вендинг-автоматів
Довідка: останнім часом в Україні поширеним стає так званий вендинг. Це назва бізнесу, який означає торгівлю без фізичної участі людини і де для отримання кінцевого результату використовується автомат. Вендинг-бізнес розпочати досить просто: варто купити торговий автомат, знайти місце під його установку, заправляти його матеріалом, що витрачається і знімати виручку. Заробітком є різниця між собівартістю товару та його продажною ціною. Отже, чим більше продажів, тим більший прибуток.
У межах свого бізнес-плану молоді підприємці визначили рівень інших необхідних параметрів. Таблиця 2 Показники, необхідні для аналізу прибутковості нового підприємства
Для визначення оптимального варіанту було вирішено вивчити альтернативні варіанти структури орендної плати за виділене місце для установки торговельного апарату. Отже, окрім фіксованої щомісячної орендної плати (500 грн) за один торговельний автомат можна спробувати запропонувати клієнтам більш низьку орендну плату плюс визначені комісійні виплати з кожної проданої пляшки води. Наприклад, клієнти можуть отримувати за надання місця для установки торговельного апарату фіксовану орендну плату у розмірі 200 грн плюс 0,1 грн з кожної проданої пляшки або орендна плата може складати 100 грн, а комісійні з кожної пляшки, проданої зверх встановленого ліміту у 1000 шт становитимуть 0,15 грн. Необхідно: - порівняти обсяги щомісячного прибутку для трьох альтернативних варіантів структури орендної плати; - порівняти обсяги продажів, які відповідають точці беззбитковості для усіх трьох варіантів; - знайти точки байдужості у яких чистий прибуток не залежить від вибору альтернативного варіанту.
Порядок виконання роботи. 2.1. Створити файл Microsoft Excel. 2.2. Скопіювати вихідні дані 2.3. Для аналізу прибутковості нового підприємства розробити модель на базі електронних таблиць Excel (надати назви усіх стовпців та рядків моделі; для усіх величин вказати одиниці виміру; для розрахунку усіх формул використовувати посилання на комірки у яких містяться параметри, а не їх числові значення). Для цього сформувати допоміжні розрахункові таблиці середніх витрат на один вендинг-автомат та середнього місячного чистого доходу. 2.3.1. Формуємо таблицю середніх витрат на один вендинг-автомат (табл. 3). Таблиця 3 Середні витрати на один автомат на місяць
Пояснення: постійні витрати на один автомат складаються з суми витрат на оренду автомату, витрат на обслуговування та інших витрат.
Рекомендація: основною вхідною змінною моделі є кількість пляшок що продається за місяць 1 автоматом. Основний показник ефективності моделі – чистий щомісячний дохід від реалізації товару.
2.3.2. Формуємо таблицю середнього місячного чистого доходу (табл. 4). Таблиця 4 Середній дохід на місяць
Пояснення: дохід є добутком кількості наявних автоматів, кількості проданих пляшок і ціни однієї пляшки; вартість проданого товару є добутком кількості наявних автоматів, кількості проданих пляшок і змінних витрат на одну пляшку; валова вартість – різниця між доходом і вартістю товару; загальні та адміністративні витрати – добуток кількості автоматів і суми постійних витрат на утримання одного автомату та плати за оренду місця для нього; чистий дохід – різниця між валовою вартістю товару та загальними і адміністративними витратами. 2.4. Заповнити таблиці вихідними даними та визначити відсутні показники. 2.5. Підготувати таблицю для обчислення чистого доходу від реалізації проекту для трьох альтернативних варіантів (табл. 5) Таблиця 5 Порівняльна таблиця для трьох запропонованих варіантів структури орендної плати
Пояснення: комісійні витрати у випадку відсутності встановленого ліміту продажів дорівнюють добутку комісійних витрат на одну пляшку, кількості проданих пляшок та кількості наявних торгівельних автоматів. Комісійні витрати у випадку наявності встановленого ліміту продажів (за умови, що ліміт є меншим за кількість проданих пляшок) дорівнюють добутку комісійних витрат на одну пляшку, кількості автоматів та різниці між кількістю проданих пляшок та встановленим лімітом (у випадку, коли встановлений ліміт продажу – вищий за продану кількість пляшок, комісійні не нараховуються). Валова вартість проданого товару дорівнює різниці між доход від продажів та сумою вартості проданого товару і комісійних витрат. Загальні та адміністративні витрати є добутком кількості автоматів і суми постійних витрат на утримання одного автомату та плати за оренду місця для нього. Чистий дохід – різниця між валовою вартістю товару та загальними і адміністративними витратами відповідного варіанту. 2.6. Визначити точки беззбитковості (кількість проданих пляшок води, при якій різниця між валовою вартістю продукції та загальними і адміністративними витратами дорівнюватиме нулю, тобто кількість проданих пляшок води, при якій чистий прибуток буде нульовим) для усіх трьох варіантів за допомогою засобу Excel Підбір параметра. 2.7. Визначити точки байдужості (кількість проданих пляшок води, при якій чистий прибуток буде одинаковим для усіх альтернатив) для усіх трьох варіантів за допомогою засобу Excel Підбір параметра. 2.8. Порівняти параметри альтернативних варіантів та обрати оптимальний, обґрунтувавши прийняте рішення. Рекомендація: комірка, значення якої буде змінюватиметься (кількість проданих пляшок), повинна містити не посилання, а значення 2.9. За результатами моделювання зробити висновки.
Вимоги до оформлення звіту Звіт повинен містити: - вихідні дані; - розрахункові обчислення, виконані у роботі; - висновки, написані вручну.
Лабораторна робота №2 «ФОРМАЛІЗАЦІЯ І РОЗРАХУНОК ПАРАМЕТРІВ ТРАНСПОРТНОЇ МОДЕЛІ»
Мета роботи: набуття навичок та вмінь щодо формалізації та розрахунку параметрів збалансованих та незбалансованих транспортних моделей за умови мінімізації цільової функції.
Завдання Підприємство має 10 заводів по випуску однотипної продукції. З урахуванням розміщення на території країни споживачів, конфігурація дистрибуційної мережі, яка складається з 7 магазинів роздрібної торгівлі, має дещо іншу локалізацію. Виробничий план на листопад 2012 року уже сформований. Замовлення магазинів роздрібної торгівлі до заводів щодо необхідної кількості продукції на листопад (попит) представлено у табл. 1. Таблиця 1
У табл. 2 наведені обсяги продукції, які може виготовити для постачання у магазини роздрібної торгівлі (пропозиція) кожен із заводів. Таблиця 2
Менеджеру відділу збуту необхідно прийняти рішення скільки продукції необхідно відправити з кожного заводу у кожен магазин роздрібної торгівлі з точки зору мінімізації витрат, якщо продукція перевозиться вантажівками, а витрати на транспортування одиниці продукції наведено у табл. 3*. Таблиця 3
*Індивідуальні вихідні дані формуються шляхом корегування значень табл. 3 на номер студента за журналом викладача наступним чином: Х+10*N, де Х – значення з табл. 3, N – номер за журналом. Як зміняться витрати за умови коли потужність заводу №9 складатиме 900 одиниць продукції? Яке рішення варто прийняти у випадку коли замовлення магазину №7 склало 800 одиниць продукції (коли попит перевищує пропозицію) та якими при цьому будуть мінімальні витрати? Чи зміниться картина постачань та загальний обсяг витрат, якщо, у силу організаційних умов, стане неможливим постачати продукцію з заводу №6 у магазин №1?
Порядок виконання роботи. 2.1. Створити файл Microsoft Excel. 2.2. Скопіювати вихідні дані та скорегувати їх на власний номер за журналом. 2.3. Сформувати таблицю обсягів перевезень та обмеження для потужності заводів і попиту магазинів. 2.3.1. Формуємо таблицю обсягів перевезень (табл. 4). Таблиця 4
2.3.2. Формалізуємо обмеження для потужності заводів і попиту магазинів (доповнюємо таблицю 4). 2.3.2.1 для збалансованої транспортної моделі
Пояснення: Оскільки сума потужностей 10 заводів у поточному періоді (пропозиція – 5000 одиниць продукції) дорівнює затребуваній кількості товару роздрібними магазинами (попит – 5000 одиниць продукції), модель збалансована. Обмеження моделі повинні вказувати на те, що кожен із наявних заводів повинен виготовити кількість продукції рівну своїй реальній потужності (обмеження =), для того, щоб задовольнити попит, а також, у кожен із магазинів повинно бути відвантажено продукції на рівні замовленого ними обсягу одиниць (обмеження =).
2.4. Сформувати таблицю загальних витрат (табл. 5) Таблиця 5
Для визначення загальних витрат використовуємо наступну формулу:
де
2.5. Використовуючи Надстройку Microsoft Excel «Пошук рішення» знайти мінімальний обсяг загальних витрат, прийнявши цільовою комірку загальних витрат, змінюючи комірки обсягу перевезень і додавши визначені раніше обмеження. 2.6. Визначити мінімальний рівень витрат за умови збільшення потужності заводу № 9. 2.6.1 Сформувати таблицю 4 з обмеженнями для випадку, коли пропозиція перевищує попит:
*Резерв по обсягу пропозиції для кожного з заводів дорівнює різниці між потужністю заводу та його обсягом виробництва попитом (сума значень резерву по усіх заводах повинна дорівнювати загальній сумі не затребуваної пропозиції) Пояснення: Оскільки сума потужностей 10 заводів у поточному періоді (пропозиція – 5200 одиниць продукції) більша затребуваної кількості товару роздрібними магазинами (попит – 5000 одиниць продукції), модель не збалансована. Обмеження моделі повинні вказувати на те, що будь-який із наявних заводів не може виготовити продукції більше своєї реальної потужності (обмеження ≤), а також, у кожен із магазинів повинно бути відвантажено продукції на рівні замовленого ними обсягу одиниць (обмеження =). 2.6.2 Повторити пп.2.4-2.5 2.7. Визначити мінімальний рівень витрат за умови збільшення замовлення магазину № 7. ВАРІАНТ 1 2.7.1 Сформувати таблицю 4 з обмеженнями для випадку коли попит перевищує пропозицію
*Резерв по обсягу попиту дорівнює різниці між обсягом замовлення кожного магазину та реально задоволеним попитом (сума значень резерву по усіх магазинах повинна дорівнювати загальному не задоволеному попиту) Пояснення: Оскільки сума потужностей 10 заводів у поточному періоді (пропозиція – 5000 одиниць продукції) менше затребуваної кількості товару роздрібними магазинами (попит – 5200 одиниць продукції), модель не збалансована. Обмеження моделі повинні вказувати на те, що будь-який із наявних заводів повинен виготовити кількість продукції рівну своїй реальній потужності (обмеження =), а також, у кожен із магазинів повинен бути відвантажений весь наявний обсяг одиниць продукції (обмеження ≤). 2.7.2 Повторити пп.2.4-2.5 ВАРІАНТ 2 2.7.1. Ввести в модель фіктивний відправний пункт (Завод №11ф), потужність якого у точності відповідатиме різниці між загальним попитом та пропозицією.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

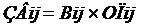 ,
,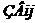 - загальні витрати на транспортування продукції з і-го заводу у j-й магазин роздрібної торгівлі;
- загальні витрати на транспортування продукції з і-го заводу у j-й магазин роздрібної торгівлі;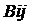 - питомі витрати на транспортування одиниці продукції з і-го заводу у j-й магазин роздрібної торгівлі (табл. 3);
- питомі витрати на транспортування одиниці продукції з і-го заводу у j-й магазин роздрібної торгівлі (табл. 3);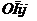 - обсяг перевезень продукції з і-го заводу у j-й магазин (табл. 4).
- обсяг перевезень продукції з і-го заводу у j-й магазин (табл. 4).