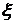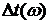Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
И фазо-частотной характеристик системы»ЛАБОРАТОРНАЯ РАБОТА № 3
«Экспериментальное построение амплитудно-частотной и фазо-частотной характеристик системы»
1. ЦЕЛЬ РАБОТЫ Ознакомиться на примере математической модели системы с принципом экспериментального построения графиков АЧХ и ФЧХ системы для дальнейшего их анализа.
2. УКАЗАНИЯ К САМОСТОЯТЕЛЬНОЙ РАБОТЕ При подготовке к лабораторной работе необходимо изучить тему: «Типовые динамические звенья» по литературе [1], [2]. Составить схемы моделей динамических звеньев в соответствии с вариантом задания.
3. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Пусть задано описание передаточной функции системы Сделав преобразование Фурье (Лапласа), можно получить следующее описание Комплекснозначная функция Обозначив модули соответствующих функций можно получить следующее описание где Функции Если передаточная функция представлена полиномиальным выражением в виде (3.1), то АФЧХ системы можно представить следующим образом  где
Функции Из (3.6) с учетом (3.7) и (3.8) можно записать выражения для АЧХ и ФЧХ На рис. 3.1 представлены типовые АЧХ и ФЧХ системы.
Рис. 3.1. АЧХ и ФЧХ системы Частотные характеристики определяются следующими показателями: · показатель колебательности · резонансная частота · полоса пропускания системы — интервал от · частота среза (на рис. 3.1 условно принято Частота среза косвенно характеризует длительность переходного процесса; справедливо соотношение Таким образом, можно сделать важный вывод: чем шире полоса пропускания, тем система является более быстродействующей. Далее рассмотрим закон преобразования гармонических сигналов линейными системами, имеющими
Рис. 3.2. Преобразование гармонических сигналов Имеем (рассматривается установившийся режим работы системы, для чего верхний предел интегрирования берется равным ¥) тогда Результат имеет вид Результат (3.15) можно трактовать так: если на вход системы подается косинусоидальный сигнал с амплитудой Полученный факт используют для экспериментального определения имеющее конкретную угловую частоту В результате в системе возникнет переходный процесс (имеет место составляющая
Логарифмической амплитудно-частотной характеристикой (ЛАЧХ или ЛАХ) системы называется график функции где
Рис. 3.3. Экспериментальное определение частотных характеристик Единицей измерения является децибел. По оси абсцисс откладывается частота w [с–1] в логарифмическом масштабе (рис. 3.4). Равномерной единицей на оси абсцисс является декада. Декада представляет собой промежуток, на котором значение частоты увеличивается в 10 раз (рис. 3.4). Частота Логарифмической фазовой частотной характеристикой (ЛФЧХ или ЛФХ) называется график зависимости При построении логарифмической фазовой частотной характеристики отсчет углов j идет по оси ординат в обычном масштабе в угловых градусах. По оси абсцисс откладывается по-прежнему частота Важно иметь в виду, что ось абсцисс соответствует значению
Рис. 3.4. Логарифмические частотные характеристики
4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 4.1. Ознакомиться с теоретической частью. 4.2. В соответствии с вариантом задания (см. табл. 3.1) промоделировать работу системы – колебательного звена, получив выходной сигнал системы на поданное на вход синусоидальное воздействие. Параметрами входного синусоидального сигнала выбрать начальную фазу, равную нулю и амплитуду, равную единице. Таким образом,
Таблица 3.1 Варианты параметров моделей
function dx=model1(t,x) global w; k = 1; T = 2; xi = 0.2; dx=zeros(2,1); y=sin(w*t); a2 = T^2; a1 = 2 * xi * T; a0 = 1; b0 = k; dx(1)=x(2); dx(2)= 1 / (a2) * (b0 * y - (a1 * x(2) + a0 * x(1)));
clear all; global w T = 3000; w = 0.01; X0=[0,0]; options=odeset('AbsTol',[1e-8,1e-8],'RelTol',1e-8); [t,x]=ode45('model1',[0,T],X0,options); Ax=max(x(round(length(x)/2):length(x),1)); % нормирующий коэффициент
% Определение АЧХ по максимальному установившемуся значению x(t) figure plot(t,x(:,1),'b-','LineWidth',2); hold on; y=sin(w*t); plot(t,y,'g-','LineWidth',2); legend('x(t)','y(t)'); grid on; xlabel('t, c'); ylabel('x_i(t)'); title(strcat('\omega=', num2str(w), ' Гц, A_x=')); annotation('arrow',[0.13 0.13],[0.13 0.95], 'HeadStyle', 'plain'); annotation('arrow',[0.11 0.92],[0.11 0.11], 'HeadStyle', 'plain');
% Выделение максимальных значений на графике для определения фазы x1 = x(:, 1); % DT = 2 * pi / w; steps = ceil(3 * DT / mean(diff(t))); idx_2 = length(t); idx_1 = length(t) - steps + 1; X1 = x1(idx_1 : idx_2); Y = y(idx_1 : idx_2); Xt = t(idx_1 : idx_2); X1_src = X1; Y_src = Y; % X1_MAX_IDX = []; Y_MAX_IDX = []; for k = 1 : 3 [~, X1_max_idx] = max(X1); dt = ceil(0.1 * DT / mean(diff(t))); % отступ 10% tidx_1_x = max(X1_max_idx - dt, 1); tidx_2_x = X1_max_idx + dt; X1(tidx_1_x : tidx_2_x) = 0;
[~, Y_max_idx] = max(Y); tidx_1_y = max(Y_max_idx - dt, 1); tidx_2_y = Y_max_idx + dt; Y(tidx_1_y : tidx_2_y) = 0;
X1_MAX_IDX = [X1_MAX_IDX, X1_max_idx]; Y_MAX_IDX = [Y_MAX_IDX, Y_max_idx]; end
% Определение ФЧХ (разности dt между максимумами y(t) и x(t)) figure plot(Xt, X1_src / Ax, 'b-', 'LineWidth', 2); hold on; plot(Xt, Y_src, 'g-', 'LineWidth', 2); plot(Xt(X1_MAX_IDX), X1_src(X1_MAX_IDX) / Ax, 'bo'); plot(Xt(Y_MAX_IDX), Y_src(Y_MAX_IDX), 'go'); grid on legend('x(t) / A_x', 'y(t)'); title(strcat('\omega=', num2str(w), ' Гц, \phi=')); xlabel('t, c'); ylabel('x_i(t) / A_x'); annotation('arrow',[0.13 0.13],[0.13 0.95], 'HeadStyle', 'plain'); annotation('arrow',[0.11 0.92],[0.11 0.11], 'HeadStyle', 'plain');
4.3. Варьируя частоту синусоидального сигнала, заполнить таблицу 3.2. Для расчета w=[0.01, …, 10]; Aw=[1, …, 0.0006]; dt=[-2.01, …, -0.08]; Tw=2*pi./w; phi=dt./Tw*360 L=20*log10(Aw) Таблица 3.2 Зависимость АЧХ и ФЧХ от частоты
4.4. Построить в MATLAB на основе данных таблицы 3.2 зависимость в виде графика
figure(); plot(w, Aw, 'LineWidth',2); grid on; title('График АЧХ'); ylabel('A(\omega)'); xlabel('\omega, Гц');
figure(); plot(w, phi, 'LineWidth',2); grid on; title('График ФЧХ'); ylabel('\phi(\omega), град.'); xlabel('\omega, Гц');
4.5. Построить график логарифмической амплитудно-частотной характеристики figure(); semilogx(w, L, 'LineWidth',2); grid on title('График логарифмической АЧХ'); ylabel('L(\omega), дБ'); xlabel('\omega, декады Гц');
4.6. Промоделировать колебательное звено в пакете MATLAB при помощи команды tf. Построить графики ЛАЧХ и ЛФЧХ командой bode и сравнить с полученными результатами.
k=…; T=…; xi=…; W=tf([k],[T^2,2*T*xi,1]); figure(); bode(W);
4.7. Промоделировать АФЧХ колебательного звена в пакете MATLAB при помощи команды nyquist. Отключить отрицательные частоты, выбрав в контекстном меню на графике пункт Show/Negative frequencies. Построить на тот же график полученный в результате эксперимента годограф АФЧХ. При этом фазу перевести из градусов в радианы для совмещения с графиком диаграммы Найквиста. Сравнить с полученными результатами. Сделать выводы.
figure(); nyquist(W); hold on; polar(phi*pi/180, Aw, 'r-'); title('Годограф АФЧХ');
Замечание:При программировании в математическом пакете MatLab целая часть отделяется от дробной точкой, а не запятой.
5. СОДЕРЖАНИЕ ОТЧЕТА Отчет должен содержать следующие разделы: 1. Цель работы. 2. Порядок выполнения работы. 3. Исходные данные. 4. Графики переходных процессов, проходящих в системе, в результате отработки входного синусоидального воздействия. 5. Таблица 3.2 с результатами измерений. 6. Графики АЧХ, ФЧХ, ЛФЧХ, полученные в результате экспериментальных измерений. 7. Точные графики ЛАЧХ и ЛФЧХ, построенные для заданного звена. 8. Выводы. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 176. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . (3.1)
. (3.1) (3.2)
(3.2)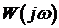 называется комплексной частотной характеристикой системы (КЧХ) или амплитудно-фазовой частотной характеристикой (АФЧХ).
называется комплексной частотной характеристикой системы (КЧХ) или амплитудно-фазовой частотной характеристикой (АФЧХ).

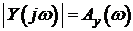 ,
, (3.3)
(3.3) (3.4)
(3.4) (3.5)
(3.5) и
и  определяемые зависимостями (3.4), (3.5), называются соответственно амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристиками.
определяемые зависимостями (3.4), (3.5), называются соответственно амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристиками. (3.6)
(3.6)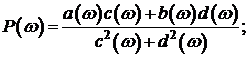 (3.7)
(3.7)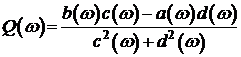 , (3.8)
, (3.8) ,
,  – действительные части соответствующих полиномов числителя и знаменателя;
– действительные части соответствующих полиномов числителя и знаменателя;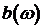 ,
,  – мнимые части полиномов числителя и знаменателя.
– мнимые части полиномов числителя и знаменателя. и
и  называются соответственно действительной и мнимой частотными характеристиками.
называются соответственно действительной и мнимой частотными характеристиками. (3.9)
(3.9) (3.10)
(3.10)
 — характеризует склонность системы к колебаниям: чем выше
— характеризует склонность системы к колебаниям: чем выше  тем менее качественна система (как правило, в реальных системах
тем менее качественна система (как правило, в реальных системах 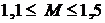 );
); — частота, при которой АЧХ имеет максимум (на этой частоте гармонические колебания имеют наибольшее усиление);
— частота, при которой АЧХ имеет максимум (на этой частоте гармонические колебания имеют наибольшее усиление);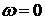 до
до  при котором выполняется условие
при котором выполняется условие (3.11)
(3.11)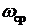 — частота, при которой АЧХ системы принимает значение, равное
— частота, при которой АЧХ системы принимает значение, равное  т.е.
т.е. (3.12)
(3.12) ).
). (3.13)
(3.13) — ФЧХ (рис. 3.2).
— ФЧХ (рис. 3.2).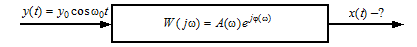


 (3.14)
(3.14) (3.15)
(3.15) то на выходе в установившемся режиме имеет место также косинусоидальный сигнал с той же частотой, но уже с другими амплитудой и фазой: амплитуда выхода равна
то на выходе в установившемся режиме имеет место также косинусоидальный сигнал с той же частотой, но уже с другими амплитудой и фазой: амплитуда выхода равна 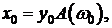 а сигнал имеет сдвиг фазы
а сигнал имеет сдвиг фазы 
 Для определения одной точки
Для определения одной точки  и
и  на вход системы надо подать гармоническое воздействие
на вход системы надо подать гармоническое воздействие (3.16)
(3.16)
 ) и установившиеся колебания с частотой
) и установившиеся колебания с частотой 
 , на выходе будут иметь место установившиеся колебания с частотой
, на выходе будут иметь место установившиеся колебания с частотой 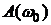 и
и  ) определяется зависимостями
) определяется зависимостями (3.17)
(3.17) вида
вида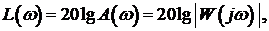 (3.18)
(3.18) (3.19)
(3.19) (3.20)
(3.20)
 на которой
на которой  то начало координат чаще всего берется в точке
то начало координат чаще всего берется в точке  (исключая точку
(исключая точку  так как
так как  ). Таким образом, начало координат можно брать в любой точке (в зависимости от интересующего нас диапазона частот, например:
). Таким образом, начало координат можно брать в любой точке (в зависимости от интересующего нас диапазона частот, например: 


 или другие), исключая точку
или другие), исключая точку 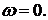 Обычно начало координат помещают в точке
Обычно начало координат помещают в точке 

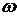 в логарифмическом масштабе.
в логарифмическом масштабе. т.е. прохождению амплитуды входного сигнала через звено в натуральную величину. Верхняя полуплоскость ЛАЧХ соответствует значениям
т.е. прохождению амплитуды входного сигнала через звено в натуральную величину. Верхняя полуплоскость ЛАЧХ соответствует значениям  (усиление амплитуды), а нижняя полуплоскость — значениям
(усиление амплитуды), а нижняя полуплоскость — значениям  (ослабление амплитуды).
(ослабление амплитуды).
 . Начальные условия нулевые. На монитор выводить графики сигналов
. Начальные условия нулевые. На монитор выводить графики сигналов  и
и  . Продолжительности интервалов наблюдения выбрать самостоятельно, чтобы в окно попадал интервал сигнала, превышающий время установления колебаний, но не менее 300 с. Для построения графиков функций можно воспользоваться скриптами из лабораторной работы № 1, модифицировав систему дифференциальных уравнений в соответствии с заданием.
. Продолжительности интервалов наблюдения выбрать самостоятельно, чтобы в окно попадал интервал сигнала, превышающий время установления колебаний, но не менее 300 с. Для построения графиков функций можно воспользоваться скриптами из лабораторной работы № 1, модифицировав систему дифференциальных уравнений в соответствии с заданием.