
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Из произведения элементов главной диагонали вычесть произведение элементов побочной.К а ф е д р а«Высшая математика и Прикладная информатика»
ЛИНЕЙНАЯ АЛГЕБРА, АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ, НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА (для заочного факультета)
Учебно-методическое пособие по специальным разделам высшей математики
Самара 2008
УДК 517.531, 519.2
Линейная алгебра, аналитическая геометрия, начала математического анализа (для заочного факультета): Учеб.-метод. пособ. по специальным разделам высшей математики/ Л.В. Лиманова, Л.А. Муратова; Самар. гос. техн. ун-т. Самара, 2008. 27 с.
Представлены задачи и их решения из следующих разделов курса высшей математики: «Линейная алгебра», «Аналитическая геометрия», «Математический анализ». Для студентов заочного факультета СамГТУ.
Ил.2. Библиогр.: 6 назв.
Печатается по решению редакционно-издательского совета СамГТУ
В соответствии с рабочими программами курса математики в 1-2 семестрах на заочном отделении НФ СамГТУ данная работа включает такие разделы, как линейная алгебра, аналитическая геометрия, теория пределов, дифференциальное исчисление. Работа состоит из набора типовых задач из указанных разделов с подробными решениями и необходимым теоретическим материалом. Кроме того в приложении 1 представлен тренировочный тест с ответами для самоконтроля знаний. Материал данной работы рекомендуется использовать для подготовки к контрольной работе и экзамену по математике за 1 курс. ЗАДАЧИ И РЕШЕНИЯ
РАЗДЕЛ I ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Определители и системы линейных уравнений  1.1 Определители 2го порядка
Пусть дана система 2х линейных уравнений с 2я неизвестными.
Решаем эту систему методом исключения неизвестных. Исключим у. Для этого 1е уравнение умножаем на а22, второе на –а12, затем уравнения складываем. После преобразований получаем
Если
Число
Выражение, стоящее в числителе, тоже является определителем 2го порядка
Данные выражения являются символической записью определителя второго порядка. По определению определитель–это число, поэтому для вычислений символическая запись требует раскрытия или вычисления. Для облегчения процесса вычисления применяют различные схемы. Сначала об элементах определителя: Правило вычисления определителя 2го порядка Из произведения элементов главной диагонали вычесть произведение элементов побочной.
Примеры: 1) 2) Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается Определители получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
Формулы Крамера для нахождения неизвестных:
Найти значения
Этот вывод следует из следующей теоремы. Теорема Крамера :Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка. 1.2 Определители 3го порядка. Определитель 3го порядка есть число, вычисляемое следующим образом:
Кроме уже известных вам элементов определителя введем новые. Минор Выделим в определителе 3го порядка элемент Например
Алгебраическое дополнение элемента
Схема знаков Например
Для упрощения вычисления определителя имеется несколько правил (схем). Правило (формула) Лапласа) Сумма произведений элементов
Для определителя 3го порядка:
Пример 3:
Можно видеть, что формула Лапласа позволяет понижает порядок определителя, руководствуясь ею можно вычислить определитель любого порядка.
1.3 Свойства определителей Мы изучим свойства общие для определителей любого порядка. Но будем рассматривать их на примере определителя 3го порядка. 1) Величина определителя не изменится, если его строки и столбцы поменять местами. Такая операция называется транспонированием определителя и обозначается
2) При перестановке 2х строк (или столбцов) определитель меняет знак.
Проверка вычислением. 3) Определитель с двумя одинаковыми строками (столбцами) равен нулю. 4) Общий множитель элементов строки (столбца) можно вынести за знак определителя. 5) Если все элементы некоторой строки (столбца) равны нулю, то определитель равен нулю. 6) Если соответствующие элементы 2х строк (столбцов) пропорциональны, то такой определитель равен нулю.
7) Сумма произведений элементов
7) Пусть определитель имеет следующий вид:
Доказать можно разложением по элементам первого столбца. 8) Если к элементам некоторой строки (столбца) прибавить элементы другой строки (столбца) предварительно умноженные на одно и тоже число, то величина определителя не изменится. Это свойство позволяет производить упрощение определителя путем образования в строке или столбце нулей. Раскладывая затем определитель по строке (столбцу), содержащему нули можно получить и определитель более низкого порядка. Пример 4: Вычислить определитель
1.4 Решение систем линейных уравнений с помощью определителей Будем рассматривать квадратнуюсистему (1.6), в ней количество неизвестных и количество уравнений одинаково. Применим метод исключения неизвестных. Для исключения неизвестных .
Эти формулы дают единственное решение системы. 2) Пусть Система не совместна, т.к. (1.7) не выполняются. 3) Пример1) Решить систему Решение Вычислим определитель системы:
Так как Δ =-8 ≠ 0, то система имеет единственное решение, которое можно найти по формулам Крамера:
Для этого вычислим определители Δ1,Δ2иΔ3:
Следовательно, Ответ:
Пример 2). Решить систему
Решение. 1) Определитель системы
2) Определители для неизвестных:
Система несовместна. Ответ Пример3).Решить систему
Задача 1. Вычислить определитель Решение. Определитель второго порядка
Поэтому Задача 2. Вычислить определитель Решение. Определитель третьего порядка можно вычислить по формуле
При этом полезна следующая схема. Первые три слагаемых – это произведения элементов, попавших на главную диагональ и в вершины двух треугольников (рис.1). Три слагаемых в скобках – это произведения элементов, попавших на побочную диагональ и в вершины двух других треугольников (рис.2).
|
||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 135. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1.1)
(1.1) .
. , то можно найти х
, то можно найти х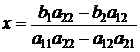 . (1.2)
. (1.2) называется определителем 2го порядка и обозначается
называется определителем 2го порядка и обозначается .
.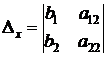 .
.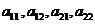 . Индексы указывают номер строки и номер столбца на пересечении которых находится элемент. Элементы с одинаковыми первыми индексами образуют строки, с одинаковыми вторыми–столбцы, элементы с одинаковыми первым и вторым индексами образуют главную диагональ, c индексами 1,2 и 2,1 – побочную диагональ.
. Индексы указывают номер строки и номер столбца на пересечении которых находится элемент. Элементы с одинаковыми первыми индексами образуют строки, с одинаковыми вторыми–столбцы, элементы с одинаковыми первым и вторым индексами образуют главную диагональ, c индексами 1,2 и 2,1 – побочную диагональ.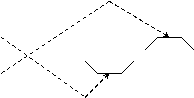
 .
. ;
;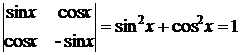 ;
; (дельта).
(дельта).
 ;
; .
. .
. и
и  возможно только при условии, если
возможно только при условии, если .
. .
. и вычеркнем i-ую строку и k-ый столбец. Оставшиеся элементы образуют определитель второго порядка, который и называют минором Mik элемента
и вычеркнем i-ую строку и k-ый столбец. Оставшиеся элементы образуют определитель второго порядка, который и называют минором Mik элемента  .
. .
. для алгебраических дополнений определителя 3го порядка.
для алгебраических дополнений определителя 3го порядка. .
. – такая запись называется разложением определителя по столбцу k.
– такая запись называется разложением определителя по столбцу k. – это разложение по строке i.
– это разложение по строке i.
 .
.












 , таким образом
, таким образом .
.

 .
. .
. , его можно записать в виде суммы 2х определителей
, его можно записать в виде суммы 2х определителей .
.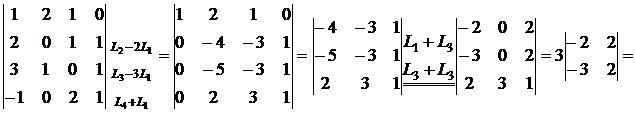
 .
. умножаем уравнения системы на алгебраические дополнения первого столбца определителя системы составленного из коэффициентов при неизвестных
умножаем уравнения системы на алгебраические дополнения первого столбца определителя системы составленного из коэффициентов при неизвестных 1) Из этой системы при
1) Из этой системы при  получаем формулы Крамера, позволяющие определить неизвестные системы
получаем формулы Крамера, позволяющие определить неизвестные системы ;
;  ;
; 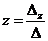 . (1.3)
. (1.3) , но один из определителей для неизвестных отличен от нуля
, но один из определителей для неизвестных отличен от нуля 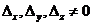 .
. . В этом случае система или не имеет решений, или имеет их бесчисленное множество. (Или несовместна, или неопределенна).
. В этом случае система или не имеет решений, или имеет их бесчисленное множество. (Или несовместна, или неопределенна).
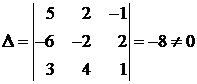 .
.
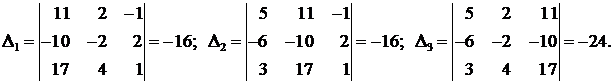



 .
. .
. .
.
 .
. равен разности между произведениями элементов главной диагонали (a1 и b2) и побочной (b1 и a2), то есть
равен разности между произведениями элементов главной диагонали (a1 и b2) и побочной (b1 и a2), то есть .
. .
. .
. .
.