
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Западная Европа Средневековье, IV—XV векаАрабские страны В VII в. в Аравии возникла новая религия – ислам, основанная Мухаммедом. Приверженцы этой религии называются мусульманами. Преемники Мухаммеда – халифы принялись покорять неверных и за VII в. завоевали Вавилон, Персию, Египет и весь север Африки. Население этих стран со временем стало считать себя арабами и приверженцами ислама. В VIII – IX вв. арабы проникли на европейский континент и завоевали Испанию и юг Италии, а на востоке – Среднюю Азию, часть Закавказья и Индии. Образовался огромный халифат от Испании на западе до Индии на востоке. Столицей халифата была сначала Дамаск, а затем – новый город Багдад. Одновременно на территории халифата формируется феодальный строй. Жители халифата занимались земледелием и, следовательно, орошением полей, в Багдаде и других городах ведется большое строительство, развиваются ремесла и торговля. В завоеванных странах халифы обнаружили более высокую культуру и науку, чем в халифате, а поэтому стали вывозить в Багдад ученых, строителей и ремесленников. Арабский язык стал международным языком науки. К Х в. арабский халифат распадается: завоеванные страны, сохраняя религиозное подчинение Багдаду, во всех других отношениях становятся независимыми. В XI в. арабы были выбиты из Италии, а вот изгнание их из Испании растянулось с Х по XY в. Сначала наука была сосредоточена в Багдаде, но по мере появления новых арабских государств возникают и новые научные центры. Во многих столицах появляются обсерватории. Широкую известность, в том числе и за пределами арабских стран получили врач Авиценна, или Ибн Сина (Х в.), поэт и одновременно ученый Омар Хайям (XI – XII вв.), директор Самаркандской обсерватории Улугбек (XV в.). Улугбек был внуком знаменитого среднеазиатского завоевателя Тимура и стал султаном в Самарканде. Но это был странный для того времени султан: он больше был занят наукой и был казнен по тайному приговору церковного суда, члены которого сочли его еретиком.  Математикой, в основном, занимались выходцы из Средней Азии, Персии и Вавилона. Ученые арабских государств были хорошо знакомы с математикой как Запада, так и Востока, в частности, с индийской математикой. Основные сочинения классиков математики древней Греции: Евклида, Архимеда, Аполлония, Диофанта и др. были переведены на арабский язык. Весьма значительная часть этих сочинений именно поэтому дошла до Западной Европы, когда их стали позднее переводить с арабского на латинский язык. Арифметика. В Странах ислама применялись два типа нумерации: алфавитная, а следовательно, десятичная непозиционная, и десятичная позиционная, заимствованная у индийцев. В последней применялись цифры, похожие на индийские, с некоторыми отличиями между восточно-арабскими и западно-арабскими цифрами. Действия над натуральными числами производились на счетной доске, посыпанной песком или пылью, - как в Индии. Из дробей арабские математики знали только обыкновенные дроби, но в астрономии ученые пользовались вавилонскими шестидесятеричными дробями. Дроби большей частью записывали по-индийски: числитель над знаменателем, а целую часть смешанного числа – над числителем. Арифметические задачи решались следующих типов: задачи, возникавшие в торговом деле, при распределении налогов, разделе наследства и др.. При решении использовались пропорциональное деление и тройное правило. Арабы широко пользовались также иррациональными числами. Алгебра. В алгебре арабские ученые были, в общем, самостоятельны и оригинальны. Одним из крупнейших арабских математиков был Мухаммед ибн-Муса ал-Хорезми (VIII-IX вв.). Он был узбеком, выходцем из Хорезма, города в Средней Азии, жил и работал в Багдаде. Известен как автор трактата по арифметике, предположительно называвшегося «Книга о сложении и вычитании по исчислению индийцев». По этому сочинению арабы впервые знакомились с индийской десятичной позиционной нумерацией. При переводе его на латинский язык от имени автора образовалось слово «алгоритм», которое первоначально обозначало всю систему десятичной позиционной арифметики. Но главное сочинение ал-Хорезми посвящено алгебре. Оно носит заглавие «Краткая книга об исчислении ал-джабра и ал-мукабалы». Под «ал-джабром» автор понимает перенос отрицательных членов из одной части уравнения в другую со знаком плюс, а под «ал-мукабалой» - приведение подобных членов в обеих частях уравнения. От слова 2 ал-джабр» произошел современный термин «алгебра». Алгебраической символики у ал-Хорезми, как и вообще в арабской математике, нет, уравнения читаются словесно. Не были известны и отрицательные уравнения. Он делит эти уравнения на следующие типы: 1) 2) 3) 4) 5) где a,b,c – данные положительные рациональные числа. Для уравнения каждого типа формируется простой алгоритм решения. Обоснование правила дается только x для уравнений четвертого и шестого типов, на примерах, но общим образом. Например, правило решения уравнения
Фактически это прием выделения полного квадрата в левой части уравнения, только в геометрической форме. После ал-Хорезми ученые Абу Камил (IX-X вв.) и ал-Кархи (X-XI вв.) изложили решение квадратных уравнений более подробно, в методический обработанном виде, рассмотрели правила тождественных преобразований алгебраических выражений. В частности, у ал-Кархи мы находим суммирование арифметической и геометрической прогрессий, формулы сумм
а также решение трехчленных уравнений. Ученые арабских стран занялись решением уравнений третьей и четвертой степени. С помощью кубических уравнений они решали задачу о трисекции угла, пришедшую из древней Греции. Постепенно возникла проблема построения общей теории кубических уравнений. С этой проблемой справился Омар Хайям, имя которого упоминалось раньше. Прежде всего Омар Хайям – знаменитый персидский поэт. Что касается кубических уравнений, то им написан «Трактат о доказательствах задач алджабра». Слово «ал-джабр» он употребляет для названия алгебры и трактует алгебру как самостоятельную науку – науку о решении уравнений. Для решения кубических уравнений он использует геометрию – конические сечения, а име6нно параболу, равностороннюю гиперболу и окружность. В зависимости от решения Хайям делит кубические уравнения на 14 типов. Впрочем, впоследствии оказалось, что его классификация неполна. Важную роль в арабской математике сыграл ал-Каши (XIV-XVв). Главное его сочинение – «Ключ арифметики». Это мастерски написанное руководство по элементарной математике, непревзойденное во всей средневековой литературе по богатству содержания, ясности и четкости изложения. В этом сочинении, в частности, вводятся, независимо от китайской математики, десятичные дроби. Открытие десятичных дробей не было замечено и в должной мере оценено ни другими арабскими учеными, ни учеными Западной Европы, поэтому европейским математикам позднее пришлось открывать их заново. Сам ал-Каши в другой работе находил число π и записал его десятичной дробью с 17 десятичными знаками. Из алгебраических сведений в сочинении «Ключ арифметики» отметим извлечение корней любой степени методом Горнера, формулу бинома Ньютона, таблицу биномиальных коэффициентов, треугольник Паскаля, связанный с этим, таблицей, и тождество С Геометрия. В геометрии результаты арабских ученых сравнительно скромны. Они знали верные формулы площадей и объемов (мы находим эти формулы уже в работе ал-Хорезми «Краткая книга об исчислении ал-джабра и ал-мукабалы»). Несколько ученых занимались комментированием «Начал» Евклида, при этом особым вниманием пользовалась теория параллельных. Были попытки доказательства пятого постулата. Отдельные ученые занимались вычислением площадей и объемов методами Архимеда, получив здесь некоторые новые результаты в сравнении с Архимедом. Тригонометрия. Арабские ученые заимствовали элементы тригонометрии у индийцев. Они развивали как прямолинейную, так и сферическую тригонометрию, особенно сферическую, так как именно она в первую очередь важна для астрономии. Некоторые ученые занимались решением прямоугольных треугольников с помощью тригонометрии. Ведущая фигура здесь –Насир ад-Дин ат-Туси( XIIIв.)Его сочинение «Трактат о полном четырехстороннике» посвящено тригонометрии. В нем впервые тригонометрия рассматривается как самостоятельная наука – наука о решении треугольников; до тех пор сведения по тригонометрии включались в качестве вспомогательного материала в книге по астрономии. Это первое полное изложение всей системы тригонометрии, доведенное до основных случаев решения косоугольных треугольников на плоскости и на сфере. Часть результатов получена самим ат-Туси. Ученые, занимавшиеся астрономией и тригонометрией, составляли таблицы значений тригонометрических величин, прежде всего синуса. Со временем эти таблицы совершенствовались и уточнялись.
Западная Европа Средневековье, IV—XV века В V веке наступил конец Западной Римской империи, и территория Западной Европы надолго превратилась в поле непрестанных сражений с завоевателями и разбойниками (гунны, готы, венгры, арабы, норманны и т. п.). Развитие науки прекратилось. Потребность в математике ограничивается арифметикой и расчётом календаря церковных праздников, причём арифметика изучается по древнему учебнику НикомахаГеразского в сокращённом переводе Боэция на латинский. Среди немногих высокообразованных людей можно отметить ирландца Беду Достопочтенного (он занимался календарём, пасхалиями, хронологией, теорией счёта на пальцах) и монаха Герберта, с 999 года — римского папы под именем Сильвестр II, покровителя наук; ему приписывают авторство нескольких трудов по астрономии и математике. Популярный сборник занимательных математических задач издал англосаксонский поэт и учёный Алкуин (VIII век). Стабилизация и восстановление европейской культуры начинаются с XI века. Появляются первые университеты (Салерно, Болонья). Расширяется преподавание математики: в традиционный квадривиум входили арифметика, геометрия, астрономия и музыка. Первое знакомство европейских учёных с античными открытиями происходило в Испании. В XII веке там переводятся (с греческого и арабского на латинский) основные труды великих греков и их исламских учеников. С XIV века главным местом научного обмена становится Византия. Особенно охотно переводились и издавались «Начала» Евклида; постепенно они обрастали комментариями местных геометров. Единственным относительно крупным математиком за всю после-античную историю Византии был Максим Плануд, комментатор Диофанта и популяризатор десятичной системы. В конце XII века на базе нескольких монастырских школ был создан Парижский университет, где обучались тысячи студентов со всех концов Европы, почти одновременно возникают Оксфорд и Кембридж в Британии. Интерес к науке растёт, и одно из проявлений этого — смена числовой системы. Долгое время в Европе применялись римские цифры. В XII—XIII веках публикуются первые в Европе изложения десятичной позиционной системы записи (сначала переводы ал-Хорезми, потом собственные руководства), и начинается её применение. С XIV века индо- арабские цифры начинают вытеснять римские даже на могильных плитах. Только в астрономии ещё долго применялась шестидесятеричная вавилонская арифметика. Первым крупным математиком средневековой Европы стал в XIII веке Леонардо Пизанский, известный под прозвищем Фибоначчи. Основной его труд: «Книга абака» (1202 год, второе переработанное издание — 1228 год). Абаком Леонардо называл арифметические вычисления. Фибоначчи был хорошо знаком (по арабским переводам) с достижениями древних и систематизировал значительную их часть в своей книге. Его изложение по полноте и глубине сразу стало выше всех античных и исламских прототипов, и долгое время было непревзойдённым. Эта книга оказала огромное влияние на распространение математических знаний, популярность индийских цифр и десятичной системы в Европе. В книгах «Арифметика» и «О данных числах» Иордана Неморария усматриваются зачатки символической алгебры, до поры до времени не отделившейся от геометрии. В это же время Роберт Гроссетест и Роджер Бэкон призывают к созданию экспериментальной науки, которая на математическом языке сможет описать природные явления. В XIV веке университеты появляются почти во всех крупных странах (Прага, Краков, Вена, Гедельберг, Лейпциг, Базель и др.). Философы из Оксфордского Мертон-Колледжа, жившие в XIV веке и входившие в группу так называемых оксфордских калькуляторов, развивали логико-математическое учение об усилении и ослаблении качеств. Другой вариант этого же учения развивал в Сорбонне Николай Орем. Он ввёл изображение зависимости с помощью графика, исследовал сходимость рядов. В алгебраических трудах он рассматривал дробные показатели степени. Видный немецкий математик и астроном XV века Иоганн Мюллер стал широко известен под именем Региомонтан — латинизированным названием его родного города Кёнигсберг. Он напечатал первый в Европе труд, специально посвящённый тригонометрии. По сравнению с арабскими источниками нового немного, но надо особо отметить систематичность и полноту изложения. Лука Пачоли, крупнейший алгебраист XV века, друг Леонардо да Винчи, дал ясный (хотя не слишком удобный) набросок алгебраической символики. XVI век XVI век стал переломным для европейской математики. Полностью усвоив достижения предшественников, она несколькими мощными рывками вырвалась далеко вперёд. Первым крупным достижением стало открытие общего метода решения уравнений третьей и четвёртой степени. Итальянские математики дельФерро, Тарталья и Феррари решили проблему, с которой несколько веков не могли справиться лучшие математики мира. При этом обнаружилось, что в решении иногда появлялись «невозможные» корни из отрицательных чисел. После анализа ситуации европейские математики назвали эти корни «мнимыми числами» и выработали правила обращения с ними, приводящие к правильному результату. Так в математику впервые вошли комплексные числа. Важнейший шаг к новой математике сделал француз Франсуа Виет. Он окончательно сформулировал символический метаязык арифметики — буквенную алгебру. С её появлением открылась возможность проведения исследований невиданной ранее глубины и общности. В своей книге «Введение в аналитическое искусство» Виет показал примеры мощи нового метода, найдя знаменитые формулы Виета. Символика Виета ещё не была похожа на принятую ныне, современный её вариант позднее предложил Декарт. Третье великое открытие XVI века — изобретение логарифмов (Джон Непер). Сложные расчёты упростились во много раз, а математика получила новую неклассическую функцию с широкой областью применения. В 1585 году фламандец Симон Стевин издаёт книгу «Десятая» о правилах действий с десятичными дробями, после чего десятичная система одерживает окончательную победу и в области дробных чисел. Стевин также провозгласил полное равноправие рациональных и иррациональных чисел, а также (с некоторыми оговорками) и отрицательных чисел. Одновременно растёт престиж математики, в изобилии появляется множество практических задач, требующих решения — в артиллерии, мореплавании, строительстве, промышленности, гидравлике, астрономии, картографии, оптике и др.. И, в отличие от античности, учёные Возрождения не чурались таких задач. Чистых математиков-теоретиков фактически не было. Появляются первые Академии наук. В XVI—XVII веках роль университетской науки падает, появляется множество учёных-непрофессионалов: Стевин — военный инженер, Виет и Ферма — юристы, Дезарг и Рен — архитекторы, Лейбниц — чиновник, Непер, Декарт, Паскаль — частные лица. XVII век В XVII веке быстрое развитие математики продолжается, и к концу века облик науки коренным образом меняется. Рене Декарт исправляет стратегическую ошибку античных математиков и восстанавливает алгебраическое понимание числа (вместо геометрического). Более того, он указывает способ перевода геометрических предложений на алгебраический язык (с помощью системы координат), после чего исследование становится намного эффективнее. Так родилась аналитическая геометрия. Декарт рассмотрел множество примеров, иллюстрирующих огромную мощь нового метода, и получил немало результатов, неизвестных древним. Особо следует отметить разработанную им математическую символику, близкую к современной. Аналитический метод Декарта немедленно взяли на вооружение Валлис, Ферма и многие другие видные математики. Пьер Ферма, Гюйгенс и Якоб Бернулли открывают новый раздел математики, которому суждено большое будущее — теорию вероятностей. Якоб Бернулли формулирует первую версию закона больших чисел. И, наконец, появляется не очень чёткая, но глубокая идея — анализ произвольных гладких кривых с помощью разложения их на бесконечно малые отрезки прямых. Первой реализацией этой идеи был во многом несовершенный метод неделимых (Кеплер, Кавальери, Ферма), и уже с его помощью было сделано множество новых открытий. В конце XVII века идея неделимых была существенно расширена Ньютоном и Лейбницем, и появился исключительно могучий инструмент исследования — математический анализ. Это математическое направление стало основным в следующем, XVIII веке. Теория отрицательных чисел всё ещё находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Комплексные числа считались фиктивными, правила действий с ними были окончательно не отработаны. Более того, было неясно, все ли «мнимые числа» можно записать в виде a+bi или, скажем, при извлечении некоторого корня могут появиться мнимости, не сводящиеся к этой форме (так полагал даже Лейбниц). Только в XVIII веке Даламбер и Эйлер установили, что комплексные числа замкнуты относительно всех операций, включая извлечение корня любой степени. Во второй половине XVII века появляется научная периодика, ещё не специализированная по видам наук. Начало положили Лондон и Париж, но особо важную роль сыграл журнал ActaEruditorum (1682, Лейпциг, на латинском языке). Французская Академия наук издаёт свои записки (Memoires) с 1699 года. Выходили эти журналы редко, и переписка продолжала оставаться незаменимым средством распространения информации. XVIII век XVIII век в математике можно кратко охарактеризовать как век анализа, который стал главным объектом приложения усилий математиков. Способствуя бурному развитию естественных наук, анализ, в свою очередь, прогрессировал сам, получая от них всё более и более сложные задачи. На стыке этого обмена идеями родилась математическая физика. Критика метода бесконечно малых за плохую обоснованность быстро смолкла под давлением триумфальных успехов нового подхода. В науке, благодаря Ньютону, царила механика — все прочие взаимодействия считались вторичными, следствиями механических процессов. Развитие анализа и механики происходили в тесном переплетении; первым это объединение осуществил Эйлер, который убрал из ньютоновской механики архаичные конструкции и подвёл под динамику аналитический фундамент (1736). С этого момента механика стала прикладным разделом анализа. Процесс завершил Лагранж, чья «Аналитическая механика» демонстративно не содержит ни одного чертежа. Одновременно анализ алгебраизировался и окончательно (начиная с Эйлера) отделился от геометрии и механики. Главным методом познания природы становится составление и решение дифференциальных уравнений. После динамики точки настал черёд динамики твёрдого тела, затем — жидкости и газа. Прогрессу в этой области немало способствовал спор о струне, в котором участвовали ведущие математики Европы. Теория тяготения Ньютона поначалу встречала трудности в описании движения Луны, однако работы Клеро, Эйлера и Лапласа ясно показали, что никаких дополнительных сил, кроме ньютоновских, в небесной механике нет. Анализ распространяется на комплексную область. Аналитическое продолжение большинства функций проблем не вызвало, и были обнаружены неожиданные связи между стандартными функциями (формула Эйлера). Затруднения встретились для комплексного логарифма, но Эйлер их успешно преодолел. Были введены конформные отображения, высказана гипотеза о единственности аналитического продолжения. Комплексные функции нашли даже применение в прикладных науках — гидродинамике, теории колебаний (Даламбер, Эйлер). Далеко продвинулись теория и техника интегрирования. Входят в широкое употребление кратные интегралы (Эйлер, Лагранж), причём не только в декартовых координатах. Появляются и поверхностные интегралы (Лагранж, Гаусс). Усиленно разрабатывается теория дифференциальных уравнений, как обыкновенных, так и в частных производных. Математики проявляют исключительную изобретательность при решении дифференциальных уравнений в частных производных, для каждой задачи изобретая свои методы решения. Сформировалось понятие краевой задачи, возникли первые методы её решения. В конце XVIII века было положено начало общей теории потенциала (Лагранж, Лаплас, Лежандр). Для тяготения потенциал ввёл Лагранж (1773, термин предложил Грин в 1828 году). Вскоре Лаплас обнаружил связь потенциала с уравнением Лапласа и ввёл важный класс ортогональных сферических функций. Возникают многообещающее вариационное исчисление и вариационные принципы физики (Эйлер, Лагранж). Лидером математиков XVIII века был Эйлер, чей исключительный талант наложил отпечаток на все основные математические достижения столетия. Именно он сделал из анализа совершенный инструмент исследования. Эйлер существенно обогатил ассортимент функций, разработал технику интегрирования, далеко продвинул практически все области математики. Наряду с Мопертюи он сформулировал принцип наименьшего действия как высший и универсальный закон природы. В теории чисел окончательно легализуются мнимые числа, хотя полная теория их ещё не создана. Доказана (ещё не вполне строго) основная теорема алгебры. Эйлер разработал теорию делимости целых чисел и теорию сравнений (вычетов), завершённую Гауссом. Эйлер ввёл понятие первообразного корня, доказал его существование для любого простого числа и нашёл количество первообразных корней, открыл квадратичный закон взаимности. Он и Лагранж опубликовали общую теорию цепных дробей, и с их помощью решили немало задач диофантова анализа. Эйлер также обнаружил, что в ряде задач теории чисел можно применить аналитические методы. Стремительно развивается линейная алгебра. Первое подробное описание общего решения линейных систем дал в 1750 году Габриэль Крамер. Близкую к современной символику и глубокий анализ определителей дал Александр ТеофилВандермонд (1735—1796). Лаплас в 1772 году дал разложение определителя по минорам. Теория определителей быстро нашла множество приложений в астрономии и механике (вековое уравнение), при решении алгебраических систем, исследовании форм и т. д. В алгебре назревают новые идеи, завершившиеся уже в XIX веке теорией Галуа и абстрактными структурами. Лагранж при исследовании уравнений пятой степени и выше вплотную подходит к теории Галуа (1770), выяснив, что «истинная метафизика уравнений — теория подстановок». В геометрии появляются новые разделы: дифференциальная геометрия кривых и поверхностей, начертательная геометрия (Монж), проективная геометрия (Лазар Карно). Теория вероятностей перестаёт быть экзотикой и доказывает свою полезность в самых неожиданных областях человеческой деятельности. Де Муавр и Даниил Бернулли открывают нормальное распределение. Возникают вероятностная теория ошибок и научная статистика. Классический этап развития теории вероятностей завершили работы Лапласа. Однако приложения её к физике тогда ещё почти отсутствовали (не считая теории ошибок). Центрами математических исследований становятся Академии наук, по большей части государственные. Значение университетов невелико (исключая страны, где академий ещё нет), физико-математические факультеты всё ещё отсутствуют. Ведущую роль играет Парижская академия. Английская школа после Ньютона обособляется и на целый век снижает научный уровень; число видных математиков в Англии XVIII века невелико — де Муавр (французский эмигрант-гугенот), Котс, Тейлор, Маклорен, Стирлинг. Математики становятся профессионалами, любители почти исчезают со сцены. В конце XVIII века появляются специализированные математические журналы, увеличивается интерес к истории науки. Издается двухтомная «История математики» Монтюкла (посмертно переизданная и дополненная до 4 томов). Расширяется издание научно-популярной литературы. XIX век Неоспоримая эффективность применения математики в естествознании подталкивала учёных к мысли, что математика, так сказать, встроена в мироздание, является его идеальной основой. Другими словами, познание в математике есть часть познания реального мира. Многие учёные XVII—XVIII веков в этом и не сомневались. Но в XIX веке эволюционное развитие математики было нарушено, и этот, казавшийся непоколебимым, тезис был поставлен под сомнение. В геометрии, алгебре, анализе появляются многочисленные нестандартные структуры с необычными свойствами: неевклидовы и многомерные геометрии, кватернионы, конечные поля, некоммутативные группы и т. п. Объектами математического исследования всё больше становятся нечисловые объекты: события, предикаты, множества, абстрактные структуры, векторы, тензоры, матрицы, функции, многолинейные формы и т. д. Возникает и получает широкое развитие математическая логика, в связи с чем появилось искушение связать именно с ней коренные основания математики. Георг Кантор вводит в математику предельно абстрактную теорию множеств, а заодно понятие актуальной бесконечности произвольного масштаба. В конце века при попытке обосновать фундамент математики на основе теории множеств были обнаружены противоречия, которые заставили задуматься над непростыми вопросами: что означает «существование» и «истинность» в математике? В целом в XIX веке роль и престиж математики в науке и экономике заметно растут. Соответственно растёт и её государственная поддержка. Математика вновь становится по преимуществу университетской наукой. Появляются первые математические общества: Лондонское, Американское, Французское, Московское, а также общества в Палермо и Эдинбурге. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 200. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (читается: квадраты равны корням);
(читается: квадраты равны корням); =c (квадраты равны числу);
=c (квадраты равны числу);
 (квадрат и корни равны числу);
(квадрат и корни равны числу);
 доказывается с помощью следующего чертежа (рис. 31).
доказывается с помощью следующего чертежа (рис. 31). Площадь заштрихованной фигуры равна
Площадь заштрихованной фигуры равна  т.е. 39. Тогда площадь всего большого квадрата равна, с одной стороны,
т.е. 39. Тогда площадь всего большого квадрата равна, с одной стороны,  , а с другой - 39 + 25 =64. Получаем:
, а с другой - 39 + 25 =64. Получаем:

 С
С 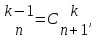 на котором основан треугольник, а также различные методы решения уравнений третьей и четвертой степени, главным образом, геометрические.
на котором основан треугольник, а также различные методы решения уравнений третьей и четвертой степени, главным образом, геометрические.