
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЗУБЧАТЫЕ И ЧЕРВЯЧНЫЕ ПЕРЕДАЧИСтр 1 из 2Следующая ⇒ Раздел №1: Прямозубые зубчатые передачи. Цилиндрическое зубчатое колесо имеет следующие конструктивные элементы:
Зубчатые колеса, у которых линия направления зуба параллельна оси колеса, называются прямозубыми.
Контакт пары зубьев цилиндрической прямозубой передачи происходит по линии параллельной оси.
ДЛИНА ЛИНИИ КОНТАКТА РАВНА ШИРИНЕ ВЕНЦА При работе прямозубой передачи пара зубьев входит в зацепление сразу по всей длине контакта, что сопровождается ударом зубьев и повышенным шумом. поэтому прямозубые передачи применяют при невысоких окружных скоростях.
ПЕРЕДАТОЧНОЕ ЧИСЛО: u = ω1/ω 2= n1/n 2 =d2/d 1= z2/z1 ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ ПРЯМОЗУБЫХ КОЛЕС
Раздел №2: Косозубые и шевронные передачи.
ОСОБЕННОСТИ КОСОЗУБЫХ ПЕРЕДАЧ: Косозубыми называются колеса, зубья которых наклонены к образующей цилиндра колеса на некоторый уголβ.
При работе косозубых колес зубья входят в зацепление не сразу по всей длине, а постепенно, что способствуют:  - плавной работе передачи - снижению динамических нагрузок - снижению шума Недостатком косозубых передач является наличие осевой линии, дополнительно нагружающей опоры валов. Для снижения осевых сил угол наклона линии зуба рекомендуют выполнять в пределах β = 8…20˚
ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ КОСОЗУБЫХ КОЛЕС
В косозубых колесах различают 2 шага зубьев:
- в нормальном сечении n-n нормальный шаг зубьев-pn -в торцовом сечении окружной шаг – pt Pt = P/cosβ
Следовательно модули у косозубых колес в разных сечениях будут разные.
нормальный модуль m = p/π
окружной модуль mt = pt/π mt = m/cosβ
делительный и начальный d = dw = mt z = mz/cosβ диаметры
ОСОБЕННОСТИ ШЕВРОННЫХ ПЕРЕДАЧ
Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с наклоненными на один угол в разные стороны зубьев, называется шевронными. В шевронной передаче осевые силы на полушевронах направлены в противоположные стороны, взаимно уравновешиваются и на опоры не передаются.
Раздел №3: Конические зубчатые передачи.
Конические зубчатые передачи применяют в передачах, когда геометрические оси валов пересекаются под углом Σ. Чаще всего Σ = 90˚.
КОНИЧЕСКИЕ КОЛЕСА БЫВАЮТ
с круговыми зубьями (точечный контакт в зацеплении)
. Шестерню в конической передаче часто располагают консольно. Аналогом начальных и делительных цилиндров цилиндрических зубчатых передач в конических передачах являются начальные и делительные конусы.
У конических колес высота, толщина зубьев и окружной шаг по длине зуба неодинаковы, поэтому различают 2 окружных модуля:
m- средний делительный окружной модуль(в среднем сечении) me- внешний делительный окружной модуль(на внешнем торце зуба)
средние делительные диаметры: d1 = mz1 гдеz1 и z2- числа зубьев шестерни и колеса d2 = mz2 внешние делительные диаметры: de1 = mez1 de2 = mez2 внешнее конусное расстояние: de = 0.5me√z1²+z2² среднее конусное расстояние: R = Re – 0.5b углы делительных конусов: шестерни-δ1 колеса-δ2 tg δ1 = z1/z2 δ2 = 90˚- δ1 передаточное число конической зубчатой передачи: u = ω1/ω2 = n1/n2 =z2/z1 = d2/d1 = de2/de1 = tgδ2 = 1/tgδ1 Вместо конических передач в машиностроении часто используют так называемые гипоидные передачи. Они предназначены для передачи вращения между перекрещивающимися геометрическими осями валов.
Раздел №4: Червячные передачи. Это передачи зацепления. Червячные передачи применяются для передачи вращающего движения между валами при угле перекрещивания их осей θ = 90˚.
Червячная передача – это зубчато-винтовая передача, движение в которой осуществляется по принципу винтовой пары.
ДОСТОИНСТВА ЧЕТВЯЧНОЙ ПЕРЕДАЧИ:
НЕДОСТАТКИ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ:
КЛАССИФИКАЦИЯ ЧЕРВЯЧНЫХ ПЕРЕДАЧ: (в зависимости от формы внешней поверхности червяка)
с глобоидным червяком (образующая- прямая линия). Имеет большую нагрузочную способность.
В зависимости от направления линии витка червяка:
В зависимости от расположения червяка относительно колеса:
с верхнем расположением червяка(допускают окружную скорость более 5м/c)
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 375. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 венец – часть зубчатого колеса, содержащая зубья
венец – часть зубчатого колеса, содержащая зубья



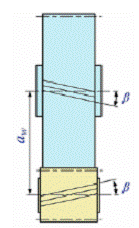 Профиль косого зуба в нормальном сечении n-n совпадает с профилем прямого зуба модуля m.
Профиль косого зуба в нормальном сечении n-n совпадает с профилем прямого зуба модуля m.

 Уравновешенность осевых сил у шевронных колес позволяет увеличить угол наклона зубьев до 40˚, что повышает нагрузочную способность и плавность работы передачи. Шевронные колеса применяются в быстроходных передачах высокой мощности.
Уравновешенность осевых сил у шевронных колес позволяет увеличить угол наклона зубьев до 40˚, что повышает нагрузочную способность и плавность работы передачи. Шевронные колеса применяются в быстроходных передачах высокой мощности.
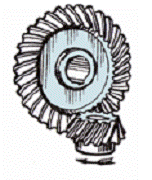
 с прямыми зубьями (линейный контакт в зацеплении)
с прямыми зубьями (линейный контакт в зацеплении) 
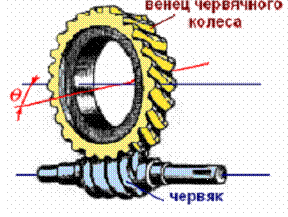 Червяк- это короткий винт с трапецеидальной нарезкой.
Червяк- это короткий винт с трапецеидальной нарезкой. с цилиндрическим червяком (образующая червяка- прямая линия).Такие червяки проще в изготовлении.
с цилиндрическим червяком (образующая червяка- прямая линия).Такие червяки проще в изготовлении.
 правое направление левое направление линии ветка
правое направление левое направление линии ветка линии витка
линии витка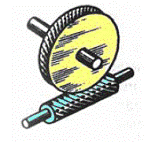 с нижним расположением червяка(при окружной скорости не более 5м/с)
с нижним расположением червяка(при окружной скорости не более 5м/с)
