Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ОСНОВНЫЕ ЭЛЕМЕНТЫ ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯКЛАССИФИКАЦИЯ ЗУБЧАТЫХ ПЕРЕДАЧ (в зависимости от конструктивного исполнения) 1.открытые передачи (зубья колес не защищены от внешней среды)
2.закрытые передачи
КЛАССИФИКАЦИЯ ЗУБЧАТЫХ ПЕРЕДАЧ (в зависимости от числаступеней) 1.одноступенчатые (одна пара колес в зацеплении)
2.многоступенчатые (две пары зубчатых колес в зацеплении и более)
1.эвольвентные (образующая профиля-эвольвента)
2.циклоидальные (образующая профиля-циклоида)
3.с зацеплением Новикова (образующая профиля-дуга окружности) Используются в высоконагруженных передачах,которые по конструктивным соображениям должны иметь малые габариты.
На практике в основном используют эвольвентный профиль зубьев, обеспечивающий их прочность, малые скорости скольжения в зоне зацепления и высокий КПД.
Изготовление зубчатых колес с эвольвентным профилем наиболее просто и дешево.
 Эвольвентой окружности называют кривую, которую описывает точка прямой, перекатывающаяся без скольжения по окружности.
ПОСТРОЕНИЕ ЭВОЛЬВЕНТЫ
Делительная окружность-это окружность, по которой толщина зуба колеса равна ширине впадины между зубьями.
Шаг зацепления ( p )-это расстояние между одноименными профилями двух смежных зубьев, измеренное по дуге делительной окружности.
Основной характеристикой зубчатого зацепления является модуль ( m )-линейная величина в π раз меньшая окружного шага зубьев pпо делительной окружности зубчатого колеса.
m = p/π С увеличением диаметра основной окружности db кривизна эвольвенты уменьшается и при db→ ∞ зубчатый профиль трансформируется в рейку с трапецеидальным профилем-основную рейку.
Профиль зуба основной рейки соответствует исходному контуру зубу, регламентированный стандартом. Этот контур положен в основу профилирования инструмента для нарезания зубьев.
ПАРАМЕТРЫ ИСХОДНОГО КОНТУРА
c*- коэф.радиального зазора для цилиндрических колес.c*=0.25
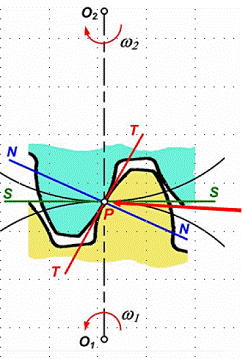
ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ УСЛОВИЯ ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯ.
Эвольвентные профили зубьев называются сопряженными, так как такой профиль обеспечивает постоянство передаточного числа зубчатой пары. В этом случае при вращении колес нормаль N-N в точке контакта профилей зубьев будет пересекать линию центров в одной и той же точке p - полюсе зацепления. Эта точка делит межосевое расстояние на части, обратно пропорц. угловым скоростям:
O1P/ O2P=ω2 /ω1
ОСНОВНЫЕ ЭЛЕМЕНТЫ ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯ Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения.
dw1 ,dw2-диаметры начальных окружностей шестерни и колеса;
aw-межосевое расстояние aw=(dw1+dw2) /2;
d1,d2-диаметры делительных окружностей шестерни и колеса; делительные и начальные окружности у колес совпадают, если (d1+d2)/2=aw ; ha-высота головки зуба шестерни и колеса;
hf-высота ножки зуба шестерни и колеса;
c-радиальный зазор в зацеплении шестерни и колеса;
da1,da2-диаметры окружностей вершин шестерни и колеса;
df1,df2-диаметры окружностей впадин шестерни и колеса;
p-окружной шаг;
s-окружная толщина зуба;
e-окружная ширина впадины зуба.
Для пары зубчатых колес, находящихся в зацеплении окружной шаг p, а следовательно и модуль m должны быть одинаковыми.
На делительной окружности толщина зуба равна ширине впадины: s =e Модуль зубьев- основной параметр зубчатых колес.
Все геометрические параметры зубчатых колес выражаются через модуль.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 324. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 (помещены в закрытые корпуса и работают в масляной ванне)
(помещены в закрытые корпуса и работают в масляной ванне)

 КЛАССИФИКАЦИЯ ЗУБЧАТЫХ ПЕРЕДАЧ (в зависимости от формы профиля зуба)
КЛАССИФИКАЦИЯ ЗУБЧАТЫХ ПЕРЕДАЧ (в зависимости от формы профиля зуба)

 Эвольвентное зацепление впервые было предложено Леонардом Эйлером в 1760 году.
Эвольвентное зацепление впервые было предложено Леонардом Эйлером в 1760 году. Окружность, по которой перекатывается прямая называется эволютойили основной окружностью, а перекатываемая прямая-производящей прямой.
Окружность, по которой перекатывается прямая называется эволютойили основной окружностью, а перекатываемая прямая-производящей прямой.

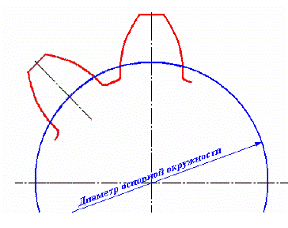

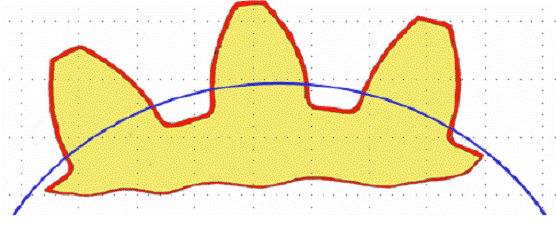

 шаг зубьев p=mπ, m-модуль зубчатого колеса
шаг зубьев p=mπ, m-модуль зубчатого колеса