
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Динамический метод наименьших квадратов (DOLS).Динамический метод наименьших квадратов для случайных процессов, являющихся интегрированными процессами первого порядка . План лекции
Текстовый материал лекции Напомним сначала некоторые определения и факты, излагавшиеся во второй части учебника. Пусть мы имеем N временных рядов Проблема, однако, в том, что у коинтегрированной системы I(1)рядов может быть несколько линейно независимых коинтегрирующих векторов. Если максимальное количество линейно независимых коинтегрирующих векторов для заданных рядов  Один из возможных вариантов выбора базисных коинтегрирующих векторов дается следующим представлением системы коинтегрированных I(1) рядов. Если ранг коинтеграции равен r , 0 < r < N , то при соответствующей перенумерации переменных система I(1) рядов
где C = (сi j) – матрица размера r ×(N – r), ut = (u1t , … , uN t)T – стационарный (в широком смысле) векторный случайный процесс с E(vt) = 0, ряды При этом уравнения y1 t = μ1 + c11 yr + 1, t +… + c1, N – r yN, t + u1 t . . . yr t = μr + cr 1 yr + 1, t + … + cr, N – r yN, t + ur t , представляют r коинтегрирующих регрессий, а векторы β(1) = (1, 0, 0, … , 0, – c11, … , – c1, N – r)T , β(2) = (0, 1, 0, … , 0, – c21, … , – c2, N – r)T , . . . β(r) = (0, 0, 0, … , 1, – cr 1, … , – cr, N – r )T образуют базис коинтеграционного пространства. Если ряды u1t , … , ur t не коррелированы с рядами ur + 1, t , … ,uN, t , то указанное выше представление называется треугольной системой Филлипса, и коинтегрирующие регрессии можно оценивать методом наименьших квадратов, получая при этом суперсостоятельные оценки коэффициентов. Однако в общем случае эти оценки не являются асимптотически нормальными, что затрудняет получение статистических выводов относительно истинных значений коэффициентов. Удачным исключением является здесь случай r = 1, когда имеется только одна коинтегрирующая регрессия
В этом случае условное распределение ОНК для коэффициентов (при фиксированных значениях y2,t , … , yN,t ) является асимптотически нормальным, и возможно использование стандартных процедур проверки гипотез о коэффициентах коинтегрирующего вектора, основанных на t- и F-статистиках (в асимптотическом плане), с коррекцией стандартных ошибок коэффициентов в случае, если ряд ut не является белым шумом. Коррекция состоит в замене стандартной оценки S2 дисперсии ряда ut состоятельной оценкой долговременной дисперсии этого ряда. Долговременная дисперсия ряда ut определяется соотношением и если выполнено условие
Если ut представляет собой процесс белого шума, то
т.е. долговременная дисперсия ряда ut совпадает с обычной дисперсией этого ряда. Если ut представляет собой стационарный процесс AR(1),
то так что
долговременная дисперсия равна где
Рассмотрим теперь следующую модель: где В этом случае так что объясняющая переменная Это осложнение преодолевается в процедуре динамического OLS (DOLS), разработанной в работах Phillips, Loretan (1991), Saikkonen (1991), Stock, Watson (1993). Статистическое моделирование показывает (Carrion-i-Silvestre and Sansó-i-Rosselló (2004)), что в малых выборках DOLS работает лучше чем еще одна модификация OLS (с теми же свойствами оптимальности) – FM OLS (Full Modified OLS).
В чем состоит идея DOLS? Рассмотрим ее на нашем примере. У нас так что Условное математическое ожидание случайной величины
Если обозначить то как при Запишем исходное уравнение в виде: т.е. или где Таким образом, в этой простейшей ситуации для предупреждения смещения OLS оценки коэффициента
В общем случае оценивается коинтеграционное уравнение
где ut =(u1t , u2t , ... , u N t)T – N-мерный гауссовский стационарный векторный ряд (теперь уже не обязательно N-мерный гауссовский белый шум), причем ряды u1t , ... , u N t могут быть коррелированнными между собой. (Гауссовость ряда ut означает, что совместное распределение значений ряда в любые T различных моментов времени является NT-мерным нормальным распределением.) При этом в правую часть приходится добавлять не только текущие, но также и запаздывающие (Lags) и опережающие (Leads) приращения переменных другое название метода – “Leads and Lags”): Разумеется, реально используется усечение бесконечной суммы в правой части, так что при этом получаем расширенное (по отношению к исходному) уравнение (DOLS-уравнение) Значение K должно быть достаточно большим для того, чтобы ликвидировать или свести к минимуму коррелированность объясняющих переменных с
Замечание Если Замечание Если
П р и м е р 5.1.1 Сгенерируем реализацию модели где Оценим уравнение
Кросс-коррелограмма рядов
(Заметим, что ряды значений В соответствии с видом кросс-коррелограммы, дополняем правую часть коинтеграционного уравнения текущим, двумя запаздывающими и двумя опережающими приращениями переменной
Сравним эти DOLS оценки коэффициентов c полученными ранее OLS оценками:
Качество DOLS оценок намного выше.
П р и м е р 5.1.2 Сгенерируем теперь реализацию модели где опять но на сей раз Поведение смоделированных реализаций мало отличается от предыдущих:
Оцениваем уравнение
Кросс-коррелограмма рядов
В соответствии с видом кросс-коррелограммы, опять дополняем правую часть коинтеграционного уравнения текущим, двумя запаздывающими и двумя опережающими приращениями переменной Оцениваем это уравнение:
Здесь в результате оценивания расширенного уравнения остается автокоррелированность в остатках, что можно учесть двумя способами.
Во-первых, можно применить для оценивания расширенного уравнения доступный вариант GLS или процедуру Кохрейна – Оркатта: этот вариант Сток и Ватсон называют DGLS (динамический обобщенный метод наименьших квадратов). Если, как в нашем примере, или то тогда надо взять ряд остатков Полученные оценки После этого производится авторегрессионное преобразование объясняющей и объясняющих переменных в расширенном уравнении, что приводит к преобразованному уравнению: В рамках преобразованного уравнения можно уже на законных основаниях проверять гипотезы о коэффициентах коинтеграционного соотношения, используя для этой цели t- и F-статистики. Применение указанного подхода в рамках процедуры, реализуемой в EViews (с AR(1) и AR(2)) приводит к следующим результатам:
Проверим гипотезу
Эта гипотеза не отвергается.
Если динамика ряда то можно не изменять спецификацию расширенного уравнения, производя авторегрессионное преобразование переменных, а вместо этого скорректировать надлежащим образом значения t- и F-статистик для проверки гипотез о значениях коэффициентов. При таком подходе в выражениях для t- и F-статистик несмещенная оценка где Стандартное выражение для t-статистики при проверке гипотезы Скорректированное значение равно Аналогично, скорректированное значение F-статистики равно
В нашем примере оценивание уравнения
Соответственно, отсюда находим: Скорректированное значение t-статистики для проверки гипотезы при этом гипотеза При проверке в DOLS уравнении совместной гипотезы ему соответствует P-значение 0.271, и при этом гипотеза
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 353. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
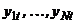 , каждый из которых является интегрированным порядка 1 (так что ряды
, каждый из которых является интегрированным порядка 1 (так что ряды  нестационарны, а ряды
нестационарны, а ряды  стационарны,
стационарны,  ). Если существует такой ненулевой вектор
). Если существует такой ненулевой вектор  , для которого
, для которого  – стационарный ряд, то говорят, что эти ряды коинтегрированы (в узком смысле); такой вектор
– стационарный ряд, то говорят, что эти ряды коинтегрированы (в узком смысле); такой вектор 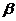 называется коинтегрирующим вектором.
называется коинтегрирующим вектором.  .
. равно r , то это число r называется рангом коинтеграции. Для коинтегрированной системы, состоящей из N рядов, ранг коинтеграции может принимать значения r = 1, … , N – 1. (Формально, если ряды не коинтегрированы, то r = 0. Если же имеется r = N линейно независимых коинтегрирующих векторов, то все N рядов стационарны.) Совокупность всех возможных коинтегрирующих векторов для коинтегрированной системы I(1) рядов образует r-мерное линейное векторное пространство, которое называют коинтеграционным пространством. Любой набор r линейно независимых коинтегрирующих векторов образует базис этого пространства, и если зафиксировать этот набор в качестве базиса, то тогда любой коинтегрирующий вектор является линейной комбинацией векторов, составляющих базис.
равно r , то это число r называется рангом коинтеграции. Для коинтегрированной системы, состоящей из N рядов, ранг коинтеграции может принимать значения r = 1, … , N – 1. (Формально, если ряды не коинтегрированы, то r = 0. Если же имеется r = N линейно независимых коинтегрирующих векторов, то все N рядов стационарны.) Совокупность всех возможных коинтегрирующих векторов для коинтегрированной системы I(1) рядов образует r-мерное линейное векторное пространство, которое называют коинтеграционным пространством. Любой набор r линейно независимых коинтегрирующих векторов образует базис этого пространства, и если зафиксировать этот набор в качестве базиса, то тогда любой коинтегрирующий вектор является линейной комбинацией векторов, составляющих базис.
 ,
, не коинтегрированы.
не коинтегрированы. .
.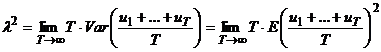 ,
, , то
, то  . Если исходить из того, что случайный процесс ut может быть аппроксимирован процессом MA(q) конечного порядка q , то в качестве оценки долговременной дисперсии можно взять оценку
. Если исходить из того, что случайный процесс ut может быть аппроксимирован процессом MA(q) конечного порядка q , то в качестве оценки долговременной дисперсии можно взять оценку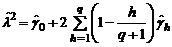 ,
, где
где  (
(  – остатки при OLS оценивании коинтегрирующей регрессии). Выбор q = O(T 1/5) обеспечивает состоятельность такой оценки для λ2.
– остатки при OLS оценивании коинтегрирующей регрессии). Выбор q = O(T 1/5) обеспечивает состоятельность такой оценки для λ2.  ,
, ,
,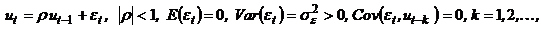

 ,
,
 ,
,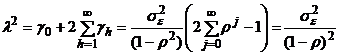 ,
,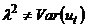 .
. 
 ,
, .
. ,
,  ,
, ~ i.i.d.
~ i.i.d.  ,
,  ~ i.i.d.
~ i.i.d.  ,
, 
 и
и  – I(1) переменные, но модель не является треугольной системой Филлипса из-за коррелированности
– I(1) переменные, но модель не является треугольной системой Филлипса из-за коррелированности  ,
, ,
,
 ~
~  , где
, где  .
. равно здесь:
равно здесь: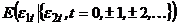 =
=  =
=  .
. ,
,
 , так и при
, так и при  .
. ,
,  ,
, ,
, , и теперь уже
, и теперь уже .
.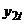 .
. , k =2, … , N,
, k =2, … , N, (отсюда
(отсюда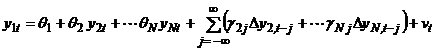 .
.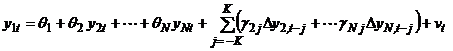 .
. , но и не излишне большим, поскольку это ведет к снижению эффективности оценок.
, но и не излишне большим, поскольку это ведет к снижению эффективности оценок. не является причиной по Грейнджеру для
не является причиной по Грейнджеру для  , то в правой части расширенного уравнения достаточно оставить только запаздывающие значения приращений:
, то в правой части расширенного уравнения достаточно оставить только запаздывающие значения приращений: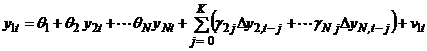 .
. , то для проверки гипотез о коэффициентах можно использовать стандартные процедуры, основанные на t - и F- статистиках (в этом случае DOLS оценки асимптотически нормальны). В противном случае для проверки линейных гипотез о коэффициентах следует использовать скорректированные F- и t-статистики с асимптотически оправданными F- и t-распределениями, предварительно заменив обычную оценку S2 для дисперсии vt на состоятельную оценку
, то для проверки гипотез о коэффициентах можно использовать стандартные процедуры, основанные на t - и F- статистиках (в этом случае DOLS оценки асимптотически нормальны). В противном случае для проверки линейных гипотез о коэффициентах следует использовать скорректированные F- и t-статистики с асимптотически оправданными F- и t-распределениями, предварительно заменив обычную оценку S2 для дисперсии vt на состоятельную оценку  “долговременной дисперсии” λ2 ряда vt . Последнее соответствует умножению обычной F-статистики на
“долговременной дисперсии” λ2 ряда vt . Последнее соответствует умножению обычной F-статистики на 
 .
.
 ,
,  ,
,
 ~ i.i.d.
~ i.i.d.  ,
,  – не коррелированные между собой гауссовские процессы белого шума.
– не коррелированные между собой гауссовские процессы белого шума.
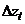 и
и  и
и  ,
,  ~ i.i.d.
~ i.i.d. 
 методом OLS по первым 30 наблюдениям:
методом OLS по первым 30 наблюдениям: .
. ,
,  , где
, где  ,
,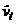 , полученных при оценивании расширенного уравнения (DOLS), и оценить уравнение
, полученных при оценивании расширенного уравнения (DOLS), и оценить уравнение 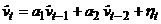 .
. и
и  используются для оценивания
используются для оценивания  :
: .
. .
. :
: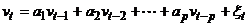 , (*)
, (*) дисперсии ошибок, вычисляемая по остаткам
дисперсии ошибок, вычисляемая по остаткам  и ряд остатков
и ряд остатков  , и в качестве оценки для
, и в качестве оценки для  берется
берется ,
, – оценка дисперсии ряда
– оценка дисперсии ряда  :
:  имеет вид
имеет вид  .
. .
. .
. ,
, 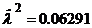 .
.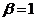 равно
равно ;
; вычисленное значение F-статистики равно 6.826679, что дает P-значение 0.005496 – эта гипотеза отвергается. Скорректированное значение F-статистики равно
вычисленное значение F-статистики равно 6.826679, что дает P-значение 0.005496 – эта гипотеза отвергается. Скорректированное значение F-статистики равно ,
,