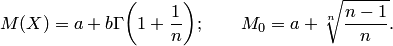Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Экспоненциальный закон распределенияНепрерывные случайные величины и некоторые законы их распределения Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток(интервал),называется непрерывной . Случайная величина
Функция
Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств
Рис.1 Так как
, то
Пример 1. Плотность распределения непрерывной случайной величины задана следующим образом:
Рис.2 Решение:
По формуле (1) находим функцию распределения F(x) для заданной случайной величины.
Если
Если
Если x>4, то
Итак,
Рис.3 Рассмотрим некоторые наиболее употребительные в инженерной практике законы распределения непрерывных случайных величин.  Нормальный закон распределения (закон Гаусса)
Кривая распределения изображена на рис.4. Она симметрична относительно точки
Рис.4 Рис.5
Нормальный закон распределения широко применяется в задачах практики. Укажем числовые характеристики нормально распределённой случайной величины (математическое ожидание и дисперсия):
Таким образом, параметры
Пример 2.
СВОЙСТВО: Если
ПРИМЕР 3. Случайная величина распределена нормально с параметрами
Экспоненциальный закон распределения
Основные характеристики (математическое ожидание и дисперсия) случайной величины
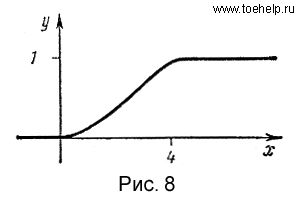
Кривая экспоненциального распределения вероятностей показана на рис.6, a, а график функции распределения
Рис.6,a рис.6,б Экспоненциальное (показательное) распределение часто используется в теории массового обслуживания (например, станции) и теории надёжности (например, Пример. Случайная величина Решение. По условию задачи математическое ожидание случайной величины
Распределение Вейбула Случайная величина
Математическое ожидание и мода случайной величины, распределённой по закону Вейбула, имеют следующий вид:
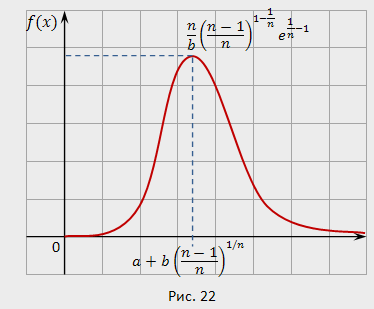
Кривая распределения Вейбула изображена на рис.7.
Рис.7 |
||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 244. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
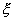 называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция*
называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* 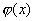 , удовлетворяющая для любых значений x равенству
, удовлетворяющая для любых значений x равенству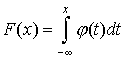
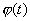 называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x1<x2, то на основании формулы (1) имеем
называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x1<x2, то на основании формулы (1) имеем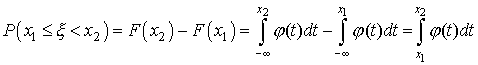
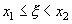 равна площади криволинейной трапеции с основанием [x1,x2], ограниченной сверху кривой
равна площади криволинейной трапеции с основанием [x1,x2], ограниченной сверху кривой 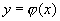 (рис.1).
(рис.1).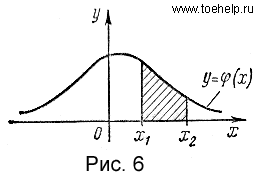
 , а на основании формулы (1)
, а на основании формулы (1) 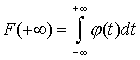
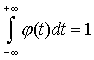
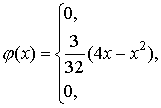
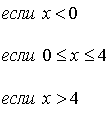
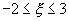 . Найти функцию распределения заданной случайной величины.
. Найти функцию распределения заданной случайной величины. 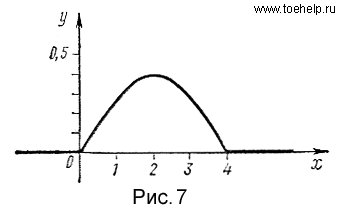
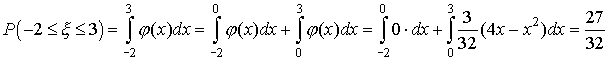
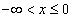 , то
, то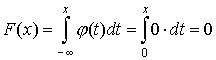
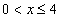 , то
, то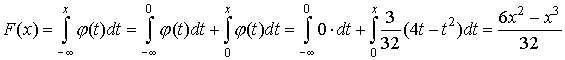
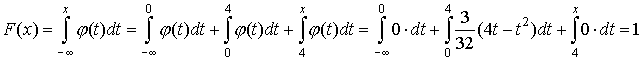
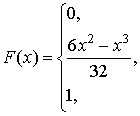
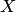 выражается формулой
выражается формулой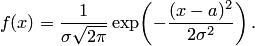
 (точка максимума). При уменьшении
(точка максимума). При уменьшении 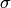 ордината точки максимума неограниченно возрастает, при этом кривая пропорционально сплющивается вдоль оси абсцисс, так что площадь под её графиком остаётся равной единицы (рис.5).
ордината точки максимума неограниченно возрастает, при этом кривая пропорционально сплющивается вдоль оси абсцисс, так что площадь под её графиком остаётся равной единицы (рис.5).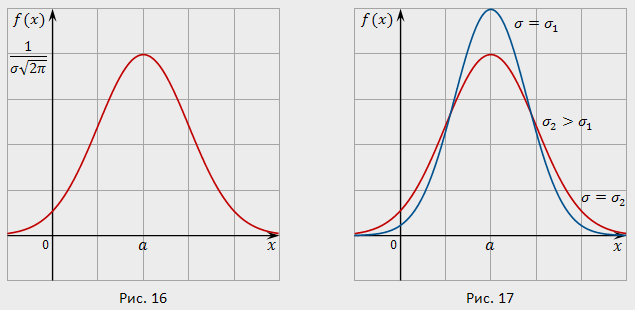

 и
и 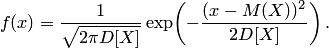 (3.1)
(3.1)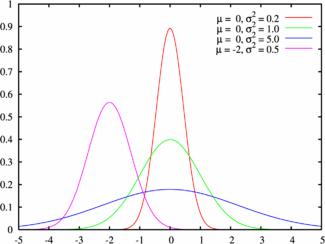

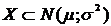 , то для нахождения вероятности попадания этой величины в заданный интервал (х1;х2) используется формула:
, то для нахождения вероятности попадания этой величины в заданный интервал (х1;х2) используется формула: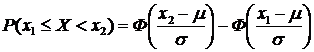 ,где Ф-значение функции распределения в указанной точке.
,где Ф-значение функции распределения в указанной точке.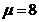 ,
, 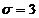 . Найти вероятность того, что случайная величина в результате опыта примет значение, заключенное в интервале (12,5; 14).
. Найти вероятность того, что случайная величина в результате опыта примет значение, заключенное в интервале (12,5; 14).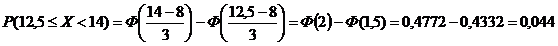
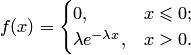
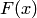 экспоненциального закона:
экспоненциального закона: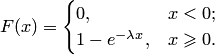

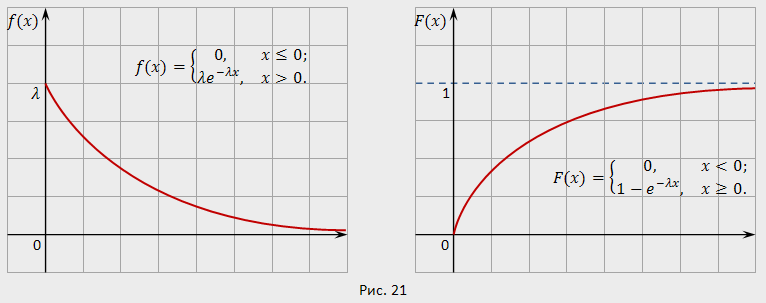
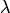 состоит в следующем:
состоит в следующем: 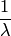 есть средний промежуток времени между двумя последовательными событиями.
есть средний промежуток времени между двумя последовательными событиями.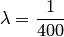 . Искомая вероятность есть
. Искомая вероятность есть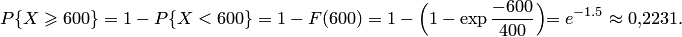
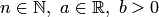 , если её плотность распределения вероятностей записывается в виде
, если её плотность распределения вероятностей записывается в виде