
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сортировка обменом (пузырьковая)Массив просматривается N-1 раз. При каждом просмотре сравниваются каждые два соседних элемента. Если элемент с меньшим индексом оказывается больше, производится их обмен. for i := 1 to n - 1 do for j := 1 to n - i do if a[j]>a[j+1] then begin (Обмен местами двух элементов, с номерами: j и (j+1).) endСортировка простыми вставками Сортировка методом прямого включения, так же, как и сортировка методом простого выбора, обычно применяется для массивов, не содержащих повторяющихся элементов. Сортировка этим методом производится последовательно шаг за шагом. На k-м шаге считается, что часть массива, содержащая первые k-1 элемент уже упорядочена, то есть С каждым шагом отсортированная часть массива увеличивается. Для выполнения полной сортировки потребуется выполнить n-1 шаг. Осталось ответить на вопрос, как осуществить поиск подходящего места для элемента х. Поступим следующим образом: будем просматривать элементы, расположенные левее х (то есть те, которые уже упорядочены), двигаясь к началу массива. Нужно просматривать элементы а[j], j изменяется от k-l до 1. Такой просмотр закончится при выполнении одного из следующих условий: • найден элемент а[j]<х, что говорит о необходимости вставки х между a[j-1] и a[j]; • достигнут левый конец упорядоченной части массива, следовательно, нужно вставить х на первое место.  До тех пор, пока одно из этих условий не выполнится, будем смещать просматриваемые элементы на 1 позицию вправо, в результате чего в отсортированной части будет освобождено место под х. На псевдокоде опишем фрагмент алгоритма сортировки с помощью прямого включения: For k := 2 to n do begin x := a[k]; j := k-1; { вставить х на подходящее место в a[1], …, a[k] } { для этого организуем цикл, которые выполняется, пока } { j > 0 и x <= a[j] } {в цикле смещаем элементы массива на 1 позицию вправо, а процесс) (уходит влево } {по выходу из цикла вставляем х в позицию j+1массива } end; Левый предел индекса можно ограничить установкой барьера(х). Тогда во внутреннем цикле проверку j>0 можно убрать: for k := 2 to n do begin х:=a[k]; a[0]:=х; {установка барьера} j:= k-1; while (a[j]>х) do begin{в цикле смещаем элементы массива на 1 позицию вправо, а процесс) (уходит влево } end; a[j+1]:=x; end;А Шелла. Существенными в сортировках вставками (или обмена) являются затраты на обмены или сдвиги элементов. Для их уменьшения желательно сначала производить погружение с большим шагом, сразу определяя элемент «по месту», а затем делать точную «подгонку». Так поступает сортировка Шелла: исходный массив разбивается на m частей, в каждую из которых попадают элементы с шагом m, начиная от 0,1,...,m-1 соответственно, то есть
0 , m , 2m , 3m ,... 1 , m+1, 2m+1, 3m+1,... 2 , m+2, 2m+2, 3m+2,... Каждая часть сортируется отдельно с использованием алгоритма вставок или обмена. Затем выбирается меньший шаг, и алгоритм повторяется. Шаг можно выбрать равным степени 2, например 64,32,16,8,4,2,1. Тогда на каждом следующем шаге происходит объединение каждых двух уже упорядоченных групп в одну. Сортировка Шелла требует трех вложенных циклов: по шагу сортировки (по уменьшающимся степеням 2 – m=64,32,16…), а затем два цикла обычной сортировки вставками для элементов группы, начинающейся с k с шагом m. Для двух последних циклов нужно взять базовый алгоритм, заменив шаг 1 на m и поменяв границы сортировки.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 296. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Далее необходимо взять k-й элемент и подобрать для него место в отсортированной части массива такое, чтобы после его вставки упорядоченность не нарушилась, то есть надо найти такое
. Далее необходимо взять k-й элемент и подобрать для него место в отсортированной части массива такое, чтобы после его вставки упорядоченность не нарушилась, то есть надо найти такое  что
что 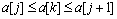 . Затем надо вставить элемент a[k] на найденное место.
. Затем надо вставить элемент a[k] на найденное место.