
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчёт ленточного фундамента на естественном основанииТребуется рассчитать фундамент под наружную стену жилого дома длиной L = 32,0 м. Нагрузка NOII = 738 кН/м. Пол подвала на 2,1 м ниже планировочной отметки земли. Геологические условия приняты по примеру раздела 3.1. Место строительства – г. Киров. Определяем глубину заложения подошвы фундамента. Из геологических условий (прорезка насыпного слоя) минимальная глубина заложения d = 1,0 м. Нормативная глубина промерзания супесей и суглинков вычисляется по формуле (2) [1] Значения температур для вычисления Mt определяем по табл. 1 [3].
Для супесей d01 = 0,28.
Ниже глубины 1 м залегают суглинки с d02 = 0,23, поэтому dfn необходимо уточнить по средневзвешенному значению d0 .
Расчётная глубина промерзания при kh = 0,7 (табл. 1 [1])
По табл. 2 [1] для суглинков с IL = 0,36 глубина заложения фундамента не менее df, то есть d = 1,3 м. При наличии подвала подошва фундамента должна располагаться ниже пола подвала не менее чем на 0,5 м, то есть d = 2,1 + 0,5 = 2,6 м. Из условия размещения фундаментной подушки высотой 0,5 м, блоков стен подвала высотой 0,6 и 0,3 м и армированного пояса толщиной 0,1 м окончательно принимаем d = 3 × 0,6 + 0,3 + 0,5 + 0,1 = 2,7 м, то есть подошва фундамента находится на отметке –3,200 (рис. 1). Принимаем db = 2 м, так как глубина подвала 2,1 > 2 м (см. пояснения к формуле (7) [1]). Для суглинка j =24°, с =20 кПа, gII =21,0 кН/м3, IL = 0,36. По табл. 4 [1] имеем Mg = 0,72; Mq = 3,87; Mc = 6,45. По табл. 3 [1] принимаем при 0,25 < IL £ 0,5 и L/H < 1,5 gС1 = 1,2; gС2 =1,1. k = 1; kz = 1.
 м. м.
Определяем расчётное сопротивление грунта при ширине фундамента b = 1 м по формуле (7) [1]
Вычисляем требуемую площадь фундамента при gmt = 20 кН/м3 
Принимаем фундаментные подушки ФЛ 20.12-3 (b = 2,0 м) и стеновые блоки ФБС 24.5.6-Т(п). При b = 2,0 м
Определяем вес 1 п. м фундамента и грунта на его уступах
Расчётная нагрузка по подошве фундамента
Среднее давление под подошвой фундамента
СНиП 2.02.01-83 (п. 2.45) рекомендует применять прерывистые фундаменты. При этом R определяется как для непрерывного фундамента с повышением его значения на коэффициент kd. По табл. 5 [1] для суглинка с IL = 0,36 принимаем kd = 1,1. Площадь подошвы ленточного фундамента длиной L = 32 м, подлежащего замене на прерывистый фундамент, A = L×b = 32× 2 = 64 м2. Площадь всех блоков Выбираем по каталогу размер подушки (как правило, bпр > b). Проверим три варианта: а) bпр = 2,0 м; б) bпр = 2,4 м; в) bпр = 2,8 м. Длина блоков l = 1,18 м. Площади подошвы одного блока соответственно: а) A ¢пр = 2,36 м2; б) A ¢пр = 2,83 м2; в) A ¢пр = 2,83,33 м2. Определяем число необходимых блоков а) где Dn – поправка для округления отношения Aпр / A ¢пр до большего целого числа. Фактическая величина а) в) Находим величину просвета между блоками а) в) Наиболее экономичное решение при использовании блоков ФЛ 28.12-3 в количестве 18 штук, которые устанавливаются с зазором 63 см. Требуется проверка прочности подстилающего слоя основания, так как ниже залегает слой супеси с меньшим R. Пример расчёта приводится в разделе 3.4. Определяем стоимость устройства 1 п. м фундамента по укрупнённым единичным расценкам.
Таблица 3 Стоимость устройства 1 п. м ленточного фундамента
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 563. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 .
. .
. м.
м.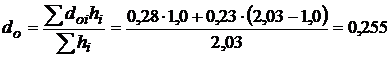 ;
; м.
м.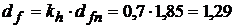 м.
м. .
.
 кПа.
кПа. м2.
м2.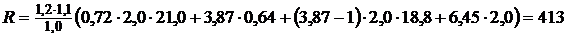 кПа.
кПа.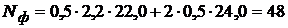 кН/м;
кН/м; кН/м.
кН/м. кН/м.
кН/м. .
. м2.
м2. :
: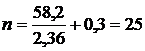 ; б)
; б)  ; в)
; в)  ,
,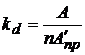 :
: ; б)
; б)  ;
; .
. :
: м; б)
м; б)  м;
м;  м.
м.