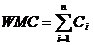Набор метрик Чидамбера и Кемерера

В 1994 году С. Чидамбер и К. Кемерер (Chidamber и Кетегег) предложили шесть проектных метрик, ориентированных на классы [24]. Класс — фундаментальный элемент объектно-ориентированной (ОО) системы. Поэтому измерения и метрики для отдельного класса, иерархии классов и сотрудничества классов бесценны для программного инженера, который должен оценить качество проекта.

Набор Чидамбера-Кемерера наиболее часто цитируется в программной индустрии и научных исследованиях. Рассмотрим каждую из метрик набора.

Метрика 1: Взвешенные методы на класс WMC (Weighted Methods Per Class)

Допустим, что в классе С определены п методов со сложностью с₁..._,c₂,..., с_n. Для оценки сложности может быть выбрана любая метрика сложности (например, цикломатическая сложность). Главное — нормализовать эту метрику так, чтобы номинальная сложность для метода принимала значение 1. В этом случае

Количество методов и их сложность являются индикатором затрат на реализацию и тестирование классов. Кроме того, чем больше методов, тем сложнее дерево наследования (все подклассы наследуют методы их родителей). С ростом количества методов в классе его применение становится все более специфическим, тем самым ограничивается возможность многократного использования. По этим причинам метрика WMC должна иметь разумно низкое значение.

Очень часто применяют упрощенную версию метрики. При этом полагают С_i= 1, и тогда WMC — количество методов в классе.

Оказывается, что подсчитывать количество методов в классе достаточно сложно. Возможны два противоположных варианта учета.

1. Подсчитываются только методы текущего класса. Унаследованные методы игнорируются. Обоснование — унаследованные методы уже подсчитаны в тех классах, где они определялись. Таким образом, инкрементность класса — лучший показатель его функциональных возможностей, который отражает его право на существование. Наиболее важным источником информации для понимания того, что делает класс, являются его собственные операции. Если класс не может отреагировать на сообщение (например, в нем отсутствует собственный метод), тогда он пошлет сообщение родителю.

2. Подсчитываются методы, определенные в текущем классе, и все унаследованные методы. Этот подход подчеркивает важность пространства состояний в понимании класса (а не инкрементности класса).

Существует ряд промежуточных вариантов. Например, подсчитываются текущие методы и методы, прямо унаследованные от родителей. Аргумент в пользу данного подхода — на поведение дочернего класса наиболее сильно влияет специализация родительских классов.

На практике приемлем любой из описанных вариантов. Главное — не менять вариант учета от проекта к проекту. Только в этом случае обеспечивается корректный сбор метрических данных.

Метрика WMC дает относительную меру сложности класса. Если считать, что все методы имеют одинаковую сложность, то это будет просто количество методов в классе. Существуют рекомендации по сложности методов. Например, М. Лоренц считает, что средняя длина метода должна ограничиваться 8 строками для Smalltalk и 24 строками для C++ [45]. Вообще, класс, имеющий максимальное количество методов среди классов одного с ним уровня, является наиболее сложным; скорее всего, он специфичен для данного приложения и содержит наибольшее количество ошибок.