
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Способы тестирования условий
Цель этого семейства способов тестирования — строить тестовые варианты для проверки логических условий программы. При этом желательно обеспечить охват операторов из всех ветвей программы. Рассмотрим используемую здесь терминологию. Простое условие — булева переменная или выражение отношения. Выражение отношения имеет вид Е1 <оператор отношения> E2, где El, Е2 — арифметические выражения, а в качестве оператора отношения используется один из следующих операторов: <, >, =, Составное условие состоит из нескольких простых условий, булевых операторов и круглых скобок. Будем применять булевы операторы OR, AND (&), NOT. Условия, не содержащие выражений отношения, называют булевыми выражениями. Таким образом, элементами условия являются: булев оператор, булева переменная, пара скобок (заключающая простое или составное условие), оператор отношения, арифметическое выражение. Эти элементы определяют типы ошибок в условиях. Если условие некорректно, то некорректен по меньшей мере один из элементов условия. Следовательно, в условии возможны следующие типы ошибок: q ошибка булева оператора (наличие некорректных / отсутствующих / избыточных булевых операторов); q ошибка булевой переменной; q ошибка булевой скобки; q ошибка оператора отношения; q ошибка арифметического выражения. Способ тестирования условий ориентирован на тестирование каждого условия в программе. Методики тестирования условий имеют два достоинства. Во-первых, достаточно просто выполнить измерение тестового покрытия условия. Во-вторых, тестовое покрытие условий в программе — это фундамент для генерации дополнительных тестов программы.  Целью тестирования условий является определение не только ошибок в условиях, но и других ошибок в программах. Если набор тестов для программы А эффективен для обнаружения ошибок в условиях, содержащихся в А, то вероятно, что этот набор также эффективен для обнаружения других ошибок в А. Кроме того, если методика тестирования эффективна для обнаружения ошибок в условии, то вероятно, что эта методика будет эффективна для обнаружения ошибок в программе. Существует несколько методик тестирования условий. Простейшая методика — тестирование ветвей. Здесь для составного условия С проверяется: q каждое простое условие (входящее в него); q Тruе-ветвь; q False-ветвь. Другая методика — тестирование области определения. В ней для выражения отношения требуется генерация 3-4 тестов. Выражение вида Е1 <оператор отношения> Е2 проверяется тремя тестами, которые формируют значение Е1 большим, чем Е2, равным Е2 и меньшим, чем Е2. Если оператор отношения неправилен, а Е1 и Е2 корректны, то эти три теста гарантируют обнаружение ошибки оператора отношения. Для определения ошибок в Е1 и Е2 тест должен сформировать значение Е1 большим или меньшим, чем Е2, причем обеспечить как можно меньшую разницу между этими значениями. Для булевых выражений с п переменными требуется набор из 2n тестов. Этот набор позволяет обнаружить ошибки булевых операторов, переменных и скобок, но практичен только при малом п. Впрочем, если в булево выражение каждая булева переменная входит только один раз, то количество тестов легко уменьшается. Обсудим способ тестирования условий, базирующийся на приведенных выше методиках. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 370. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
, 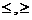 .
.