Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Приближенное вычисление функций вMATLAB.Полиномы от одной переменной имеют в MATLAB два разных представления – в виде вектора-строки из числовых коэффициентов и символьное. Например, полиному Пример: %%%%%%%%%% poly2sym([-2 0 1 -1]) ans = - 2*x^3 + x - 1 %%%%%%%%%% %объявление символьной переменной x symsx; sym2poly(-2*x.^3+x-1) ans = -2 0 1 -1 %%%%%%%%%%
Для вычисления значения полинома применяется функция polyval, реализующая схему Горнера: y=polyval(p,x); где p – вектор коэффициентов, расположенных в порядке убывания степени x; x – значение аргумента; y – значение полинома.
Пример: вычислим значение полинома p(x)=3x2+2x+1 в точке x=5 %%%%%%%%%%%%% p=[3 2 1]; y=polyval(p,5) y = 86 %%%%%%%%%%%%%
Пример: Функция V=vander(x) возвращает матрицу Вандермонда порядка length(x), j-й столбец которой определяется: V(:, j)=xn-j. Если: %%%%%%%%%%%%% x=[1 2 3 4]; V=vander(x) V = 1 1 1 1 8 4 2 1 27 9 3 1 64 16 4 1 %%%%%%%%%%%%% Пояснение:
Пример: Построим интерполяционные полиномы согласно решению системы уравнений (*) в двух частных случаях для числа узлов интерполяции соответственно 6 и 10.
% Полиномиальная интерполяция % определим вектор узлов интерполяции x=[0 0.1 0.3 0.6 0.7 0.9 1]; % определим значения интерполируемой функции, % считая эти значения случайными величинами,  % распределенными по нормальному закону y=[]; fori=1:length(x) y=[y;randn]; end % решаем систему уравнений 2.17 и находим % вектор-столбец коэффициентов полинома a=vander(x)\y; % строим интерполирующую функцию xv=-0.01:0.01:1.01; phi=polyval(a,xv); % строим график интерполирующей функции. % а маркерами метим значения функции % в узлах интерполяции plot(x,y,'*',xv,phi);
% Полиномиальная интерполяция % определим вектор узлов интерполяции x=[0 0.1 0.3 0.6 0.7 0.9 1]; % определим значения интерполируемой функции, % считая эти значения случайными величинами, % распределенными по нормальному закону y = 2*x.^2+5*x+2 % решаем систему уравнений 2.17 и находим % вектор-столбец коэффициентов полинома a=vander(x)\y'; % строим интерполирующую функцию xv=-0.01:0.01:1.01; phi=polyval(a,xv); % строим график интерполирующей функции. % а маркерами метим значения функции % в узлах интерполяции plot(x,y,'*',xv,phi);
%Интерполяция с помощью сплайна %определим вектор узлов интерполяции x=0:0.025:1; %определим значения интерполируемой функции, %считая эти значения случайными величинами, %распределенными по нормальному закону y=[]; fori=1:length(x) y=[y randn]; end %вводим сетку на отрезке интерполяции xv=0:0.001:1.0; %обращаемся к стандартной процедуре MATLAB yv=interp1(x,y,xv, 'spline'); %рисуем сплайн plot(x,y,'*',xv,yv); Пример: Используя метод наименьших квадратов в MATLAB. %%%%%%%%%%%%%%%%%%%%%%%%%%%% % задаем числовые значения x и y x=[0 1 2 3 4 5]; y=[2.8 6.1 10.9 18.1 27.3 38]; p1=polyfit(x,y,1) p2=polyfit(x,y,2) % для визуализации графиков этих полиномов следует % найти их значения в промежуточных точках на интервале: xx=linspace(min(x), max(x), 100); % вычислим в этих xx значения полиномов p1 и p2 % при помощи функции polyval и запишем вектора yy yy1=polyval(p1,xx); yy2=polyval(p2,xx); % для наглядности построим графики полиномов %и разместим заданные массивами x и y круглыми маркерами % также сделаем надпись % plot(x,y, 'o', xx, yy1, xx, yy2) hold on; plot(x, y, 'o '); hold on; plot(xx, yy1, 'g'); hold on; plot(xx, yy2,'r'); legend('DATA', '{\itp}^{(1)}({\itx})', '{\itp}^{(2)}({\itx})') %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Пример: В Matlab есть стандартные средства дифференцирования - diff(x). Она принимает аргумент x, который является массивом. Методы численного дифференцирования применяются, если исходную функцию y(x) трудно или невозможно продифференцировать аналитически. Методы имеют разную погрешность при расчётах. % определим шаг сетки h=0.2; % интервал значений x x=0:h:pi; % число необходимых итераций n=length(x); % значение производной y=sin(x) dy=cos(x); dz=sin(x) % нахождение производной правой конечной разностью (2.62) fori=1:(n-1) dy1(i)=(sin(x(i+1))-sin(x(i)))/h; er1(i)=abs(dy(i)-dy1(i)); end % нахождение производной левой конечной разностью (2.61) fori=2:n dy2(i)=(sin(x(i))-sin(x(i-1)))/h; er2(i)=abs(dy(i)-dy2(i)); end % нахождение производной центральной конечной разностью (2.63) fori=2:(n-1) dy3(i)=(sin(x(i+1))-sin(x(i-1)))/(2*h); er3(i)=abs(dy(i)-dy3(i)); end % отображение plot(x([1:(n-1)]),er1([1:(n-1)]),'-o', x([2:n]),er2([2:n]),'-p', x([2:(n-1)]),er3([2:(n-1)]),'-h');
title('Погрешность ("разность" анлитического и численного решения)'); legend('Правая', ' Левая', 'Центральная')
grid on; figure; plot(x([1:(n-1)]),dy([1:(n-1)]),'-d', x([1:(n-1)]),dy1([1:(n-1)]),'-o'); legend('cos(x)', 'производная по правой конечной разности') gridon
Пример: Вычислить определенный интеграл в диапазоне от 1 до 10 с шагом 0,5 для заданной функции: а) методом трапеций: x=1:0.01:10; y=x.^3 +2*x.^2+1; trapz(y)
б) методом Симпсона quad('x.^3 +2*x.^2+1',1,10,0.1)
symsx P=x^3+2*x^2+1; int(P,1,10)
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 184. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
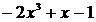 соответствуют: вектор коэффициентов [-2 0 1 -1] или [-2, 0, 1, -1], символьное выражение -2*x.^3+x-1. Для преобразования из одного формата представления полинома в другой используются функции poly2sym(для перехода от вектора коэффициентов к символьному представлению) и sym2poly(для перехода от символьного представления к вектору коэффициентов).
соответствуют: вектор коэффициентов [-2 0 1 -1] или [-2, 0, 1, -1], символьное выражение -2*x.^3+x-1. Для преобразования из одного формата представления полинома в другой используются функции poly2sym(для перехода от вектора коэффициентов к символьному представлению) и sym2poly(для перехода от символьного представления к вектору коэффициентов).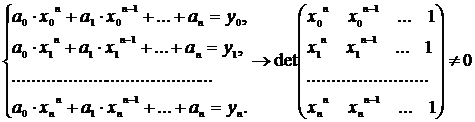 (*)
(*)