
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Исходные соотношения строгой электродинамической теорииСодержание Введение……………………………………………………………………………...3 Исходные соотношения электродинамической теории…………………………...5 Волны Е-типа в ассиметричном планарном диэлектрическом волноводе……....9 Решение задач………………………………………………………………………16 Источники и литература…………………………………………………………...21
ВВЕДЕНИЕ Устойчивой тенденцией развития современной радиоэлектроники является освоение все более коротких диапазонов длин волн (λ): миллиметровых λ = 10…1 мм (f = 30…300 ГГц) и оптических λ = 1000…0,001 мкм (f = 3 . 10 11...3 . 10 16 Гц). Линии передач (ЛП) предназначены для переноса электромагнитной энергии на расстояния. Они входят в состав различных устройств (фильтров, направленных ответвителей, делителей, фазовращателей, вентилей и т.п.). Перед разработчиками линий передачи ставятся довольно противоречивые задачи: ЛП должны обеспечивать малые потери энергии, большую передаваемую мощность, иметь малые габариты и массу, обладать высокой технологичностью и устойчивостью к внешним воздействиям. К этим требованиям добавляются широкополосность, лёгкость изгиба линии передачи при минимальных потерях, удобство подключения активных элементов, отсутствие излучения, невосприимчивость к внешним помехам, удобство управления электромагнитным полем в линии стыковки с другими ЛП, стоимость. Важным является также наличие надежной и подтверждаемой экспериментом теории и расчетного аппарата. На более длинных диапазонах (чем миллиметровые и оптические) волн с успехом используются ЛП в виде металлических волноводов различных сечений, полосковые и микрополосковые линии и т.п.  Диэлектрические волноводы (ДВ) применяются в диапазоне миллиметровых волн, при этом используется достаточно широкая номенклатура материалов: полиэтилен (ε = 2), кремний (ε = 2,5), поликор (ε = 12…14). Достигнутая величина потерь составляет 0,1…0,15 дБ/см при f = 100 Гц. Диэлектрические волноводы наиболее широко используются в устройствах интегральной оптики. Планарный диэлектрический волновод представляет собой нанесённую на подложки полоску тонкой плёнки, показатель преломления n2 которой больше показателей преломления n3 подложки и покрытия n1 (если покрытие отсутствует, то n1 = n0). Если n1 = n3, то волновод называется симметричным, в противном случае – ассиметричным. Поскольку планарный волновод «удерживает» поле только в одном измерении, для создания ряда устройств используют полосковые (двумерные) структуры. Диэлектрические волноводы широко используются в интегральной оптике для построения делителей, фильтров направленных ответвителей, модуляторов, переключателей, детекторов, тонкоплёночных лазеров и др., а также волоконно-оптических линиях связи (ВОЛС), в функциональных узлах оптоэлектронных устройств, осуществляющих обработку информации, в голографических системах и т.п. Основные свойства ДВ можно рассмотреть на бесконечной в одном направлении модели плоской пластины, т.е. планарного ДВ. В то же время планарный ДВ, представляя собой практический интерес, относительно просто анализируется как методом лучевой оптики, так и с помощью решения уравнений Максвелла.
Исходные соотношения строгой электродинамической теории Пленочные диэлектрические волноводы имеют некоторые общие черты с полыми неметаллическими волноводами (в частности, и те и другие могут поддерживать ограниченное число направленных типов волн (мод) на любой заданной частоте; в обеих структурах возможно преобразование мод, если форма волновода отклоняется от идеальной прямолинейной). Исследуем направляемые (волноводные) моды на примере планарного регулярного диэлектрического волновода (рис. 1).
Y
“ “ “ “ “ “ n1“ “ “ “ “ “ “
t n2 Z
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ n3 ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Рис. 1. X Для простоты далее будем полагать, что волновод является бесконечно протяженным в направлении оси Y и изменения поля в этом направлении нет, d/dy=0. Ограничимся случаем монохроматического поля с временной зависимостью eiwt, где w- круговая частота. Для определения структуры электромагнитного поля волн диэлектрического волновода необходимо решить систему уравнений Максвелла:
rotH = iweаE 1. rotE = -iwmaH,
где Е = Еmеiwt и Н = Нmеiwt , eа,mа – абсолютная диэлектрическая и магнитная проницаемость с граничными условиями на поверхности раздела х=0, х=t и физическим условием убыванием поля при х ® ± ¥.
Раскроем соотношение (1):
rotH= d/dx d/dy d/dz = x0(dHz/dy-dHy/dz) - y0(dHz/dx-dHx/dz) + Hx Hy Hz + z0(dHy/dx-dHx/dy) =iwea(x0Ex+y0Ey+z0Ez)= =x0iweaEx+y0iweaEy+ z0iweaEz ;
rotE= d/dx d/dy d/dz = x0(dEz/dy-dEy/dz) - y0(dEz/dx-dEx/dz) + Ex Ey Ez + z0(dEy/dx-dEx/dy) =-iwma(x0Hx+y0Hy+z0Hz)= =x0iwmaHx+y0iwmaHy+ z0iwmaHz ; Если векторы равны, то равны их соответствующие компоненты. Следовательно мы можем записать:
dHz/dy – dHy/dz = iweaEx 2. dHx/dz – dHz/dx = iweaEy dHy/dx – dHx/dy = iweaEz ;
dEz/dy – dEy/dz = iwmaHx 3. dEx/dz – dEz/dx = iwmaHy dEy/dx – dEx/dy = iwmaHz ;
Поскольку в направляющих линиях необходимо передавать энергию из одного сечения в другое, то аналогично случаю полных металлических волноводов решение (2), (3) в диэлектрическом волноводе ищем в виде бегущих в направлении оси zволн:
4. E=E(x)e-iGz=Em(x)ei(wt-Gz) H=H(x)e-iGz=Hm(x)ei(wt-Gz)
где Em(x), Hm(x) –комплексные амплитуды, зависящие только от x, (d/dy=0). G - коэффициент распространение волны в рассматриваемой структуре. Учитываяd/dy=0, подставим (4) в (2) и (3):
1) dHz/dy-dHy/dz=-dHy\dz=-dHmyei(wt-Gz)/dz=-Hmyei(wt-Gz) (-iG)=iweaEmxei(wt-Gz) GHmy=weaEmx ; 2) dHx/dz-dHz/dx=dHmxei(wt-Gz)/dz-dHmzei(wt-Gz)/dx=Hmxei(wt-Gz) (-iG) - Hmz/dx* *ei(wt-Gz)=iweaEmyei(wt-Gz) -iGHmx –dHmz/dx=iweaEmy 3) dHy/dx – dHx/dy=dHy/dx=dHmyei(wt-Gz)/dx=dHmy/dx ei(wt-Gz)=iweaEmzei(wt-Gz) dHmy/dx=iweaEmz 4) dEz/dy-dEy/dz=-dEy/dz=-dEmyei(wt-Gz)/dz=-Emyei(wt-Gz) (-iG)=-iwmaHmxei(wt-Gz) GEmy=-wmaHmx 5) dEx/dz-dEz/dx=dEmxei(wt-Gz)/dz-dEmzei(wt-Gz)/dx=Emxei(wt-Gz) (-iG)–dEmzei(wt-Gz) =-iwmaHmyei(wt-Gz) -iGEmx - dEmz/dx= -iwmaHmy 6) dEy/dx-dEx/dy=dEmyei(wt-Gz)/dx=dEmy/dx ei(wt-Gz)=-iwmaHmzei(wt-Gz) dEmy/dx=-iwmaHmz Таким образом, получим 2 подсистемы:
Для H-мод -iGHmx - dHmz/dx=iweaEmy 5. GEmy= - wmaHmx Hmz¹0; Emz=0 dEmy/dx=-imaHmz;
6. GHmy=weaEmx Emz¹0; Hmz=0 dHmy/dx=iweaEmz ;
Из (5), (6) следует, что для рассматриваемого случая моды делятся на волны типа H: (Emz=0; Hmz¹0), определяемые уравнениями (5), для которых отличны от нуля только составляющие Emy, Hmx, Hmzи на волны типа E: (Hmz=0: Emz¹0),определяемые уравнениями (6), для которых отличны от нуля только составляющие Hmy, Emx, Emz.Таким образом, для определения возможных типов волн в диэлектрическом плёночном волноводе достаточно найти продольную Hmz – компоненту для Н – волн или Emz – компоненту для Е – волн. Каждая из компонент электромагнитного поля в каждой точке из областей на рисунке 1 удовлетворяет однородному волновому уравнению:
Ñ2 Em + ko2 en Em = 0 7. Ñ2 Hm + ko2 en Hm = 0 ;
соответствующим граничным условиям на поверхности раздела (x=0, t) и условию убывания при x®+_¥; полагалось m1=m2=m3=m0. В (7) k0=2p/l0- -волновое число свободного пространства (l0 – длинна волны); Ñ2=d2/dx2+d2/dy2+d2/dz2 - оператор Лапласа; en=eаn.e0 ( где n=1, 2, 3…) – относительная диэлектрическая проницаемость сред. Докажем 1-е уравнение в (1). Возьмём ротор правой части и от левой части 1-ого уравнения в системе (1): rot rotH=iwearotE;
Левая часть этого уравнения есть:
rot rotH=grad divH - Ñ2H;
Так как по 3-му уравнению электродинамики divB=divmaH=0 то отсюда следует,что divH=0. Подставляя это в предыдущее уравнение, в результате получим : Ñ2 H + k2 H = 0,где k2=w2eama; Ñ2 Hm ei(wt-Gz) + k02 e Hm ei(wt-Gz) = 0; Ñ2 Hm + k02 e Hm = 0;
То есть мы получили 1-ое уравнение в системе (7). Докажем теперь 2-ое уравнение в (7). Берем ротор от левой и правой частей 2-ого уравнения в системе (1):
rot rotE=-iwmarotH;
Левая часть этого уравнения есть:
rot rotE=grad divE - Ñ2E;
По 4-ому уравнению электродинамики diveaE=divD=r. Так как мы рассматриваем идеальные условия, то r=0. Получаем:
Ñ2E + k2E=0; Ñ2 Em ei(wt-Gz) + k02 e Em ei(wt-Gz) = 0; Ñ2Em + k02e Em=0; То есть получили 2-ое уравнение в системе (7). Волны E – типа в асимметричном планарном диэлектрическом волноводе Сейчас и в дальнейшем будем исследовать только Е-моды в диэлектрическом планарном волноводе. Из уравнений (5), (6) видно, что для определения структуры электромагнитных волн в диэлектрическом волноводе удобно использовать компоненты Emyдля H - волн и Hmy для E – волн, так как при выражении через них других компонент нужно брать производную, а это проще, чем брать интеграл при выражении компонент через Emz, Hmz. Для нахождения составляющих Hmy, Еmх, Еmz волн Е-типа, мы будем использовать систему уравнений (6). Непосредственно из (7) для каждой из сред на рисунке 1 получим систему уравнений:
8а. d2[H(2)]my/dx2 + h2 [H(2)]my=0 при 0 £ x £ t; где h2=k22-G2=k02e2-G2
8б. d2[H(1)]my/dx2 - q2 [H(1)]my=0 при x < 0 ; где q2=G2- k12=G2- k02e1
8в. d2[H(3)]my/dx2 - p2 [H(3)]my=0 при x > t; где p2=G2- k32=G2- k02e3
Отличие записи уравнений (8а) от (8б), (8в)обусловлено тем, что электромагнитные волны, определяемые вне диэлектрического слоя 0 £ x £ t, должны иметь характер поверхностной волны, то есть поле как бы “прилипает” к поверхности раздела x=0, t и амплитуда уменьшается при удалении от неё по экспоненциальному закону. Величины h, p, q при записи (8а), (8б), (8в) вещественно положительные числа. На границе раздела x=0, t (рисунок 1) тангенциальные составляющие электрического и магнитного поля должны удовлетворять граничным условиям:
[H(1)]my | x=0 = [H(2)]my | x=0; [H(2)]my | x=t = [H(3)]my | x=t; 9. [E(1)]mz | x=0 = [E(2)]mz | x=0; [E(2)]mz | x=t = [E(3)]mz | x=t;
(10) находим из (8а), (8б), (8в). Для первой среды:
d2[H(1)]my/dx2 - q2 [H(1)]my=0; l2 - q2 = 0 ; l1,2= ± q; [H(1)]my=AEeqx – C1e-qx;
Из физического условия убывания поля при x®-¥ следует С1=0.
Для второй среды:
d2[H(2)]my/dx2 + h2 [H(2)]my=0; l2 + h2 = 0 ; l1,2= ± ih; [H(2)]my=Beihx – Ce-ihx;
Для третьей среды:
d2[H(3)]my/dx2 - p2 [H(3)]my=0; l2 - p2 = 0 ; l1,2= ± q; [H(3)]my=De-p(x-t) + C2ep(x-t); Из физического условия убывания поля при x®+¥следует C2=0. Сдвиг на t в показателе экспоненты возникает, потому что третья среда имеет уравнение x ³ t.
AEeqx при x < 0;
10. Hmy= Beihx+Ce-ihx при 0 £ x £ t;
De-p(x-t) при x > t; где AE, B, C, D, q, h, p – постоянные, которые нужно определить.
Из граничных условий для Hmy в (9) получаем соотношения: а)используя граничное условие [H(1)]my | x=0 = [H(2)]my | x=0, получаем AE eq0 = B eih0 + C e-ih0, отсюда AE = B + C. б)используя граничное условие [H(2)]my | x=t = [H(3)]my | x=t,получаем D e-p(t-t) = Beiht + Ce-iht ,отсюда D = Beiht + Ce-iht .
D = Beiht + Ce-iht ; x = t
Кроме того, учитывая, что в соответствии с (6) : dHmy/dx=-iweaEmz найдем с помощью (10) составляющую Emz и удовлетворим граничным условиям (9).
1/iwea1Aeqeqx при x < 0 ; Emz=1/iweadHmy/dx= 1/iwea2Beihx(ih)+ 1/iweaCe-ihx(-ih) при 0 £ x £ t;
1/iwea3De-p(x-t)(-p) при x > t; где ea1 = e1e0 , ea2 = e2e0 , ea3 = e3e0
а)используя граничное условие [E(1)]mz | x=0 = [E(2)]mz | x=0 , получаем qAEeq0/iwea1= ( ihB eih0– ihC e-ih0 )/ iwea2 , отсюда: qAE/ea1 = ( ihB – ihC )/ ea2. б)используя граничное условие [E(2)]mz | x=t = [E(3)]mz | x=t ,получаем -pD e-p(t-t)/ iwea3= ( ihBeiht – ihCe-iht )/ iwea2 , отсюда:-pD/ iwea3 = ( ihBeiht – ihCe-iht )/ iwea2 .
В результате получим дополнительную систему уравнений:
12. qAE/ea1 = ( ihB – ihC )/ ea2 x = 0 -pD/ iwea3 = ( ihBeiht – ihCe-iht )/ iwea2 ; x = t Четыре линейных однородных уравнения связывают четыре неизвестные постоянные AE, B, C, D, они линейно зависимы. Исключая из (11), (12)амплитудные коэффициенты AE, B, C, D, можно получить уравнение, связывающее числа h, q, p, то есть приравнять нулю определитель уравнений (11), (12), так как они имеют решение только в этом случае.

Раскроем соотношения (13), называемое характеристическим уравнением E-мод:
Поделим обе части уравнения на (еiht + e-iht) ¹ 0, и тогда получим:
Множитель Но нам все-таки необходимо использовать тангенс, как тригонометрическую функцию. Чтобы осуществить данный переход мы воспользуемся известной формулой: th( iht ) = -itg( -ht ). Применим данную формулу и поделим обе части уравнения на i, тогда получим:
Теперь выразим из вышеуказанного уравнения tght:
Теперь выполним ряд преобразований.


Домножаем числитель и знаменатель дроби на eа3eа1 ,и получаем:
Теперь сравним полученное уравнение с формулой тангенса суммы двух углов:
и получаем что : tga= qea2/hea1 , tgb=pea2/hea3 . Далее найдёмa, b: a=arctg(qea2/hea1)+kp=arctg(qe0e2/he0e1)+kp=arctg(q/h*(n2/n1)2) ,где e2=1/n22 , e1=1/n12а k –целое число 1,2,3,4…
b=arctg(pea2/hea3)+mp=arctg(pe0e2/he0e3)+mp=arctg(p/h*(n2/n3)2) ,где e2=1/n22 , e1=1/n12а m –целое число 1,2,3,4…
Теперь окончательно раскроем уравнение тангенса: tght=tg[(arctg(q/h*(n2/n1)2)+kp)+ (arctg(p/h*(n2/n3)2)+mp)], где k, m=0,1,2,3… Отсюда получаем: ht= arctg(q/h*(n2/n1)2)+kp+ arctg(p/h*(n2/n3)2)+mp, где k, m=0,1,2,3… Теперь объединим слагаемые kpи mpи получаем уравнение 14.
14. ht= arctg(q/h*(n2/n1)2)+ arctg(p/h*(n2/n3)2)+lp, где l=m+k=0,1,2,3...-индекс моды.
Уравнение (14) называется характеристическим уравнением E-мод, в котором l-это индекс моды. Из (14) видно, что при данной толщине диэлектрического волновода t существует множество решений (типов волн – мод) характеристического уравнения (14) с различными значениями поперечных волновых чисел h, q, p. Эти моды различаются индексом m и обозначаются как E 0, при m=0, E1, при m=1…и т.д. Учитывая дополнительные соотношения, следующие из (8а), (8б), (8в):
-h2 + k02e2=G2; 15. q2 + k02e1=G2; p2 + k02e3=G2; Исключая в них постоянную распространения G, можно получить ещё 2 уравнения, которые связывают h, q, p.
p2 + k02e3= -h2 + k02e2 p2 + h2 = k02 ( e2 – e3 ) Обозначив через nn=Öenкоэффициент преломления среды (n=1,2,3..), получим полную систему уравнений, определяющих E-моды.
q2 + h2 = k02 ( n22 - n12 ) ; 16. p2 + h2 = k02 ( n22 – n32 ) ; ht = arctg(q/h*(n2/n1)2)+ arctg(p/h*(n2/n3)2)+lp;
Используя (11), (12)и (6), выразим комплексные амплитуды составляющих поля E-мод через произвольную амплитудную постоянную AE и поперечные волновые числа h, qи p:
B = AE – C B = (AEq/ea1+ihC/ea2)/(ih/ea2)
Исключим Bи получим:
Теперь, зная С найдём В: B = AE – C= AE (1-1/2-iqea2/ 2hea1)= AE (1/2-iqea2/ 2hea1) б)Так как из (11) следует, что D=Beiht+Ce-iht,то найдем D: D= AE (1/2-iqea2/ 2hea1) eiht+ AE (1/2+iqea2/ 2hea1)e-iht
в)По известной формуле Эйлера:eiz = cosz + isinzзаменим eiht на (cosht+isinht)а также e-iht на (cosht-isinht)и в выражении полученном в пунктеб) тогда получим: D=AE (1/2-iqea2/ 2hea1)(cosht+isinht)+AE (1/2+iqea2/ 2hea1)(cosht-isinht)= = AE 1/2cosht+ AE 1/2cosht+qea2/ 2hea1 sinht+qea2/ 2hea1 sinht= = AEcosht+ AE qea2/ hea1sinht,так как ea2/ea1=e0e2/e0e1=n22/n12,то D=AEcosht+AEq/h(n2/n1)2sinht=AEq/h(n2/n1)2(sinht+h/q(n2/n1)2cosht) Теперь соберем все вместе, подставляя найденные значения B, C, D в (10), получим:
AE eqx при x < 0; Hmy= AE (q/h)(n2/n1)2[sin hx + (h/q)(n2/n1)2cos hx] при 0 £ x £ t; AE (q/h)(n2/n1)2 [sin ht + (h/q)(n2/n1)2 cos ht] e-p(x-t)при x > t; Таким образом, мы нашли составляющую Hmy,поле для Е-мод.
Emz=1/iwea(dHmy/dx)=1/iwe0en(dHmy/dx)=1/iwnn2e0(dHmy/dx) Emx=G/wea(Hmy)=G Hmy/we0en=GHmy/wnn2e0,, где n=1,2,3…
Таким образом, мы выполнили поставленную задачу – определили составляющие Hmy, Emx , Emz волн Е – типа в планарном диэлектрическом волноводе. Следует также отметить, что комплексную постоянную АЕ мы не определяем, поскольку исследуем «свободные», то есть не зависящие от источника возбуждения волн. Модуль и фаза постоянной AEзависят от амплитуды и фазы источника возбуждения.
РЕШЕНИЕ ЗАДАЧ Задача №15 Определить толщину симметричного ДВ из полистирола (ε = 2,56), при которой вдоль Дв распространяется только основная волна электрического типа Ео. Длина волны генератора λо = 4,5 см, ε1= ε3=1,5.
Дано: ε1= ε3=1,5 ε2=2,56 λо = 4,5 см = 0,045 м
Найти: t=2d, при которой существует Ео
Решение В задаче требуется найти толщину диэлектрической пластины (2d), в которой будет распространяться только электрическая волна, имеющая нулевую моду (m=0). Известно, что число мод (m) распространяющихся в симметричном ДВ зависит от параметров λо, n1, n2 и d. Эта связь выражается формулой:
m
Данное условие имеет следующий физический смысл: волна в диэлектрическом волноводе может распространяться только при частоте выше критической, т.е. при частоте ниже критической (Г< kоn1) в диэлектрическом волноводе моды данного типа вообще нет. С точки зрения математики, при неправильно подобранных параметрах λо, n1, n2,d и m характеристическое уравнение может не иметь решения (волновые числа h, p, q могут быть отрицательными). n12 = ε1 = 1,5 n22 = ε2 = 2,56 m = 0
0 ≤ 2d · 0 ≤ 2d ·
Полученная величина t = 2,587 ≈ Ответ: приt < 2,587 см в ДВ будет распространяться волна Ео типа.
Задача №16
Определить фазовую скорость волны Ео, распространяющуюся в ассиметричном ДВ, толщиной t = 10 мм, ε1 = 1,0, ε2 = 2,9, ε3 = 2,8. Длина волны генератора 10 мм. Построить график распределения компоненты Ну в направлении, перпендикулярном диэлектрической пластине. Дано: ε1=1,0 ε2=2,9 ε3=2,8 λ0=10·10-3 m0=0 Найти: Решение Проверка условия на существование данной волны: n1 = n2 = n3 =
Решение системы (характеристического уравнения): h = 1; p = 1; q = 1 TOL = 10-9 Given
Ответ: h = 186,245289 P = 69,217843 d = 845,814771 Проверка:
Г = 1053,6540242 – постоянная распространения с = 3·108
Ответ: υф = 1,7889701∙108 Построение графика распределения компоненты Ну: АЕ = 1 Hmy(x) =
Hmy(0) = 1
Поиск максимального поля волны:
Максимальное значение поля: Определим, какая доля энергии приходится на внутренний слой: η·100 = 38,000313 % В процентном соотношении приходится 38 % волны на внутренний слой
Источники и литература: 1. Андрушко Л.М., Гроднев И.Н., Панфилов И.П. Волоконные оптические линии связи. М., 1985. – 136 с. 2. Взятышев В.Ф. Диэлектрические волноводы. М., 1970. – 118 с. 3. Вольман В.И., Пименов Ю.В. Техническая электродинамика. М., 1971. – 487 с. 4. Гринев А.Ю., Котов Ю.В. Поверхностные электромагнитные волны в планарных диэлектрических волноводах. М., 1989. – 48 с. 5. Никольский В.В. Электродинамика и распространение радиоволн. М., 1978. – 607 с. 6. Сборник задач по курсу «Электродинамика и распространение радиоволн»/Под ред. С.И. Баскакова. М., 1978. – 607 с. 7. Унгер Х.Г. Планарные и волоконные оптические волноводы/Под ред. В.В. Шевченко. М.,1980. – 656 с. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 274. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 “ “ “ “ “ “ “ “ “ “ “ “ “ “
“ “ “ “ “ “ “ “ “ “ “ “ “ “ 




 ~ ~ ~ ~ ~ ~ ~ ~ ~
~ ~ ~ ~ ~ ~ ~ ~ ~






 Для E-мод -iGEmx - dEmz/dx=-iwmaHmy
Для E-мод -iGEmx - dEmz/dx=-iwmaHmy


 11. AE = B + C x = 0
11. AE = B + C x = 0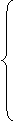
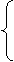







 является гиперболическим тангенсом[ th(iht) ].
является гиперболическим тангенсом[ th(iht) ].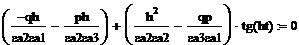


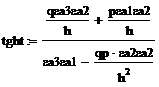






 q2 + k02e1= -h2 + k02e2 q2 + h2=k02 ( e2- e1 )
q2 + k02e1= -h2 + k02e2 q2 + h2=k02 ( e2- e1 ) 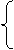 a)Сначала из (11) выразим постоянную B:
a)Сначала из (11) выразим постоянную B: 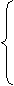
 ≤ 2d
≤ 2d  ≤ (m + 1)
≤ (m + 1) 
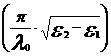 ≤
≤ 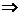 0 ≤ 2d ≤
0 ≤ 2d ≤ 

 см
см ф для волны Е0-типа
ф для волны Е0-типа =1,570796 <
=1,570796 <  = 1,986918
= 1,986918 n1 = 1
n1 = 1 n2 = 1, 702939
n2 = 1, 702939 n3 = 1, 67332
n3 = 1, 67332 k = 628,318531
k = 628,318531 


 h ≥ 0; p ≥ 0; q ≥ 0
h ≥ 0; p ≥ 0; q ≥ 0

 Г = 1053,6540242
Г = 1053,6540242 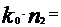 1069,987902
1069,987902  Г = 1053,6540242
Г = 1053,6540242 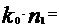 628,318531
628,318531 
 Г = 1053,6540242
Г = 1053,6540242  1051,377997
1051,377997  - скорость света в вакууме
- скорость света в вакууме  1,761661∙108
1,761661∙108  ω = 1,884956·1011 с-1 υф = 1,7889701∙108
ω = 1,884956·1011 с-1 υф = 1,7889701∙108 
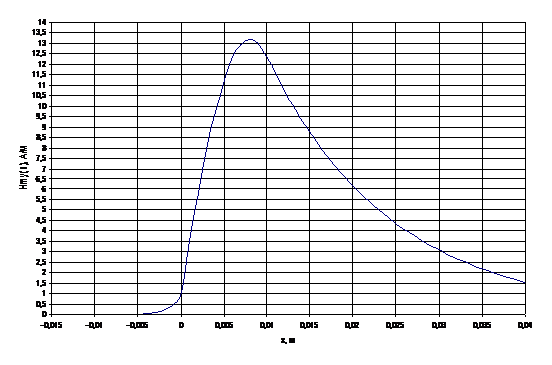
 Hmy(t) = 12,32634
Hmy(t) = 12,32634  = 11,163887
= 11,163887 

 м
м 


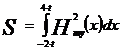
 S = 0,253127 η =
S = 0,253127 η = 