Четко и нечетко поставленные задачи

Ну вот, перед вами Винни-Пух. Как видите, он спускается по лестнице вслед за своим другом Кристофером Робином, головой вниз, пересчитывая ступеньки собственным затылком: бум-бум-бум. Другого способа сходить с лестницы он пока не знает. Иногда ему, правда, кажется, что можно бы найти какой-то другой способ, если бы он только мог на минутку перестать бумкать и как следует сосредоточиться (А. А. Милн. Винни-Пух и все-все-все... Пер. Б. Заходера).

Задачи бывают различных типов и уровней сложности. Рассмотрим следующие две задачи.

1. Задача определения площади параллелограмма (Wertheimer, 1959). Когда-то, в пятом или шестом классе, вы учили, что площадь прямоугольника определяется умножением его длины на высоту. Пусть теперь вам дан параллелограмм длиной 4 см и высотой 2 см. Какова его площадь?

2. Сочините поэму, описывающую чувства, которые вы испытываете при появлении первых распустившихся весенних цветов.

Эти задачи кажутся вам качественно совершенно разными, не правда ли? Задача параллелограмма имеет единственное точное решение. Вы его нашли? Вертхаймер (Wertheimer, 1959) указал, что правильное решение заключается в реорганизации восприятия, или представлении задачи в новой форме. В данном случае следует (400:) мысленно представить параллелограмм в виде прямоугольника и двух треугольников. Параллелограмм приобретает следующий вид:

После того как задача преобразована таким образом, остается сделать небольшое усилие и сообразить, что площадь параллелограмма может быть определена по той же формуле, что и площадь прямоугольника, поскольку, сдвинув один из треугольников к другому, мы получим прямоугольник длиной 4 см и высотой 2 см. В приведенном примере площадь параллелограмма равна 2 см х 4 см = 8 см². Другого правильного ответа просто не существует. Цель (правильный ответ) в данном случае является четко поставленной, так же как и путь достижения этой цели.

Написание поэмы — это задача совсем иного рода. Цель (создание поэмы, выражающей восхищение) поставлена нечетко, здесь могут быть выбраны различные пути ее достижения. Существует бесчисленное множество способов написания поэмы. Самая большая сложность в данном случае состоит в оценке качества конечного продукта. Цель в нечетко обозначенной задаче сама является неопределенной, поэтому некоторая сложность заключается также в том, чтобы вообще понять, решена или нет задача (Dorner, 1983).

Большинство задач, с которыми люди сталкиваются за пределами школы, поставлены нечетко. Человек, занятый решением задачи, должен сам обозначить цель и затем оценить, насколько полно она достигнута. И наоборот, большинство задач, которые ставятся перед студентами в учебном заведении, четко поставлены; это означает, что они имеют единственный правильный ответ. Другими примерами нечетко поставленных задач служат: внедрение способа увеличения количества торговых сделок в бизнесе, открытие новых, более эффективных форм обучения, создание написанного доступным языком учебника, накопление денег для платы за обучение, усовершенствование мышеловки, ограничение производства ядерного оружия, назначение свидания привлекательной однокласснице, оздоровление окружающей среды и т.д. В нечетко поставленных задачах цель может быть расплывчатой или не подразумевающей завершенности, что создает сложности при выработке путей решения задачи и еще больше усложняет их оценку.

Одним из наилучших путей решить нечетко поставленную задачу является постановка четкой цели. Обычно в таких случаях цель можно установить несколькими способами. Например, задача повышения числа торговых сделок может быть переопределена в задачу повышения прибыли, поскольку реальная цель заключается именно в нахождении путей получения большей суммы денег. Представленная в такой форме задача меняет свою первоначальную формулировку. Пути решения теперь могут включать в себя сведение к минимуму убытков, уменьшение товарно-материальных запасов, получение невыплаченных долгов. Наилучший способ решения нечетко поставленных задач — это обозначить несколько целей, которые в результате приведут к желаемому результату. Когда бы вы ни сталкивались с такой задачей, старайтесь наметить себе по меньшей мере четыре пути достижения цели. Такой подход предоставит вам дополнительные варианты и сможет облегчить поиски наилучшего способа решения. (401:)

Иногда трудно определить, четко или нечетко поставлена задача. Вспомним задачу с поездкой в аэропорт. Если считать, что она заключается в выборе одной из трех дорог, ведущих в аэропорт, то она четко поставлена, но если возможны другие пути решения и цели — например, полет в аэропорт, использование другого самолета из ближайшего аэропорта, пользование подземкой, — то формулировка задачи становится более расплывчатой. Даже если задача на первый взгляд кажется четко поставленной, полезно рассмотреть, нельзя ли прийти к ее решению, установив иные цели — а если так, то какие пути решения задачи возможны для достижения этих целей.

Планирование и представление задачи

Во время уроков по математике и прочим предметам, которым я обучался в колледже, меня чрезвычайно раздражала потеря того огромного количества времени, когда я, уставившись на задачу, не имел ни малейшего представления, какой шаг следует сделать дальше, чтобы приблизить решение. Тогда я думал, что эти потерянные минуты не имеют никакого воспитательного значения — не вижу в них смысла и сегодня

Викелгрен (Wickelgren, 1974, р. IX)

Последние исследования в области решения задач сфокусированы на важности построении плана для поиска и отбора решений (Friedman, Scholnick, & Cocking, 1987). Планирование является одним из самых главных навыков мышления, который используется для управления поведением и его регуляции (Pea & Hawkins, 1987; Scholnick & Friedman). План дает конкретную схему, следуя которой шаг за шагом человек приближается к достижению желаемой цели. При этом следует обдумать по меньшей мере четыре способа достижения конечной цели, даже если задача кажется четко поставленной. Такой подход увеличит размеры пространства задачи и обеспечит более благоприятные возможности для поиска оптимального решения. Такой вид плана называется трансконтекстуальным, что по сути означает, что он может быть использован в любом контексте при решении задач разного рода (Ceci & Ruiz, 1993). Для иллюстрации этого подхода приведем наглядный пример.

Многочисленные опросы общественного мнения показали, что борьба с «криминальной угрозой» является задачей номер один для большинства американцев. Поэтому неудивительно, что политики сделали ее основным пунктом своих предвыборных обещаний. Борьба с «криминальной угрозой» — это важная и в то же время нечетко поставленная задача. Попробуем сформулировать ее таким образом, чтобы цель была четко выраженной.

Цель № 1. Снизить преступность. Каковы возможные решения этой задачи? Как вывести общество из его нынешнего состояния страха перед «криминальной угрозой»? Как снизить уровень преступности? Ниже приведены два возможных пути достижения этой цели.

• Принять закон о разрешении применения смертной казни.

• Давать преступникам пожизненный срок заключения, если они признаются виновными в третьем по счету серьезном преступлении. (402:)

Теперь давайте сформулируем эту цель по крайней мере четырьмя различными способами и рассмотрим, к какому решению приведет каждая из формулировок. Посмотрим на задачу с различных точек зрения. Итак, достижение каких целей может послужить на благо горожанам, Которые являются потенциальными жертвами преступности?

Цель № 2. Сделать безопасной жизнь честных граждан. При постановке такой цели внимание фокусируется уже не на преступниках, а на их потенциальных жертвах. Вот некоторые возможные варианты достижения этой цели, которые сразу же приходят в голову.

• Обеспечить лучшую охрану честных граждан.

• Обучить каждого приемам самозащиты.

• Организовать в каждом микрорайоне народную дружину.

Цель № 3. Снизить число преступников. Эта цель фокусирует внимание скорее не на методах борьбы с преступностью, а на количественных показателях правонарушений Примеры решений.

• Ссылать преступников в Сибирь.

• Вернуться к средневековым методам наказания — виселице и публичной порке, чтобы предотвратить потенциальные преступления.

• Проводить широкомасштабные мероприятия, направленные на сдерживание преступности (например, повышение уровня образования, внедрение спортивных программ и т. д.).

Цель № 4. Изменить отношение людей к преступности — добиться того, чтобы они не боялись преступников. При такой формулировке поставленная цель будет содействовать не столько снижению уровня преступности, сколько изменению общественного мнения. Вот несколько возможных путей достижения этой цели.

• Дать каждому человеку, испытывающему страх перед преступностью, успокоительные средства, чтобы снизить беспокойство (они больше не будут испытывать страха).

• Распространять информацию о том, что фактический уровень преступности крайне низок (это может быть либо правдой, либо ложью; в любом случае такое действие служит достижению этой цели — хотя ложь, естественно, является неэтичным приемом).

Цель № 5. Снизить число тяжелых преступлений. Эта цель также меняет наше восприятие преступности, так как касается снижения степени тяжести, а не количества преступлений, числа преступников и страха людей перед преступностью. Некоторые возможные решения.

• Запретить ношение оружия.

• Легализовать употребление наркотиков.

Можно по-новому сформулировать цель, посмотрев на задачу с позиции преступников. Что могло бы воспрепятствовать совершению ими преступлений? Вскоре станет ясно, что преступники не являются однородной массой, и нужны разные действия против различных типов преступлений Предположим, что вы угонщик машин. Что могло бы остановить вас? Быть может, наличие работы? А может, вас пристыдит жена? Что может остановить преступления такого типа? (403:)

Безусловно, некоторые из приведенных вариантов решения задачи смешны и нелепы — такие, например, как ссылка преступников в Сибирь или выдача каждому человеку успокоительных средств, другие — просто неэтичны. Идея этого примера заключалась в том, чтобы показать, как с помощью различного представления цели нечетко поставленной задачи выявляются новые точки зрения на нее. Вполне вероятно, что в данном случае необходимо принять комбинированное решение, и тогда главный страх Америки уменьшится. Попробуйте проделать такую операцию с другими сложными задачами. Не исключено, что, взглянув на задачу с разных точек зрения, вы будете удивлены, обнаружив множество неожиданных вариантов решений, возникающих при рассмотрении различных формулировок конечной цели.

Большинство программ, посвященных усовершенствованию навыков решения задач, делают основной упор на «планомерном подходе» (Covington, 1987). В настоящее время доступны многочисленные компьютерные программы, предлагающие планы решения задач. Компьютерный бум способствовал появлению большого количества новых программ, которые претендуют на повышение у пользователей на-

Рис. 9.2. Совет детям, как разработать план решения задачи (Источник Covington, Crutchfield, Davies & Olton, 1974, p 17 )

404

выков решения задач, однако большинство из этих программ настолько ново, что еще не накоплено достаточного объема данных, подтверждающих их эффективность.

Несмотря на то что планы решения задач могут отличаться друг от друга своей сложностью, большинство из них складывается из пяти основных шагов: а) осознание того, что задача действительно существует (Это важная стадия, которая часто служит признаком творчества — понятия, которому посвящена глава 10. Рассмотрим любые перемены — например, переход от использования извозчиков к моторизованным видам транспорта. В большинстве стран лошади работали без нареканий, и предложение заменить их сомнительным ящиком на колесах, который часто ломается и нуждается в постоянных заправках горючим, казалось в то время просто нелепым. Большинство людей без всяких проблем путешествовало на лошадях); б) -формулировка задачи, в которую включается определение исходного положения и окончательной цели; в) выработка и оценка возможных решений; г) выбор оптимального решения; д) реализация выбранного пути решения задачи с целью его проверки.

К сожалению, если цель не будет достигнута, все или почти все шаги придется повторить. Не исключено, что потребуется изменить формулировку цели, разработать дополнительные варианты решения и последовательно оценить каждый из них.

Брэнсфорд и Штейн (Bransford & Stein, 1993) использовали слово-акроним ИДЕАЛ (IDEAL), чтобы обозначить эти пять стадий: / (Identify — идентификация или осознание задачи); D (Define — определение и представление задачи); Е (Explore — разработка возможных решений); A (Act — действие согласно выработанной стратегии); L (Look back — взгляд назад и оценка последствий действий).

Главной целью Программы продуктивного мышления (Covington, Crutchfield, Davies & Olton, 1974) — одной из самых старых и наиболее популярных программ, целью которой было помочь ребенку «научиться думать», — являлось приобретение привычки планировать стратегию выработки решения. На рис. 9.2 показано несколько фрагментов из этой программы, в которой делался упор на необходимости соблюдения строгого порядка при решении задач.

Наилучший путь решения задачи — придумать наиболее удачное ее представление. Это заставляет человека, занятого поиском решения, четко определять желаемую цель и тщательно планировать каждый шаг достижения этой цели. Майер (Mayer, 1992) обнаружил, что наглядное визуальное представление помогает читателям при понимании сложного текста. Одним из принципов правильного мышления, который упоминается почти во всех главах, является использование системы разнообразного представления имеющейся информации — в виде диаграмм с текстовыми пояснениями или словесных описаний с рисунками.

Представление задачи хорошо демонстрирует степень ее понимания (Greeno, 1973,1992). Удачное представление имеющейся информации должно содержать всю имеющуюся релевантную информацию и выявлять связи между отдельными составляющими (правила и ограничения) — это значительно облегчит продвижение к цели. Правильное представление задачи — определяющий момент в процессе нахождения решения.

Рассматривая способы удачных представлений задачи, Ньюэл (Newell, 1983) отметил, что «необходимо пощекотать память» — эту фразу я очень часто употребляю, поскольку считаю_гчто она отражает ключевой момент при рассмотрении про-

405

цесса мышления. Это означает, что нужно задействовать все знания человека о решаемой задаче. Когда человек правильно сформулирует задачу и правильно ее представит, он, легко уловив имеющиеся связи, сразу же поймет, какая информация пропущена, а какая является противоречивой.

Попробуем показать это на примере:

Представьте в графическом виде и в виде алгебраической формулы высказывание «В этом университете студентов в шесть раз больше, чем профессоров»

Если вы похожи на большинство студентов колледжа, вы нарисуете подобную диаграмму:

Это соответствует формуле 6S = Р.

Если бы я назвала вам число студентов, то вы могли бы, используя эту формулу, определить количество профессоров, и наоборот. А вы заметили, что формула, выведенная из такого графического представления, содержит ошибку? Формула показывает, что профессоров больше, чем студентов — т. е. все наоборот! Причина, по которой многие студенты испытывают сложности при решении этой и подобных задач, лежит в неправильной интерпретации слов. Сочетание слов «студентов в шесть раз больше» сразу вызывает желание умножить число студентов на шесть. Майер нашел метод, как существенно повысить эффективность решения математических задач студентами колледжа всего лишь после трехчасового занятия, на котором их учили правильно графически представлять задачи (Lewis & Mayer, 1987). Трудно переоценить значение правильного представления задачи при ее решении.

Следующие пункты содержат руководства по правильному представлению задач и демонстрируют тесную связь между представлением задачи и ее решением. Правильное представление сразу же выявляет характерные особенности задачи. Оно классифицирует информацию, размещая ее в пространстве и делая наглядной; кроме того, оно служит проверкой, насколько хорошо мы понимаем задачу.

Запишите задачу

Все задачи изначально представлены в вашей голове. Хорошо было бы выписать на бумагу пути решения задачи и ее цели или отобразить их в другой конкретной форме. Это снизит нагрузку на память и позволит вам ознакомиться с наглядным представлением задачи. Простейший пример помощи, которую могут оказать карандаш и бумага, это решение элементарной задачи на умножение. Попробуйте решить задачу, ничего не записывая:

976 х 893 (406:)

Естественно, вы задумаетесь над этим пустяковым вопросом, поскольку он является простым, когда у вас под рукой карандаш и бумага, и сложным, требующим хорошей памяти, для вычисления в уме. Всегда, когда нужно сохранить в памяти ряд фактов или вариантов, полезно воспользоваться карандашом и бумагой.

Нарисуйте график или диаграмму

«Медведь, выйдя из точки Р, прошел одну милю на юг. Затем он изменил направление и прошел милю на восток. Потом он снова повернул налево и прошел одну милю на север, после чего оказался точно в том месте, откуда стартовал. Какого цвета был медведь?» (Polya, 1957, р. 234).

Задача кажется вам странной или даже неразрешимой? Если вы нарисуете простую «карту» путешествия медведя, она будет похожа на клиновидный кусок пирога. В каком месте земного шара это возможно? Вспомните о глобусе. Наверное, вы сразу воскликните: «Ну конечно же, точка Р— это Северный полюс» Как только вы разобрались, что находитесь на Северном полюсе, задача сразу становится легкой. Медведь должен быть белым, поскольку на Северном полюсе живут только белые медведи.

Давайте рассмотрим еще одну задачу. Старый почтенный монах покидает свой монастырь ровно в 6 часов утра, чтобы взобраться по извилистой горной тропе на вершину и там уединиться. Он достигает вершины ровно в 4 часа вечера. Проведя на вершине ночь во сне и молитвах, он покидает вершину горы ровно в 6 часов утра и добирается до монастыря ровно в 4 часа вечера. Никаких ограничений на скорость монаха не накладывается. Известно, что по пути он несколько раз останавливается, чтобы отдохнуть. Спрашивается, существует ли на горной тропе такая точка, которую монах проходит в одно и то же время суток?

Остановитесь и подумайте некоторое время над этой задачей. Она вам кажется сложной? Есть два подхода, которые сделают ответ простым и очевидным, но прежде чем вы продолжите чтение, решите, какие шаги предприняли бы вы для отыскания решения, и попробуйте найти его. Как вы уже вероятно догадались, правильное представление задачи обеспечит успех в ее решении.

Одно из решений состоит в построении графиков подъема и спуска монаха. Графики могут иметь произвольную форму, поскольку мы ничего не знаем о характере движения монаха. Примеры графиков подъема и спуска приведены на рис. 9.3.

Теперь наложите эти графики друг на друга и посмотрите, пересекаются ли они в какой-нибудь точке. Если такая точка существует, то это означает, что в каждый из двух дней монах побывал в ней в одно и то же время. Это показано на рис. 9.4. Построение графика сделало решение наглядным. В действительности существует еще более простое решение этой задачи, если изменить ее формулировку и представить условие в эквивалентной, но несколько другой форме. Предположим, двое людей идут по одной и той же горной тропе в одно и то же время и в одно и то же утро. Если один из них вышел из монастыря, а другой с вершины горы, оба начали движение в 6 часов утра и пришли в конечный пункт своего маршрута в 4 часа вечера, то очевидно, что где-то на тропе они должны были обязательно встретиться, независимо от того, как часто каждый из них останавливался передохнуть или поду-

Рис. 9.3. Графики подъема и спуска монаха.

Графики имеют произвольную форму, поскольку монах мог отдыхать, когда хотел, — как при подъеме на вершину, так и при спуске с нее.

Рис. 9.4. Накладывая друг на друга графики подъема и спуска, легко можно увидеть, что обязательно должно быть место, где они пересекаются. Таким образом, должно существовать место на горной тропе, которое монах пересекал в каждый из дней в одно и то же время.

408

мать. Таким образом, при изменении формулировки сложная задача может превратиться в тривиальную.

Графическое изображение нередко является отличной стратегией решения задач. Несколько лет назад я проводила лабораторный курс экспериментальной психологии. Заключался он в следующем: студентам требовалось выполнить эксперименты, собрать данные и, переосмыслив их, предложить свою интерпретацию. И хотя студенты изучали статистические методы, необходимые для такой работы, я заметила, что они добивались гораздо большего понимания исследуемой задачи, если представляли полученные ими результаты в виде графиков. Это помогало им формулировать выводы на базе экспериментальных данных, поскольку они лучше понимали природу этих данных. Студенты обнаружили, что простейший график оказался значительно более эффективным средством для понимания задачи, чем разработанные статистические процедуры, к которым они должны были прибегнуть.

Особенно полезны графики и различные виды диаграмм для понимания стратегии решения математических и других точных задач. Например, есть известная задача из начального курса статистики, когда требуется отыскать площадь фигуры, ограниченной отрезком «колоколообразной» кривой нормального распределения между двумя заданными точками. Для студентов это может показаться сложной и непонятной задачей, но если они начертят кривую и заштрихуют область, площадь которой надо отыскать, задача значительно упростится. Я не даю своим студентам математических формул для отыскания необходимых площадей. Студентам проще вывести их самим, ориентируясь на построенные графики и рисунки.

Давайте рассмотрим геометрическую задачу, предложенную Кёлером (Kohler, 1969). В вашем распоряжении есть только данные, приведенные на рис. 9.5, и известно, что радиус окружности равен 5 см. Сможете ли вы определить длину отрезка L?

Одна из причин сложности этой задачи — ее данное графическое представление, когда отрезок L оказывается гипотенузой двух прямоугольных треугольников:

Рис. 9.5. Пользуясь лишь той информацией, которая приведена на рисунке, попробуйте определить длину отрезка L. (Источник: Kohler, 1969)

409

Рис. 9.6. В качестве дополнительного построения для нахождения решения задачи (рис. 9.5) проведены радиусы. Можете ли вы теперь определить длину отрезка L?

треугольника со сторонами X, Д L и треугольника, образованного пересечением с линией L двух взаимно перпендикулярных радиусов. Как изменить этот рисунок, чтобы решение стало наглядным?

Проанализируйте данную информацию. Поскольку единственным заданным на рисунке линейным размером является радиус окружности, то, вероятно, он потребуется для решения задачи. Попробуйте начертить дополнительные радиусы внутри окружности, как это показано на рис. 9.6. Может, это поможет вам предложить вариант решения?

Посмотрите внимательно на квадрант, содержащий отрезок L. Можете ли вы найти другой отрезок, равный по длине L? Если вы представите отрезок L как диагональ прямоугольника со сторонами X, D и необозначенными сторонами, являющимися отрезками горизонтального и вертикального радиусов, то другая диагональ этого прямоугольника должна равняться по длине L. В то же время другая диагональ является не чем иным, как радиусом; таким образом, длина отрезка L равна радиусу и тоже составляет 5 см. Хотя первоначальное представление задачи вводило в заблуждение, с помощью дополнительных построений решение найдено.

Конечно, сразу не было ясно, что построение дополнительных радиусов окружности приведет к решению задачи. Но тем не менее было очевидно, что ответ в любом случае будет зависеть от радиуса, поскольку он является единственным данным размером, а цель заключалась в нахождении длины отрезка L. Те действия, которые вы предприняли, чтобы трансформировать данные задачи по ходу ее решения, повлекли за собой уяснение сути задачи. Но если бы вы не знали, что диагонали прямоугольника равны, вы не смогли бы решить задачу. Люди, успешно решающие задачи, накапливают солидный багаж знаний, который пополняется на протяжении всего периода обучения — причем это происходит как в учебном заведении, так и за его пределами. Залог успешного решения задач — это обширные знания во многих областях жизни.

Попробуем решить другую задачу, в которой поиск пути решения задачи также должен сопровождаться графическим представлением. (410:)

Мелвин, Брок, Марк и Клэр, чтобы сэкономить деньги и сохранить душевное спокойствие, решили организовать кооператив по присмотру за детьми. Они договорились сидеть с детьми друг друга на следующих условиях: если один из них остается с чьими-то детьми, то последний должен «заплатить» за это таким же количеством часов присмотра за чужими детьми. Подсчитывать баланс времени, которое каждый из них проработал «приходящей нянькой», они решили в конце месяца. Оказалось, что в течение месяца Мелвин сидел с детьми Брока 9 часов, Марк сидел с детьми Мелвина 3 часа, а Клэр оставалась с детьми Мелвина 6 часов. Марк 9 часов нянчился с детьми Клэр, и Брок 5 часов следил за ее детьми. Кто кому должен 12 часов отработки?

Очевидно, что хорошая схема, отражающая связи между этими людьми, просто необходима. Соответствующие данные помогут связать этих четверых с количеством часов, которые они должны друг другу. Начнем с первого предложения: «Мелвин сидел с детьми Брока 9 часов». Таким образом, Брок должен Мелвину в конце месяца 9 часов. При этом используется операция перевода количества часов, затраченных на присмотр за ребенком, в количество часов, «полученных» каждой «нянькой». Простейшая схема этого процесса имеет вид:

Следующая фраза трансформируется так: «Мелвин должен 3 часа Марку и 6 часов Клэр».

Затем, преобразовав третью фразу, мы получим: «Клэр должна Марку 9 часов и Броку5 часов».

 (411:)

Рис. 9.7. Альтернативная форма представления задачи кооператива по уходу за детьми

Легко видеть из построенной схемы, что только Марку должны быть возвращены 12 часов присмотра за детьми — 3 часа от Мелвина и 9 часов от Клэр. Эта схема является необходимой частью решения поставленной задачи.

Существует несколько других способов представления информации в задаче о кооперативе по присмотру за детьми, которые отражают все существующие связи и таким образом позволяют получить правильный ответ. Когда моя коллега (д-р Сюзанна Намедэл из Калифорнийского государственного университета, Лонг-Бич) поставила эту задачу перед своими студентами, она обнаружила, что они в ходе поиска решения изобрели самые разные формы ее наглядного представления. Один из студентов использовал простейшую диаграмму, изображающую количество часов, затраченных каждым из участников. Представление условий задачи в такой форме приведено на рис. 9.7.

Некоторые студенты воспользовались различного рода таблицами. Кое-кто из них выписывал количество «отработанных» часов со знаком плюс, а число «одолженных» часов — со знаком минус Другой студент разделил исходную информацию на категории «работа няней» и «вызов няни», затем заполнил таблицу информацией, просуммировал по колонкам общее количество часов, которое каждый из

Таблица 9.1. Использование таблицы для наглядного представления информации в задаче о кооперативе по присмотру за детьми

412

Таблица 9.2. Альтернативный вариант использования таблицы для наглядного представления информации в задаче о кооперативе по присмотру за детьми

членов кооператива «просидел нянькой», а по строкам таблицы просуммировал общее количество часов, в течение которых каждый из них вынужден был прибегать к услугам приходящей няни. Эти формы представления условия задачи приведены в табл. 9.1 и 9.2.

Задача о кооперативе по уходу за детьми продемонстрировала, что существует несколько способов представления исходной информации. Попробуйте сами предложить различные наглядные представления задач, которые встретятся вам в этой главе. Правильное представление задачи содержит всю существенную информацию, которая представлена так, что может быть легко понята и усвоена. Кроме того, правильное представление подсказывает путь к решению задачи.

Попытайтесь построить иерархическое дерево

Иерархические деревья — это тип разветвленных диаграмм. Наиболее часто они применяются, когда надо математически оценить вероятность случайных исходов. (См. главу 4 об использовании древовидных диаграмм в решении задач типа «если... то...» и главу 7 об использовании дерева решений в расчетах вероятностей.) Иерархические деревья или древовидные диаграммы могут оказаться полезными при решении задач и принятии решений. В таком контексте они называются деревом решений. (Как отмечалось ранее в этой главе, различие между решением задачи и принятием решения несколько искусственно, поскольку они тесно взаимосвязаны.)

Если задача, над которой вы работаете, слишком сложна и каждый возможный путь решения разветвляется на дополнительные пути, то следует обратиться к помощи иерархического дерева, или древовидной диаграммы.

Вот, например, классическая задача, впервые предложенная Дункером (Duncker, 1945). Хотя предлагаемая в ней проблема является медицинской, никаких специальных знаний для ее решения не потребуется.

У пациента неоперабельная опухоль в желудке. Задача состоит в том, чтобы придумать способ избавления от этой опухоли с помощью рентгеновских лучей, при котором не будут повреждены здоровые ткани, окружающие опухоль со всех сторон.

Остановитесь на несколько минут и подумайте, какой путь вы выбрали бы для решения этой задачи? (413:)

Большинство людей, занятых решением задачи Дункера (Duncker, 1945), продвигались к цели в несколько этапов. Хотя были опробованы различные решения, лучшим из них оказалось применение нескольких слабых лучей, каждый из которых проникал в тело снаружи со своей, отличной от других позиции — при этом все лучи фокусировались и собирались воедино в месте расположения опухоли. Таким образом, лучи слабой интенсивности не наносят вреда здоровым тканям, а опухоль при этом подвергается интенсивному лучевому воздействию. Такой подход пришел в голову после перебора различных способов решений, которые подразумевали резкий рост интенсивности лучей в районе расположения опухоли.

Одна из предпринятых попыток поиска путей решения задачи с помощью иерархического дерева проиллюстрирована на рис. 9.8. Заметьте, что цель обязательно располагается в вершине дерева. Общие стратегии перечисляются одним уровнем ниже цели, наиболее характерные пути, определяющие каждую стратегию, — еще одним уровнем ниже.

В частности, древовидные диаграммы оказываются весьма полезными, если исходная информация сама по себе имеет иерархическую структуру. Например, классификация всех живых организмов выстроена биологами в иерархическую схему. Если вы спросите ребенка, является ли пчела животным, он, вероятно ответит: «Нет, поскольку это насекомое». Этот вопрос можно ему разъяснить, если нарисовать биологическое классификационное дерево, пример которого приведен на рис. 9.9.

Другой пример использования древовидных диаграмм для решения задач — это применение хорошо известного генеалогического дерева. Занимающиеся вопросами недвижимости юристы, которые часто сталкиваются с запутанным клубком родственных связей, должны уметь определять степень родства всех членов семьи, чтобы контролировать выполнение условий завещаний и уплату налогов на имущество.

Рис. 9.8. Диаграмма в виде иерархического дерева, иллюстрирующая одну из попыток решения сформулированной Дункером задачи рентгеновского облучения (Duncker, 1945).

414

Рис.9.9. Диаграмма в виде иерархического дерева, которая поможет ответить на вопрос:

«Являются ли пчелы животными?»

Многочисленные отчимы и мачехи, сожители, пасынки, падчерицы, сводные братья и сестры, незаконнорожденные дети могут превратить сложный вопрос наследства в сущий правовой кошмар. Аккуратное построение генеалогического дерева, которое разместит каждого родственника на соответствующей ветке, является просто бесценным средством решения запутанных задач наследования.

Постройте матрицу

Матрица — это расположение фактов или чисел в прямоугольном порядке. На самом деле это просто более замысловатое слово для таблицы. Когда исходные данные в задаче могут быть разбиты на отдельные категории, матрица может оказаться удобным способом для их представления. Рассмотрим задачу, сформулированную Уимби и Лоххедом (Whimbey & Lochhead, 1982):

Трое молодых людей — Фред, Эд и Тед — женились на Джоан, Салли и Викки (не обязательно в таком порядке). Джоан, будучи сестрой Эда, живет в Детройте. Фред не любит животных. Эд весит больше, чем муж Викки. А у мужа Салли есть хобби: разводить сиамских котов. Фред тратит на регулярные поездки от своего дома в Энн-Эрбор до работы в Детройте свыше 200 часов в год. Определите, кто на ком женат (р. 67).

Каков тип исходных данных в этой задаче? Данные касаются мужей и жен. Постройте матрицу 3 х 3 и заполните ее, насколько возможно, в соответствии с полученной информацией:

Поскольку Джоан является сестрой Эда, она не может быть его женой, поэтому впишите «НЕТ» в ячейку матрицы Джоан—Эд. Пропустите на время следующие два предложения и остановитесь на фразе, что Эд весит больше мужа Викки. Это

415

значит, что Эд не является мужем Викки. Эд должен быть женат на Салли. Матрица принимает вид:

Перечитайте задачу и попробуйте найти еще ключи к решению. Нашли что-нибудь важное? Фред живет в Энн-Эрбор, а Джоан живет в Детройте; следовательно, можно предположить, что они не являются мужем и женой. Поскольку Фред не женат на Джоан и Салли, он должен быть мужем Викки. Кто же остается для Теда? Женой Теда должна быть Джоан.

Заполненная матрица выглядит так:

Возьмем еще один пример. Эта задача взята из прекрасной книги Филлипса (Phillips, 1961) под названием «Мои любимые загадки и головоломки». Наверное, она вам покажется проще, так как вы уже познакомились с техникой решения:

«Все мои четыре внучки — высокообразованные девушки», — заявил Кен Чезабл с явным удовольствием. «Каждая из них, — продолжил он, — играет на каком-нибудь музыкальном инструменте и говорит на одном из европейских языков, причем так же хорошо, если не лучше, как человек, для которого этот язык родной».

«На чем играет Мэри?» — спросил кто-то.

«На виолончели».

«А кто играет на скрипке?»

«Понимаете, — сказал Чезабл, — я постоянно забываю. О Господи, увы! Но я знаю, что это как раз та, которая говорит по-французски».

Кроме этого, мне удалось выудить из Кена только отрицания. Я узнал, что девушку, которая играет на органе, зовут не Валерия; ту, которая говорит по-немецки, зовут не Лорна; и что Мэри не знает итальянского. Антея не играет на скрипке и не говорит по-испански. Валерия не знает французского; Лорна не играет на арфе, а та, что играет на органе, не говорит по-итальянски.

На чем играет и какой язык знает Валерия?

Теперь остановитесь и поразмышляйте над этой задачей. Не продолжайте, пока действительно не продумаете ее.

Вам следует начать с осознания того, что исходная информация делится на категории, вследствие чего самым удобным представлением условий задачи будет матрица. Имеются четыре внучки, четыре музыкальных инструмента и четыре языка. Можно построить такую матрицу:

416

Поскольку большая часть информации дана в форме отрицания, давайте перечислим возможные комбинации внучек—инструментов—языков.

Так как девушка, которая играет на скрипке, говорит по-французски, она должна быть Лорной. Антея играет на органе и говорит по-немецки. Это означает, что только Мэри может говорить по-испански. А для Валерии остается единственная комбинация — арфа и итальянский.

Естественно, это искусственные задачи, непохожие на те, с которыми нам приходится сталкиваться в жизни. Давайте рассмотрим более практическое применение матричной формы представления задачи.

Существуют значительные разногласия во мнениях относительно применения витамина С как средства, сдерживающего распространение простуды Как бы вы решили этот вопрос: предотвращает или нет витамин С простуду? Вероятнее всего, вы бы дали витамин С некоторым людям и не дали бы другим, а затем подсчитали бы количество заболевших простудным заболеванием в каждой группе. Предположим, вы получили следующие результаты. 10 человек принимали витамин С и не заболели, 4 человека принимали витамин С и все-таки простудились, 8 человек, не принимавших витамин С, не заболели, а 6 человек, которые не принимали его, заболели. Какой вывод вы сделаете?

Поскольку исходная информация может быть разбита на категории (принимали или не принимали витамин С, простудились или нет), матрица, содержащая соответствующие значения, поможет нам правильно представить данные:

Изучая каждую ячейку матрицы, вы можете установить, предотвращает ли витамин С простуду. Чтобы оценить действие витамина, вам нужно посмотреть, сколько человек из числа простудившихся принимали его. Их число составляет 4 из 10, или 40%. А теперь оцените количество людей, не заболевших и принимавших витамин С. Как можно заметить, их 8 из 18; т.е. 55,5%. Из этого факта можно сделать вывод, что витамин С помогает предотвратить простуду. (Принципы исследований более подробно рассматриваются в главах 6 и 7.) Целью этого примера было показать, что матричное представление условий задачи облегчает поиски ответа. По

417

существу, это та же задача, что была рассмотрена в главе 8, когда врачи и медсестры должны были решить, существует ли связь между заболеванием и целым комплексом симптомов. Темы различных глав пересекаются, и вы должны представлять, что приемы, которые использовались в одной ситуации, могут также применяться в других, связанных с ней ситуациях

Используйте модели

Часто бывает удобно представить абстрактную задачу в конкретной форме. Я уверена, что вы видели когда-нибудь макеты планируемых архитектурных построек — таких, как торговый центр, офисы, студенческий городок. Макеты небольших строений и тротуаров не делаются — архитекторы любят грандиозные постройки. Часто такие макеты строятся для согласования планов будущего строительства с другими специалистами, которые не умеют читать чертежи, и в этом случае небольшие модели помогают решить задачу. Составленный из заменяемых деталей макет позволяет архитектору варьировать конструкцию и искать наилучший вариант расположения частей.

Давайте возьмем задачу, найти решение которой поможет создание модели. На мифической планете отдаленной галактики обитают два вида разумных существ — хоббиты и орки. Однажды три хоббита, увлекшись исследованием страны орков, потерялись. Хоббиты могли бы спокойно вернуться домой, если бы сумели перебраться через реку, отделяющую их страну от страны орков. Три орка согласились помочь хоббитам переправиться через реку, но единственная имеющаяся у них лодка могла выдержать только двоих — чего хоббиты никак не могли допустить, так как, обладая численным превосходством, орки могли в любой момент съесть их.

Ваша задача состоит в том, чтобы установить последовательность переправ, которая позволит трем хоббитам перебраться на другой берег реки, а трем оркам — вернуться на свой родной берег. Ограничением в этой задаче является то, что в лодке одновременно могут находиться только двое. К тому же если в какой-то момент времени число орков на берегу будет превышать число хоббитов, то вы должны будете отказаться от этого варианта и начать сначала.

Без наглядной формы представления этой задачи она кажется неразрешимой. Воспользуйтесь любыми маленькими предметами, которые будут заменять вам орков и хоббитов, и перемещайте их через воображаемую реку. Подойдут, например, три больших кусочка бумаги в качестве хоббитов, а три маленьких — в качестве орков. Вам надо будет представить, что вы перемещаете инопланетян в лодке. Не забывайте записывать все ваши ходы. Постарайтесь найти решение этой задачи в течение 10-15 минут. Занимаясь поиском решения, продумывайте каждый шаг. Не-продолжайте чтения, пока не решите эту задачу.

Последовательность всех необходимых действий для переправы хоббитов приведена на рис. 9.10. Одна из наибольших сложностей этой задачи заключается в необходимости переправить всех трех орков через реку — действия, которые сами по себе нежелательны, но которых нельзя избежать, чтобы не допустить численного превосходства орков над хоббитами. Задачи такого типа называют задачами с обходным маневром, поскольку пути их решения не прямолинейны. Нужны проме-

418

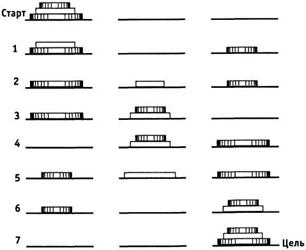
Рис. 9.10.Последовательность переправы трех хоббитов через реку на лодке, которая

одновременно может выдержать только двоих. При этом количество орков никогда не

превышает количество хоббитов.

жуточные шаги, которые, на первый взгляд, даже уводят от цели — в данном случае это переправа всех трех орков на противоположный берег реки, в то время как конечной целью, поставленной в задаче, является нахождение орков на их родном берегу. Очень важно осознать, что путь к намеченной цели может оказаться обходным. В качестве более приближенного к жизни примера рассмотрим стремление Леона стать очень обеспеченным человеком. Один из путей достижения этой цели — влезть в долги, чтобы оплатить образование. Хотя одалживание крупной суммы денег, на первый взгляд, уводит от намеченной цели разбогатеть, оно может оказаться необходимым обходным маневром для ее достижения. Когда вы столкнетесь со сложной задачей, будьте готовы рассмотреть и обходные пути ее решения.

419

Выберите лучшее представление

Использовать наглядные формы представления задачи (например, с помощью карандаша и бумаги) полезно в любом случае, когда у вас есть данные, которыми нужно оперировать. Ваша кратковременная память может быстро переполниться. Если вы уже прочитали главу 8, то должны осознавать, насколько важно снижение нагрузки на кратковременную память. Один из способов сделать это — выписывать возможные варианты путей решения и затем поочередно рассматривать их. Практически все данные, выраженные в числах — включая полученные в ходе эксперимента результаты, — следует всегда изображать графически. Если задача математическая или пространственная, то, вероятно, будет полезно применение диаграмм. Диаграмма сможет помочь распутать ситуацию, когда исходные данные взаимозависимы. Кроме того, диаграммы могут выделить некоторые важные отношения, которые нередко приводят непосредственно к цели. Иерархические деревья являются естественной формой представления задач, когда материал сам по себе образует иерархическую структуру. Матрицы чаще всего удобны, когда исходные данные могут быть разбиты на категории для последующего анализа. Модели хороши при представлении задач, решение которых определяет перемещение или передвижение данных. Часто именно выбор наглядного представления задачи является главным моментом, и от него зависит возможность решения задачи (Posner, 1973). Если вы обнаружите, что один из видов наглядного представления не помогает, попробуйте другой.

Стратегии решения задач

Решение задач может быть отнесено к наиболее характерной деятельности человека.

Полья (Ро1уа, 1962)

Глупо советовать человеку, столкнувшемуся с задачей, спланировать ее решение, если он понятия не имеет, как это делается. Казалось бы, что тут сложного? Нужно только разрабатывать одно за другим возможные решения и затем проверять их. А что если вы не можете придумать ни одного решения? Существует несколько стратегий, которые при правильном использовании могут помочь вам генерировать решения. Несмотря на то что ни одна отдельно взятая стратегия не может гарантировать вам универсальных решений на все случаи жизни, умение применять эти стратегии придаст направленность и уверенность вашим действиям при решении новых задач.

Шонфелд (Shoenfeld, 1979) заметил, что многие математики и ученые при решении стоящих перед ними задач прибегают к определенным стратегиям и правилам. Многие из них уверены, что если бы студенты приобрели некоторые базовые навыки, они бы решали задачи с большим успехом. Кроме того, исследователи обнаружили, что обучение, направленное на приобретение соответствующих навыков, может повысить способность человека решать возникающие задачи (напр., Klein, Weizenfeld 1978; Wickelgren, 1974). Приведенные ниже стратегии или руководства по решению задач можно рассматривать как способы планирования решения. (420:)

Анализ целей и средств

Чаще всего продвижение к цели не происходит по прямой вымощенной дороге. Если цель не может быть достигнута сразу, нередко приходится идти обходными путями или разбивать задачу на более мелкие части — так называемые подзадачи, каждая из которых имеет свою цель, или подцель.

Как и большинство стратегий решения задач, выбор и использование подцелей требует планирования. Процедура, согласно которой люди определяют подцели и используют их достижение для продвижения к основной цели, называется анализом целей и средств. Он является одним из основных, очень мощных средств решения задач. Сначала задача делится на подцели. Затем человек начинает действовать, чтобы достигнуть определенной подцели. Таким образом, с каждой отдельной победой он будет все ближе и ближе подходить к главной цели. Чтобы эта идея стала более понятной, давайте обратимся к примерам.

Первым шагом в анализе целей и средств является перечисление целей, которые можно поставить в данной задаче, и выбор наиболее перспективной из них. Предположим, что во время игры в шахматы вы поставили перед собой удачную подцель — поставить шах королю противника. Целью, естественно, является победа в игре, но для того, чтобы ее достичь, необходимо постоянно двигаться в направлении подцелей. Шах королю противника — это та ближайшая цель, в направлении которой вы продвигаетесь. Теперь вам необходимо выбрать средства для достижения данной цели — отсюда и термин анализ целей и средств. Чтобы достичь поставленной подцели, определите, какова текущая позиция ваших фигур. Затем определите разницу между той позицией, которую они занимают, и той, которой вы бы хотели достичь. Вам следует выбирать ходы, которые будут уменьшать эту разницу и позволят поставить шах королю противника. Предположим, этого нельзя добиться за один ход, тогда анализ целей и средств следует применить снова, на этот раз выбрав менее крупную подцель — возможно, это будет просто отдельный ход, направленный против какой-либо фигуры противника. Постоянное повторение этих двух процессов — выбора подцелей и сокращения расстояния до них — позволит вам продвигаться в направлении главной цели.

Любимая задача психологов, которая может служить демонстрацией анализа целей и средств, — это задача Ханойской башни. Название этой головоломке дала одна интересная легенда. Предположим, что имеются три колышка и 64 диска, каждый из которых имеет свой диаметр. Все диски нанизаны на один из колышков в порядке убывания диаметра. Для кого-то может быть удобнее представить диски в виде 64 пышек различных размеров, нанизанных одна за другой на колышек. Задача состоит в том, чтобы переместить диски с первого колышка на третий, используя средний для промежуточных действий. Правила переноса дисков заключаются в следующем: можно переносить только один диск за один раз и нельзя ставить больший диск на меньший. Легенда, связанная с задачей, гласит, что в одном монастыре вблизи Ханоя монахи заняты решением этой головоломки, а когда они закончат, настанет конец света. Даже если бы легенда оказалась правдой, у вас нет повода для беспокойства, поскольку, для того чтобы выполнить это задание, монахам понадобится примерно один триллион лет, если при этом они будут делать один ход в секунду. (421:)

Поскольку вы вряд ли собираетесь потратить столько времени на решение задачи Ханойской башни, вы можете попробовать решить ее упрощенную версию, используя только три диска. Вы легко можете приступить к решению, воспользовавшись тремя монетами различного диаметра (хорошо подойдут для этого монеты в 5 рублей, 2 рубля и 1 рубль) и тремя небольшими листочками бумаги. Сложите монеты пирамидкой на один лист бумаги так, чтобы монета наибольшего диаметра оказалась внизу, а наименьшего — наверху. Задача состоит в том, чтобы переместить монеты с первого листа бумаги на третий — при этом они должны быть расположены в том же порядке. За один прием можно брать только одну монету. Для решения задачи могут быть использованы все три листка бумаги. Записывайте все шаги, которые вы предпринимаете для решения этой задачи. Начальное и конечное положение монет показано на рис. 9.11.

Рис. 9.11.Начальное и конечное положение монет в задаче Ханойской башни. Для решения этой задачи используйте стратегию анализа целей и средств

При анализе целей и средств задачи Ханойской башни определяется одна из очевидных подцелей — положить самую большую по диаметру монету в 5 рублей на третий лист бумаги. Этого нельзя сделать сразу, так как на ней лежат монеты в 2 рубля и 1 рубль — следовательно, надо рассмотреть вторую подцель. Она заклю-

Рис. 9.12.Решение задачи Ханойской башни.

Обратите внимание, как достижение поставленных подцелей обеспечивает продвижение к основной цели

422

чается в создании ситуации, когда двухрублевая монета лежит на пятирублевой. Эта подцель будет достигнута, если монета в 1 рубль будет лежать на втором листе бумаги, а монета в 5 рублей на третьем. Эта подцель не может быть достигнута, поскольку первым можно перемещать только рубль. Таким образом, последовательно рассматриваются подцели, определяющие конец каждого этапа, и действия, направленные на их достижение. Окончательное решение со всеми необходимыми ходами показано на рис. 9.12. Если вы попробуете решить эту задачу не с тремя монетами, а с четырьмя или пятью, то убедитесь, что она значительно усложнится, хотя стратегия решения останется прежней.

Решение с конца

Анализ целей и средств является примером прямой стратегии — все планируемые действия ориентированы на приближение к подцели и, в конечном итоге, к основной цели. Иногда полезнее оказывается стратегия планирования операций решения с конца, которые обеспечивают движение от конечной цели назад — к текущему или исходному положению. Простейшим примером такой стратегии может служить игра в обожаемые детьми лабиринты, нарисованные ла бумаге, которые нужно проходить с помощью карандаша.

Многие из этих лабиринтов содержат несколько возможных путей, отходящих от начальной точки, и среди них только один верный путь, который приведет в конец лабиринта к заветной цели. Даже маленькие дети понимают, что они смогут ускорить решение такой задачки-лабиринта, если пойдут в обратном направлении, начав движение с конечной точки и прорисовывая путь к началу лабиринта. Пример такого лабиринта приведен на рис. 9.13.

Стратегия решения с конца очень удобна, если от конечной цели ведет меньше путей, чем из исходного положения. Разумеется, эта стратегия может быть применена не только для прохождения лабиринтов. Рассмотрим такую задачу: «Площадь, которую покрывают водяные лилии на одном из озер, удваивается каждые двадцать четыре часа. С того момента, как появилась первая лилия, до того, когда лилии полностью покрыли поверхность озера, прошло шестьдесят дней. Когда озеро было покрыто наполовину?» (Fixx, 1978, р. 50).

Единственным путем решения этой задачи является применение стратегии решения с конца. Можете ли вы решить ее, пользуясь этой подсказкой? Если озеро полностью было покрыто лилиями на 60-й день, а площадь, которую покрывают лилии, удваивалась каждые сутки, какая часть озера была закрыта в 59-й день? Ответ: половина. Таким образом, пользуясь обратным ходом, мы легко решили эту задачу. Прямая стратегия решения этой задачи наверняка завела бы нас в тупик.

Иногда оказывается эффективной комбинация прямой стратегии и стратегии решения с конца. Если вы столкнулись с геометрической или тригонометрической задачей на доказательство, то, вполне вероятно, прибегнув к комбинации этих двух стратегий, вы успешно с ней справитесь. Вы можете начать с конечного выражения, преобразуя его до какой-то определенной стадии, затем последовательно переходить от преобразования этого выражения к преобразованию исходного выражения и наоборот — до тех пор, пока они не совпадут на каком-то промежуточном этапе.

423

Рис. 9.13.Стратегия решения с конца удобна, когда из конечной точки ведет меньше путей, чем из исходного положения.

Упрощение

Вы все обдумываете и обдумываете свою задачу; попробуйте упростить ее. ...Довели ли вы ее до максимально возможного упрощения, до той ясности, которая наталкивает на мысли?

Полья (Ро1уа, 1962)

Задачи, вызывающие затруднения при решении чаще всего сложны по структуре. Хороший способ справиться с такой задачей — это упростить ее настолько, насколько возможно. Нередко удачно выбранная форма наглядного представления

424

задачи сама способствует ее упрощению, поскольку позволяет «увидеть» эффективный путь решения.

Предположим, вы столкнулись с классической задачей «кошка на дереве». Согласно устоявшемуся мнению, кошки могут карабкаться вверх по деревьям, но не могут спускаться. (На самом деле в этом утверждении не больше правды, чем в том, что слоны боятся мышей.) Предположим, вам надо снять кошку с ветки, расположенной на высоте 10 футов. В вашем распоряжении имеется единственная лестница длиной 6 футов. Для того чтобы лестница была надежно установлена, ее основание должно находиться на расстоянии трех футов от ствола. Дотянетесь ли вы до кошки?

Лучший путь к решению этой (и не только этой) задачи — графически изобразить исходные данные. Условия задачи графически показаны на рис. 9.14. Как только информация представлена в виде чертежа, ее можно воспринимать как простую геометрическую задачу: найти гипотенузу прямоугольного треугольника, если его катеты равны 10 и 3 футам. Такая формулировка задачи предполагает, что вы воспользуетесь своими знаниями о том, как вычисляются длины сторон треугольников. Факт остается фактом: когда для решения задачи требуется определенный уровень образования — его ничем не заменишь.

Рис. 9.14. Задача «кошка на дереве».

Если исходные данные представить в виде рисунка, задача превращается в простую геометрическую задачу.

425

Формула для нахождения гипотенузы треугольника имеет вид:

а² + Ь² = с².