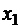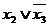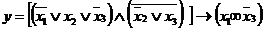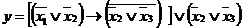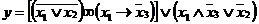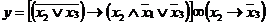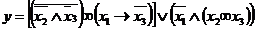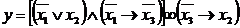Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Логічні функції двох зміннихСтр 1 из 2Следующая ⇒ Основи теорії множин Множина - це деякий набір об’єктів, які не повторюються і називаються елементами. Вона позначається в такий спосіб
де Будь який набір, кожний елемент якого належить множині Якщо Якщо серед предметів, що входять у сукупність Множину, яка складається з кінцевого числа елементів, має кінцеву потужність, називають кінцевою, множину, що не є кінцевою, називають нескінченною. Над множинами можливо виконувати такі дії. Рівність множин. Множини
Рівність множин
Рис. 1. Рівність множин
Об’єднання множин. Об’єднанням або сумою двох множин
Рис. 2. Об’єднання множин
Як правило виконуються наступні закони [1]: 1. Асоціативний
2. Комутативний
Перетинання множин. Перетинання двох множин називається множина, що складається із усіх тих елементів, які належать обом множинам (рис. 3). Для цієї операції використовується комутативний і асоціативний закони.
Рис. 3 Перетинання множин.
Дві множини Різниця множин. Різниця 
читається „ Рис. 4. Різниця множин
Доповнення множин. Доповнення множини
Рис. 5. Доповнення множин.
Індивідуальне завдання. Спростити множини.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Графи. Дії над ними
Граф є сукупність вершин, які мають відображення одна на другу. Він може бути заданий графічно (рис. 2.1), аналітично чи таблично (наприклад, з допомогою матриці суміжності).
Рис.2.1. Аналітично граф задається множинами вершин:
та відображеннями кожної вершини графа (рис 2.1):
Матричний засіб зображення графів використовується при обробці їх на ЕОМ. Матрицею суміжності називається квадратна матриця
Над графами можливо виконувати слідуючи основні дії: 1. Об’єднанням графів є новий граф, вершини якого є об’єднанням множин вершин першого і другого графів, а відображення кожної вершини нового графа є об’єднання відображень цієї вершини на першому і другому графах:
Наприклад надані два графа (ріс. 2.2 і 2.3) Рис. 2.2 Рис. 2.3
Граф рис. 2.4 є об’єднання графів рис. 2.2 і 2.3
Рис. 2.4 2. Перетинання графів – це новий граф
вершини якого є перетинання вершин першого і другого графів
а відображення кожної вершини нового графа є перетинання відображень цієї вершини на першому і другому графах
Для рис. 2.2 і 2.3
Граф рис. 2.5 є перетинання початкових графів
Рис. 2.5 3. Декоративний добуток графів є добуток матриць суміжності Граф рис. 2.2 можливо зобразити матрицею
а рис. 2.3 матрицею Кожний елемент матриці Графічно декартовий добуток можливо показати на рис. 2.6:
Рис. 2.6 4. Сума графів виконується з використанням матричного рівняння:
де Для розглянутого вище прикладу:
Отримана регулярна клітиночна матриця, яка побудована з 4 видів кліток. Якщо елемент матриці
Якщо
0 Рис. 2.7
Індивідуальне завдання. Знайти декартовий добуток і суму графів, заданих матрицями суміжності. Варіант 1 Варіант 2 Варіант 3 Варіант 4 Варіант 5 Варіант 6 Варіант 7 Варіант 8 Варіант 9 Варіант 10 Варіант 11 Варіант 12 Варіант 13 Варіант 14
Варіант 15 Варіант 16 Варіант 17 Варіант 18 Варіант 19 Варіант 20 Варіант 21 Варіант 22 Варіант 23 Варіант 24 Варіант 25
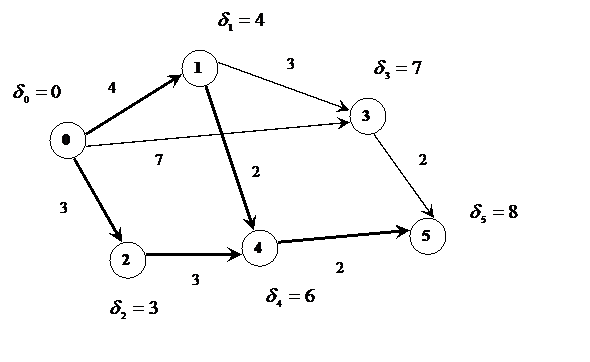
Варіант 26 Варіант 27 Варіант 28 При оптимізації технологічних процесів з допомогою графів знаходять як найкоротший шлях на графі. Це можливо зробить з допомогою машинного алгоритму Дейкстри. Розглянемо цей алгоритм на прикладі. Наданий орієнтований граф (рис. 2.8).
Рис. 2.8
Присвоїмо навчальній вершині графа постійну мітку Знаходимо нові тимчасові мітки вершини 1,2,3 по формулі:
де Нові оцінки цих вершин
Вершини з найменшою оцінкою присвоюється постійна мітка
Далі по формулі (2.9) знаходимо нову мітку вершини 4:
найменшу тимчасову мітку має вершина 1. Присвоюємо їй постійну мітку По формулі (2.9) знаходимо нові мітки вершин 3 і 4, в які входять дуги з вершин з постійними мітками:
Вершині 4 присвоюємо постійну мітку
Найменшу тимчасову мітку має вершина графа 3. Їй присвоюємо постійну мітку Тоді
Індивідуальне завдання У таблицях 1-5 наведені вартість купівлі устаткування та підтримання його у робочому стані з урахуванням інфляції та його модернізації. Заміна устаткування може бути зроблена не раніше чим через 4 роки. Розглядаємо період експлуатації 5-9 років (для різних варіантів). Знайти найкращу стратегію зміни та підтримки устаткування у робочому стан, при якої сумарні витрати будуть найменшими
Таблиця 1
Таблиця 3
Таблиця 4
Таблиця 5
Логічні функції двох змінних Логіка – наука про форми та закони мислення. Математична логіка використовує математичні методи та спеціальний апарат символів для рішення логічних задач. У цьому розділі дискретної математики особливу роль будуть грати двійкові елементні множини і двійкові змінні. Ці елементи позначають Ø і 1, проте вони не є числами в звичайному значенні. Алгебра, утворена множиною разом із усіма можливими операціями на ньому, називається алгеброю логіки. Логічною функцією від Таблиця істинності логічних функцій двох змінних.
1.Закон переміщення:
2.Закон сполучення:
3.Розподільний:
Всі закони логіки можливо доказати за допомогою таблиці 1: Із розподільного закону для кон’юнкція можна зробити два слідства: – правило зникнювання
– правило поглощение
ці правила використовуються прі мінімізації логіческих функцій. 4.Закон інверсії (правило де-Моргана)
В алгебрі логіки використовуються наступні логічні тождества:
Приклади рішення завдань 3.1. Спростити логічне вираження
Рішення. Замінимо операцію імплікації найпростішими логічними функціями (диз'юнкція, конъюнкция, заперечення) на підставі таблиці 2
Звільнимося від заперечення над комплексом перемінних
3.2. Логічна функція задана аналітично
Задати неї за допомогою таблиці істинності. Рішення. Перетворимо дане логічне рівняння в СКНФ, додаючи до неповних співмножників 0 у виді тотожності
На підставі отриманого рівняння складемо таблицю істинності. Нуль “y” приймає в чотирьох стовпчиках (крапках логічного простору) по числу співмножників у правій частині отриманого рівняння ,причому аргументові без заперечення відповідає 0,із запереченням – 1 у шуканому стовпці. В інших стовпцях “y” приймає щире (одиничне) значення. 3.3. Мінімізувати логічне рівняння
Рішення. Для мінімізації цього рівняння використовуємо метод Квайна (правило склеювання). Мінімізуємо доданки візьмемо в квадратні дужки, повтор двічі доданок
Для мінімізації цього рівняння можна використовувати діаграму Вейча.
Об'єднати “одиниці” у діаграмі можна іншим способом (табл.5).
При цьому
3.4. Мінімізувати логічне рівняння
Рішення. Для мінімізації конъюнктивних норрісьних форм використовуємо співвідношення, що випливає з розподільного закону для диз'юнкції Мінімізирувані співмножники об'єднаємо в квадратні дужки, дописавши співмножник
Для мінімізації заданого рівняння можна використовувати діаграму Вейча.
Таблиця 6.
Індивідуальне завдання. Преобразовати
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 187. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 - множина,
- множина,  - її елементи .
- її елементи . має свою підмножину
має свою підмножину 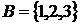 , та позначається
, та позначається  .
. , то кажуть, що
, то кажуть, що  рівні тоді, коли кожний елемент множини
рівні тоді, коли кожний елемент множини 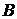 , і навпаки, кожний елемент множини
, і навпаки, кожний елемент множини 



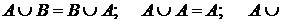 Ø
Ø 

 якщо
якщо 
 .
. Ø
Ø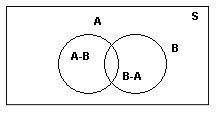

 ”
”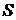 , крім тих, що належать множені
, крім тих, що належать множені  (рис. 5)
(рис. 5)
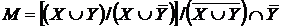


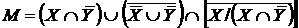

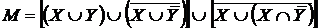








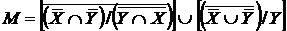


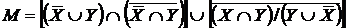











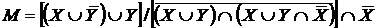 .
.

 ;
; 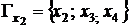 ;
;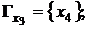
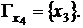
 , де
, де  - кількість вершин графа. У цієї матриці
- кількість вершин графа. У цієї матриці 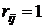 , якщо вершина
, якщо вершина  суміжна з вершиною
суміжна з вершиною  , тобто має відображення на цю вершину. Якщо вершина
, тобто має відображення на цю вершину. Якщо вершина 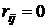 . Для рис 2.1
. Для рис 2.1 .
.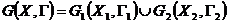 (2.1)
(2.1) (2.2)
(2.2)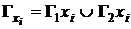 (2.3)
(2.3)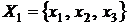
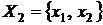
 .
.


 Ø =
Ø = 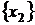

 (2.4)
(2.4)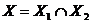 (2.5)
(2.5) (2.6)
(2.6)

 Ø
Ø
 і
і  початкових графів.
початкових графів. ,
, . Тоді матриця суміжності нового графа
. Тоді матриця суміжності нового графа

 , (2.8)
, (2.8) - одиничні матриці розмірністю матриць
- одиничні матриці розмірністю матриць  .
. , то відповідна клітка матриці
, то відповідна клітка матриці  дорівнює
дорівнює
 не знаходиться на головній діагоналі
не знаходиться на головній діагоналі

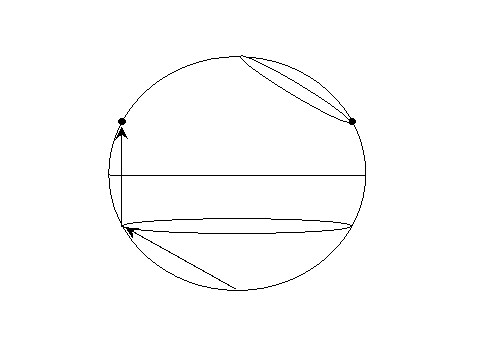
 Графічно сума графів для наведеного прикладу буде виглядати рис. 2.7
Графічно сума графів для наведеного прикладу буде виглядати рис. 2.7
 .
. .
. .
.
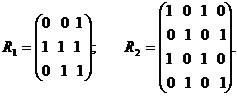

 .
.













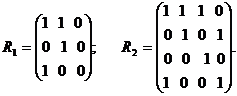






 , останні вершини мають тимчасові мітки
, останні вершини мають тимчасові мітки 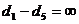 .
. , (2.9)
, (2.9) означає, що вершина
означає, що вершина  є попередньою для вершини
є попередньою для вершини  ;
;  - оцінка дуги
- оцінка дуги  .
. ,
,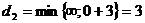 ,
, .
. .
.
 .
. ,
, .
. По формулі (2.9):
По формулі (2.9): .
.
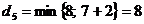 , це є її постійна мітка
, це є її постійна мітка  Це є довжина найкоротшого шляху графа. Таких шляха 2: 0-1-4-5 або 0-2-4-5.
Це є довжина найкоротшого шляху графа. Таких шляха 2: 0-1-4-5 або 0-2-4-5. :
:
 Таблиця 2
Таблиця 2

 змінних називається
змінних називається 


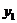

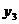
 2
2

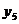
















 .
.


 .
.

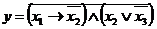
 .
.
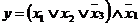 .
. .
.



 .
.

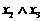

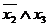
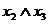


 1
1
 1
1

 .
.