
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вторая формула среднего значения.Производная частного от деления двух функций
5. Дифференциал функции-линейная относительно Δх часть приращения функции. Она обозначается какdy или df(х). Таким образом: Дифференциал сложной функции: df(x)= f ¢(x)dx 6.Обозначения: Частной производной функции z=f(x,y) в точке (x0, y0)
7.Пусть задана функция z = f(х, у). Так как х и у – независимые переменные, то одна из них может изменяться, а другая сохранять постоянное значение. Дадим переменной х приращение ∆х, сохраняя значение переменной у неизменным. Тогда функция zполучит приращение, которое назовем частным приращением z по х и обозначим ∆х z: ∆х z = f(x + ∆x, y) – f(х, у). Аналогично получаем частное приращение z по у: ∆у z = f(x, у + ∆ y) – f(х, у). Наконец, если аргументу х дать приращение ∆х, а аргументу у – приращение ∆у, то получим полное приращениефункции z: ∆ z=f(x+∆x, y+∆у)–f(х, у). Надо заметить, что полное приращение функции, вообще говоря, не равно сумме частных её приращений, т.е. ∆z ≠ ∆хz + ∆у z. 8.Дифференциал функции u=f(y;х) найденный при условии, что один из ее аргументов рассматривается как переменная величина, а остальные – постоянные величины, называется частным дифференциалом по соответствующей переменной. То есть по определению, частные дифференциалы по переменным х,y соответственно равны (везде без z) 
9.
10. Первообразная данной функции {\displaystyle f(x)}f(x) называют такую {\displaystyle F(x)}F(x), производная которой (на всей области определения) равна {\displaystyle f}f, то есть {\displaystyle F'(x)=f(x)}F́ (x)=f(x). Вычисление первообразной заключается в нахождении неопределённого интеграла. 11.Неопределенным интегралом от функции f(x) на интервале (a,b) называется совокупность всех первообразных функции f(x) на этом интервале ò f (x)dx = F(x)+C, где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, x – переменная интегрирования. 12, 13, 14,15.
16. Первая формула среднего значения. Пусть функция y = f(x) интегрируема на отрезке [a; b], Следствие.Если функция y = f(x) непрерывна на отрезке [a; b], то найдется такое число Первая формула среднего значения в обобщенной форме. Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке [a; b], Вторая формула среднего значения. Если на отрезке [a; b] функция y = f(x) интегрируема, а y = g(x) монотонна, то существует такое число
17. Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком производной или дифференциала. Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным (сокращенно ОДУ – обыкновенное дифференциальное уравнение). Если же неизвестная функция есть функция многих переменных, то дифференциальное уравнение называют уравнением в частных производных. Максимальный порядок производной неизвестной функции, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения. 18. Дифференциальное уравнение первого порядка y′=f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y: f(x,y)=p(x)h(y),где p(x) и h(y) − непрерывные функции. 19.Если решение дифференциального уравнения удовлетворяет изначально заданным дополнительным условиям, то его называют частным решением дифференциального уравнения.Общее решение дифференциального уравнения – это множество решений, содержащее все без исключения решения этого дифференциального уравнения. 20. Если Когда коэффициенты уравнения называют ЛОДУ с постоянными коэффициентами(если 21, 22,23. Рассмотрим линейное дифференциальное уравнение видаy′′+py′+qy=0,где p,q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:k2+pk+q=0.Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи: 1. Дискриминант характеристического квадратного уравнения положителен: D>0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функциейy(x)=C1ek1x+C2ek2x,где C1 и C2 − произвольные действительные числа. 2. Дискриминант характеристического квадратного уравнения равен нулю: D=0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:y(x)=(C1x+C2)ek1x. 3. Дискриминант характеристического квадратного уравнения отрицателен: D<0. Такое уравнение имеет комплексно-сопряженные корни k1=α+βi,k2=α−βi. Общее решение записывается в видеy(x)=eαx[C1cos(βx)+C2sin(βx)].
24. Испытание – осуществление некоторого определенного комплекса условий, который может быть повторен сколь угодное число раз.Результат, исход испытания называется событием.(Сдача экзамена - это испытание; получение определенной отметки - событие. Выстрел - это испытание; попадание в определенную область мишени - событие. Бросание игрального кубика - это испытание; появление того или иного числа очков на брошенной игральной кости - событие.) 25. Достоверное событие – событие, которое в результате испытания обязательно произойдет. Невозможное событие – событие, которое в результате испытания не может произойти. Случайное событие – событие, которое в результате испытания может произойти либо не произойти. 26.Два события называются совместными, если в результате одного испытания наступление одного из них исключает наступление второго.несовместными если никакие из них не могут появиться одновременно в результате однократного проведения эксперимента. 27.Случайные события образуют полную группу событий, если при каждом испытании может осуществиться событие только из этой группы и не может осуществиться любое несовместное ним.Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. 28. Согласно классическому определению вероятностью P(A) события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n всех элементарных (т.е. всех возможных, несовместных) исходов (образующих полную группу).Р(А)= 29.Усло́внаявероя́тность — вероятность наступления одного события при условии, что другое событие уже произошло. 30. Суммой событий А и В называется событие С, заключающееся в наступлении хотя бы одного из событий А и В. 31.Произведением событий А и В называется событие С, состоящее в одновременном наступлении событий. 32. Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных. События называются зависимыми, если одно из них влияет на вероятность появления другого.
33.Теорема сложения вероятностей Вероятность суммы двух событий А и В равна сумме вероятностей этих событий минус вероятность их совместного наступления.P(A+B)=P(A)+P(B)-P(AB) 34.Теорема умножения вероятностей Вероятность наступления события В, зависящая от наступления события А называется условной вероятностью события В. PA(B)=P(B/A) Два события называются независимыми, если вероятность осуществления одного из них не зависит от наступления другого.Вероятность произведения двух событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие произошло. P(AB)=P(A)P(B/A)= P(B)P(A/B) 35. полной вероятности позволяет вычислить вероятность интересующего события
36, 37. Формула Бернулли, Пуассона скину отдельно, не хотят вставляться. 38, 39. Скину ссылку на теорему, тоже не хочет вставляться. 40. Величину, которая в результате испытания примет одно и только одно возможное значение (при этом заранее не известно какое именно), называют случайной.Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. 41. Законом распределения ДСВ называется соответствие между её возможными значениями и их вероятностями. Закон распределения чаще всего задается в табличной форме. (помните табличку делали на самостоятельной работе, из двух строк со значениями х,р) воот, такая таблица называется рядом распределения. Для наглядности закон распределения ДСВ можно изобразить графически, для чего в прямоугольной системе координат строят точки (xi ,pi), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения (а это график, который мы строили по таблице) 43.Математическим ожиданием ДСВ X с конечным числом значений называется сумма произведений возможных ее значений на их вероятности.M(X) =μ= x1p1 + x2p2 +...+ xnpn = å=хipi(над сигмой должна стоять буква n, под сигмой i=1, в самой формуле 1 и 2 это индексы) 44.1. Математическое ожидание постоянной (неслучайной) величины С равно самой постоянной M(C) = C. 2. Математическое ожидание алгебраической суммы нескольких случайных величин равно алгебраической сумме математических ожиданий слагаемых M(X1 ± X2 ±...± Xn) = M(X1) ± M(X2) ±…± M(Xn). 3. Константу можно вынести за знак математического ожидания M(CX)=CM(X). 4. Математическое ожидание произведения нескольких независимых случайных величин равно произведению математических ожиданий этих величин M(X1X2...Xn) = M(X1)M(X2)...M(X)n. 45.Дисперсией ДСВ X называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания. 46.- 47. Свойства дисперсии. 1. Дисперсия постоянной величины равна нулю D(С) = 0. 2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(CX) = C 2D(X). 3. Дисперсия суммы (разности) двух независимых случайных величин равна сумме дисперсий этих величин: D(X±Y)=D(X)±D(Y). 48. Средним квадратическим отклонением случайной величины называют квадратный корень из её дисперсии. 49. Функцией распределения ДСВ (кумулятивной) называется функция F(X), равная вероятности события, в котором случайная величина Х приняла значение меньше х, F(X)=P(X<x). Свойства: 1. 0 £ F(X)£1 (из определения вероятности) 2. F(х) – неубывающая функция 3. Вероятность попадания случайной величины Х в полуинтервал [a,b) равна разности между значениями функции распределения в правом и левом концах интервала (a,b) P(a £ x < b) = F(b)- F(a) 4. Вероятность того, что случайная величина Х примет заранее заданное значение а равна нулю P(X= a) = 0 50.Мода дискретной случайной величины – это ее наиболее вероятное значение. 51, 52. Скину ссылку 53. – 54.Математическая статистика — раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений. 1) систематизировать полученный статистический материал; 2) на основании полученных экспериментальных данных оценить интересующие нас числовые характеристики наблюдаемой случайной величины; 3) определить число опытов, достаточное для получения достоверных результатов при минимальных ошибках измерения. 55.1) систематизировать полученный статистический материал; 2) на основании полученных экспериментальных данных оценить интересующие нас числовые характеристики наблюдаемой случайной величины; 3) определить число опытов, достаточное для получения достоверных результатов при минимальных ошибках измерения. 55.Относительная частота показывает, какая доля экспериментов завершилась наступлением данного исхода.Частота случайного события и «статистическое определение» вероятности называется частотой события А в данной серии испытаний. 56. ответ на этот вопрос в 41 57.Генеральная совокупность —совокупность всех объектов (единиц), относительно которых предполагается делать выводы при изучении конкретной задачи. выборочная совокупность — часть генеральнойсовокупности элементов, которая охватывается экспериментом (наблюдением, опросом). 58.Пусть Θ∗Θ∗ есть статистическая оценка неизвестного параметра ΘΘ теоретического распределения. Допустим, что по выборке объема nn найдена оценка Θ∗1Θ1∗ . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку Θ∗2Θ2∗ и т. д. Получим числа Θ∗1,Θ∗2,…,Θ∗kΘ1∗,Θ2∗,…,Θk∗ , которые будут различаться. Таким образом, оценку Θ∗Θ∗ можно рассматривать как случайную величину, а числа Θ∗1,Θ∗2,…,Θ∗kΘ1∗,Θ2∗,…,Θk∗ — как возможные ее значения.
Если оценка Θ∗Θ∗ дает приближенное значение ΘΘ с избытком, то найденное по данным выборок число Θ (k=1,2,…,n)Θ (k=1,2,…,n) будет больше истинного значения ΘΘ . Следовательно, и математическое ожидание (среднее значение) случайной величины Θ∗Θ∗ будет превышать ΘΘ , то есть M(Θ∗)>ΘM(Θ∗)>Θ . Если ΘΘ дает приближенное значение ΘΘ с недостатком, то M(Θ∗)<ΘM(Θ∗)<Θ .
Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Поэтому нужно потребовать, чтобы математическое ожидание оценки ΘΘ было равно оцениваемому параметру. Соблюдение требования M(Θ∗)=ΘM(Θ∗)=Θ устраняет систематические ошибки. 59.- 60. 61, 62,63. Надеюсь, они нам не попадутся. Не могу найти эти формулы
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 268. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


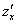 или
или  – частная производная по «икс»
– частная производная по «икс» или
или  – частная производная по «игрек»
– частная производная по «игрек» D(у) по соответствующей переменной называется предел отношения частного приращения функции по этой переменной к приращению этой переменной, когда приращение переменной стремится к нулю (если этот предел существует и конечен).
D(у) по соответствующей переменной называется предел отношения частного приращения функции по этой переменной к приращению этой переменной, когда приращение переменной стремится к нулю (если этот предел существует и конечен). ,
,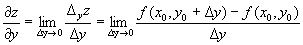 .
.




 и
и 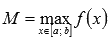 , тогда существует такое число
, тогда существует такое число  , что
, что  .
. , что
, что  .
. . Тогда существует такое число
. Тогда существует такое число  .
. .
. , то уравнение
, то уравнение  называют линейным однородным дифференциальным уравнением (ЛОДУ), в противном случае – линейным неоднородным дифференциальным уравнением (ЛНДУ).
называют линейным однородным дифференциальным уравнением (ЛОДУ), в противном случае – линейным неоднородным дифференциальным уравнением (ЛНДУ). являются постоянными функциями (то есть, некоторыми числами), то соответствующие дифференциальные
являются постоянными функциями (то есть, некоторыми числами), то соответствующие дифференциальные

 через вероятности его произойти при выполнении гипотез с заданной вероятностью. Формула полной вероятности требуется, когда необходимо узнать вероятность совершения некоторого события, если его совершение зависит от нескольких условий.
через вероятности его произойти при выполнении гипотез с заданной вероятностью. Формула полной вероятности требуется, когда необходимо узнать вероятность совершения некоторого события, если его совершение зависит от нескольких условий.

