
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Швидкість та прискорення гармонічних коливаньЛекція № 1. МЕХАНІЧНІ КОЛИВАННЯ Гармонічні коливання та їх характеристики Одним із типів руху механічних систем є малі коливання, які система виконує біля свого положення стійкої рівноваги. Коливаннями – називаються рухи або процеси, які повторюються у часі. Коливання бувають як механічні, так і електромагнітні. Однак, різні коливальні процеси описуються однаковими характеристиками та рівняннями. Системи, у яких можна спостерігати періодичний рух, називаються коливальними. Періодичний рух, що одного разу виник, може продовжуватися без дії зовнішніх періодичних сил. Коливання, що відбуваються в системі, на яку не діють зовнішні сили, називаються вільними. Вільні коливання відбуваються за рахунок початкової енергії, у відсутності зовнішніх впливів на коливальну систему в подальшому. Розглянемо ці рухи у найбільш простому випадку, коли система має усього лише один ступінь вільності. Це означає, що для однозначного визначення положення коливальної системи в просторі досить задати всього одне число. Це не обов'язково має бути декартова координата, а в залежності від умов задачі може виявитися більш зручним вибір якоїсь іншої величини. Така величина, що однозначно характеризує положення системи, називається її узагальненою координатою. Найпростішим типом коливання є гармонічні коливання, де залежність від часу задається рівнянням:
де А – амплітуда - максимальне значення коливної величини, w0 – циклічна частота, яка є основною характеристикою коливань, що не залежить від початкових умов руху, і зокрема, від енергії,  j0 – початкова фаза коливань при t=0, j = (w0t +j0)– фаза коливань у момент часу t. Фаза показує стан коливальної системи на даний момент часу. Певні стани системи повторюються через проміжок часу, який називається періодом коливань Т. Це час, за який фаза коливань збільшується на 2p:
Таким чином, період коливань Т – це проміжок часу, через який повторюються значення всіх фізичних величин, які характеризують коливання. Наприклад, якщо система виконує n коливаньза час t, то період Т знаходиться, як Період коливань у системі СІ виміряється в секундах [c]. Величина, обернена до періоду коливань називається частотою. Таким чином, частота це число коливань в одиницю часу. У системі СІ одиниця вимірювання частоти – Герц [Гц]
Якщо підставити (1.2) у (1.3), одержимо зв'язок циклічної частоти з частотою, а також і з періодом коливань:
Диференціальне рівняння вільних коливань Для вивчення будь-якого фізичного явища необхідна модель. Моделлю для вивчення коливань є гармонічний осцилятор. Гармонічним осцилятором називається коливальна система, коливання якої, може бути описаним диференційним рівнянням вільних гармонічних коливань, що має вигляд:
Вираз (1.5) є лінійним однорідним диференціальним рівнянням другого порядку. Відповідно до загальної теорії лінійних диференціальних рівнянь, розв’язком рівняння (1.5) є вираз (1.1). Прикладами гармонічного осцилятора є пружинний, математичний і фізичний маятники. Пружинний маятник
Пружинний маятник – тіло, підвішене на пружині жорсткістю k.Стан тіла у якому пружина не деформована – це стан стійкої рівноваги. При відхиленні тіла від положення рівноваги у результаті деформації виникає сила пружності, що, відповідно до закону Гука, дорівнює Вільні коливання відбуваються за рахунок початкової енергії, у відсутності зовнішніх впливів на коливальну систему в подальшому. У випадку пружинного маятника рівняння руху, відповідно до другого закону Ньютона, можна записати m або Врахувавши, що
Потенціальна енергія пружинного маятника визначається як:
Математичний маятник Математичним маятником називають підвішений на тонкій нерозтяжній нитці вантаж, розміри якого менші від довжини нитки, а маса більша за масу нитки. Положення, у якому нитка вертикальна – це положення стійкої рівноваги. У положенні стійкої рівноваги сила ваги mg зрівноважена силою натягу нитки Т. (див. рис.1.2). Якщо відхилити нитку на кут α – рівнодіюча сила ваги вантажу і натягу нитки буде спрямована в напрямку положення стійкої рівноваги.
Якщо тіло відпустити, ми будемо спостерігати вільні коливання. Під час коливань змінюється тільки координата х. Запишемо проекцію рівнодіючої сили на вісь х: Fх = Тх = - |Т|sina (1.10) При малих значенях a (a ~4о) нехтуємо рухом уздовж вертикальної вісі у.
Визначимо з рівняння (1.10) враховуючи (1.9) проекцію рівнодіючої сили на вісь х, яка, відповідно до другого закону Ньютона, дорівнює
Враховуючи, що
Рис. 1.2. Отримуємо ma=-mg звідки a=-g
Рівняння гармонічних коливань математичного маятника можна записати в диференціальній формі: Підставивши значення
де l – довжина математичного маятника. Фізичний маятник Фізичний маятник – тверде тіло, яке під дією сили ваги виконує коливання навколо нерухомої осі, яка не проходить через центр мас. Вісь обертання, фізичного маятника розташована вище від центра мас (рис.1.3). Обертальний момент, який виникає при коливанні фізичного маятника, дорівнює M=Jε= J де J – момент інерції, ε – кутове прискорення, l – відстань між точкою підвісу та центром мас. Рівняння (1.14) можна записати у вигляді J Звідси
Період коливань фізичного маятника :
де Зведена довжина фізичного маятника дорівнює довжині математичного маятника, які здійснюють коливання з однаковим періодом. Період коливань фізичного маятника, а отже, і його зведена довжина, залежать від відстані між точкою підвісу до центра мас маятника. Відповідно до теореми Штейнера, момент інерції визначається, як сума моменту інерції відносно центру мас та добутку маси на квадрат довжини від точки підвісу до центу мас. Тоді період коливань дорівнюватиме:
де J0 –момент інерції центру мас. На практиці значення низьких частот систем можуть бути малими. Наприклад, мотузка, яка підвішена на двох стовпах, може у випадку достатнього провисання виконувати вільні коливання з частотою 1-2 Гц. Коливання такого типу були виявлені восени 1959 р. у дротах лінії електромереж. Частота коливань була низькою біля 1,8 Гц. Дроти діаметром 43 мм, які були протягнуті над річкою, кріпилися до двох великих пилонів, відстань між якими була більше від 1,6 км. Коли дув вітер з невеликою силою і в потрібному напрямку, з’являлись інтенсивні низькочастотні коливання дротів, відстань між якими була 8,2 м, вони дотикалися один до одного, що викликало коротке замикання в електромережі. У подальшому, щоб уникнути цих коливань, дроти вкривали тонкою пластиковою стрічкою, при цьому змінювалась геометрія поверхні, що обтікалась повітряним потоком. Коливання дротів електромережі не є вільними коливаннями, оскільки система перебувала під дією зовнішнього джерела енергії – вітру. Для рішення цієї проблеми інженерам була потрібна інформація про значення власних частот системи, які близькі до частоти коливань дротів електромережі.
Швидкість та прискорення гармонічних коливань Якщо матеріальна точка виконує прямолінійні гармонічні коливання уздовж осі координат х біля положення рівноваги, яке приймається за початок координат, то залежність координати х від часу t описується рівнянням (1.1). Швидкість u та прискорення a точки коливань відповідно дорівнюють:
та Таким чином, маємо гармонічні коливання з тією ж циклічною частотою і амплітудами Аw0 –швидкості коливань, та Аw02 – прискорення коливань. Рівняння (1.17) і (1.18) можна представити у вигляді диференціального рівняння другого порядку, яке описане виразом (1.5). Фаза швидкості (1.17) відрізняється від фази (1.1) на Прискорення дорівнює нулю у тих випадках, коли коливна точка проходить положення рівноваги, а коли зміщення коливної точки дорівнює амплітудному значенню, то і прискорення має максимальне значення. Вектор прискорення завжди має напрямок у бік положення рівноваги. Віддаляючись від положення рівноваги, коливальна точка рухається сповільнено, наближуючись до нього – прискорено. Графік гармонійного коливання, описаного рівнянням (1.1), швидкості гармонічного коливання (1.17) та прискорення (1.18) показані на рис. 1.4. Видно, що зміщення, швидкість та прискорення коливної точки, є періодичними функціями від часу з однаковими періодами.
Енергія коливань Кінетична енергія матеріальної точки, яка виконує гармонічні коливання дорівнює:
Потенціальна енергія матеріальної точки, яка виконує гармонічні коливання під дією пружної сили дорівнює:
Підставляючи значення, одержуємо вираз для потенціальної енергії коливного тіла. Повна енергія, за законом збереження, залишається постійною. Склавши (1.19) і (1.20), одержимо формулу повної енергії:
Повна енергія залишається сталою, оскільки при гармонічних коливаннях виконується закон збереження механічної енергії, бо пружня сила консервативна. З (1.21) видно, що значення повної енергії залежить прямопропорційно від маси коливного тіла, а також від квадрату амплітуди.
|
||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 465. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (1.1)
, (1.1) (1.2)
(1.2)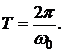
 .
. . (1.3)
. (1.3) . (1.4)
. (1.4) + ω2х . (1.5)
+ ω2х . (1.5)
 .
. 
 = - kx
= - kx  , одержимо рівняння (1.5). Беручи до уваги рівняння (1.4), знаходимо період коливань пружинного маятника, який визначається як
, одержимо рівняння (1.5). Беручи до уваги рівняння (1.4), знаходимо період коливань пружинного маятника, який визначається як . (1.7)
. (1.7) . (1.8)
. (1.8)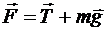 . (1.9)
. (1.9) (1.11)
(1.11)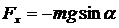 .
. 
 ,
, ,
,  одержимо рівняння (1.5) Звідси період коливань математичного маятника дорівнює:
одержимо рівняння (1.5) Звідси період коливань математичного маятника дорівнює: , (1.13)
, (1.13)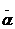 = Fτ ℓ = - mgℓsinα ≈ - mgℓα (1.14)
= Fτ ℓ = - mgℓsinα ≈ - mgℓα (1.14) або
або  .
.
 , (1.15)
, (1.15) – зведена довжина фізичного маятника.
– зведена довжина фізичного маятника. , (1.16)
, (1.16) , (1.17)
, (1.17) . (1.18)
. (1.18)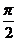 , а фаза прискорення (1.18) на
, а фаза прискорення (1.18) на  . У момент часу, коли х=0 швидкість коливної точки, має максимальне значення та дорівнює амплітуді швидкості у ті моменти коли коливна точка проходить через положення рівноваги. При максимальних зміщеннях від положення рівноваги (х =±А) швидкість дорівнює нулю.
. У момент часу, коли х=0 швидкість коливної точки, має максимальне значення та дорівнює амплітуді швидкості у ті моменти коли коливна точка проходить через положення рівноваги. При максимальних зміщеннях від положення рівноваги (х =±А) швидкість дорівнює нулю.





 . (1.19)
. (1.19) (1.20)
(1.20) . (1.21)
. (1.21)